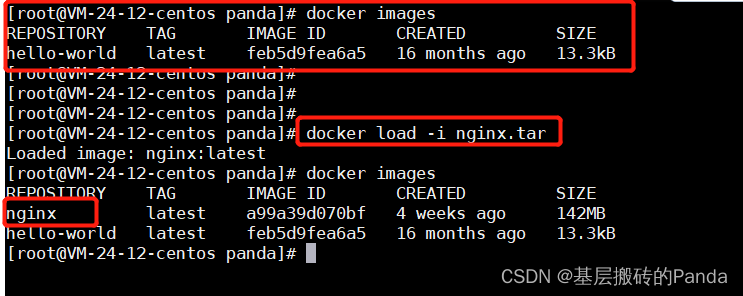
1,定义:
1,最大权闭合子图是最小割的一个模型。即每一个子图中的每一个点,其出边的点也全应该在这个子图中。而所有子图中,其点的权值和最大就是最大权闭合子图。
2,构建该图,我们把所有正权值点与源点s连接(其边权为点权),所有负权值点有汇点t连接(其边权为负点权(即改为正数)),而点与点之间的边都是INF的边。这样,我们的最小割一定割的是连接s或者t的边(最小割不会割INF边的)。
3,我们说过,点的出边一定要与点在同一个子图中,所以建立点与点之间的关系(如a->b,a->c),其关系为走a必须同时走b和c。
4,我们把所有正权值点加起来为sum,而我们走最小割时,就等于舍弃这个正权值边或者走了这个负权值边。
即最大权闭合子图答案为sum-最小割。
证明如图:
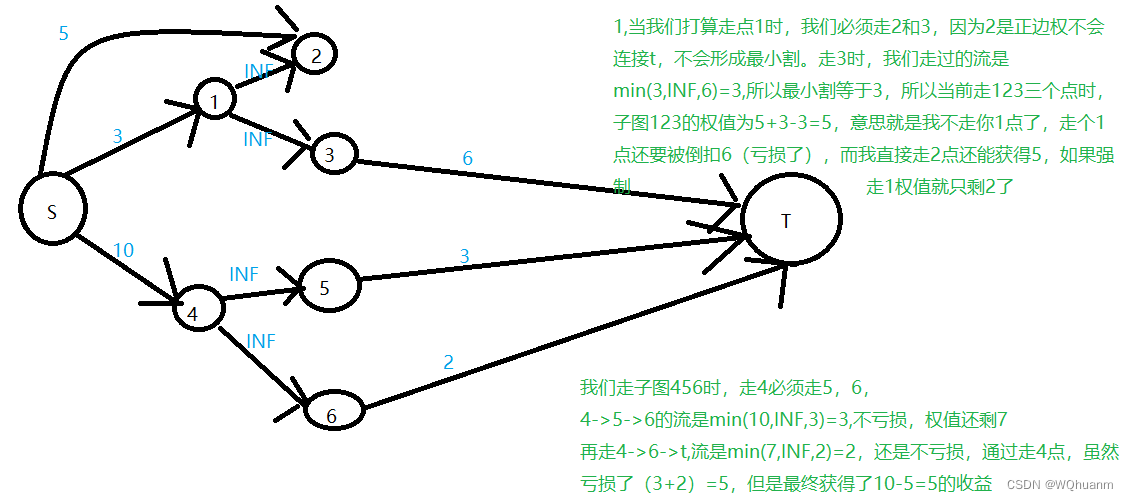
例题:Gold Mine
题意(读起来有点坑,翻译一下)
有t个测试,每个测试第一个输入n,表示有n个区域有金矿。
接下来对n个金矿进行描述,首先输入h,表示这个金矿有h个金块。
接下来对h个金块描述,首先是a1,a2,w表示挖这个金块的代价,挖这个金块获得的价值,挖这个金块前必须先挖掉前面w个金块才可以。
接下来对w个金块描述,每行输入x1,x2,表示这个金块在x1行,x2列。
思路:
就是裸题.......
我用的isap算法最大流三大算法——3,ISAP算法
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define int ll
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
typedef pair<int, int> pii;
//double 型memset最大127,最小128
//std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
const int INF = 0x3f3f3f3f; //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int M = 5e4 + 10;
const int N = 3e3 + 10;
int head[M], gap[N], dep[N], now[M];
int num, ans, s, t, cnt;
struct node
{
int next, to, w;
} edge[M];
void add(int u, int v, int w)
{
edge[++num].next = head[u];
edge[num].to = v;
edge[num].w = w;
head[u] = num;
edge[++num].next = head[v];
edge[num].to = u;
edge[num].w = 0;
head[v] = num;
}
void init()
{
memset(head, 0, sizeof(head));
memset(dep, -1, sizeof(head));
memset(gap, 0, sizeof(gap));
num = 1;
ans = cnt = 0;
}
void bfs()
{
queue<int>q;
dep[t] = 0;
gap[0]++;
q.push(t);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i; i = edge[i].next)
{
int v = edge[i].to, w = edge[i ^ 1].w;
if (dep[v] == -1 && w)
{
dep[v] = dep[u] + 1;
gap[dep[v]]++;
q.push(v);
}
}
}
}
ll dfs(int u, ll sum)
{
if (u == t)return sum;
int k, res = 0;
for (int i = now[u]; i && sum; i = edge[i].next)
{
now[u] = i;
int v = edge[i].to, w = edge[i].w;
if (dep[v] == dep[u] - 1 && w)
{
k = dfs(v, min(sum, w));
if (!k)continue;
edge[i].w -= k;
edge[i ^ 1].w += k;
res += k;
sum -= k;
if (!sum)return res;
}
}
gap[dep[u]]--;
if (!gap[dep[u]])dep[s] = cnt + 2;
dep[u]++;
gap[dep[u]]++;
return res;
}
void msolve()
{
init();
int n, h, a1, a2, w, sum = 0;
cin >> n;
s = 0, t = 25 * n + 1;
for (int i = 0; i < n; ++i)
{
cin >> h;
for (int j = 1; j <= h; ++j)
{
cnt++;
int u = i * 25 + j;
cin >> a1 >> a2 >> w;
int a = a2 - a1;
if (a > 0)add(s, u, a), sum += a;//正权值点连接s,负权值点连接t
else add(u, t, -a);
for (int k = 1; k <= w; ++k)
{
cin >> a1 >> a2;
add(u, (a1 - 1) * 25 + a2, llINF);//点与点之间边是INF
}
}
}
//isap算法
bfs();
while (dep[s] < cnt + 2 && dep[s] != -1)
{
memcpy(now, head, sizeof(head));
ans += dfs(s, llINF);
}
cout << sum - ans << endl;
}
int32_t main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
for (int i = 1; i <= t; ++i)
{
cout << "Case #" << i << ": ";
msolve();
}
return 0;
}