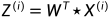Data Mining

一、概述

1.1 数据挖掘 VS 机器学习 VS 深度学习 VS 知识发现

知识发现：
知识发现就是在数据中发掘知识，将低层次的原始数据转换为高层次的信息。

数据挖掘：

数据挖掘是用一系列的方法或算法从数据中挖掘有用的信息，是知识发现中的核心工作。

机器学习：
机器学习是研究如何使用计算机来模拟或实现人类的学习行为的技术，是数据挖掘的重要方法。

深度学习：
使用人工神经网络可以根据数据集训练出基本规则，是当前使用机器学习研究AI的重要方法。

人工智能：

人工智能 (AI) 指用算法构建动态计算环境来模拟人类智能过程。

1.2 三大机器学习类型

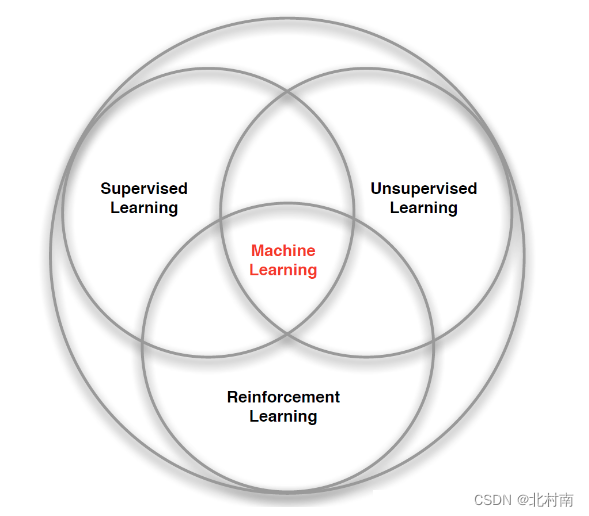
• 有监督学习

  有标签，包括分类、回归

• 无监督学习

  无标签，包括聚类分析、关联规则、特征降维度

• 强化学习

  标签，包括MDP马尔科夫决策过程，是研究智能体与环境交互中如何达到最大奖励

无监督学习 VS 强化学习

二者虽然都是无标签，但是学习的目的不同，无监督学习是从大量无标注数据集中发现隐藏结构，而强化学习的目标是最大化奖励，无监督的学习方法可以对强化学习有帮助，但无法解决根本问题

1.3 数据挖掘三大基本任务

• 聚类分析
• 关联规则
• 分类预测

二、分类器

2.1 混淆矩阵

T or F 都是相对于预测而言

• TP（True Positive）
• TN（True Negative）
• FP（False Positive）
• FN（False Negative）

2.2 性能指标

• 准确率(Accuracy)

  含义：所有样本中正确预测的情况

  $$Accuracy=\frac{TP+TF}{TP+FP+TN+FN}$$

• 精确率(Precision)

  含义：预测正样本中确实为正样本的情况

  $$Precision=\frac{TP}{TP+FP}$$

• 召回率(Recall)/灵敏度(Sensitivity)

  含义：实际正样本中正确预测正样本的情况

  $$Recall=Senstivity=\frac{TP}{TP+FN}$$

• 特异度(Specificity)

  含义：实际负样本中正确预测负样本的情况

  $$Specificity=\frac{TN}{TN+FP}$$

• F1-Score

  含义：兼顾分类模型的精准率和召回率，为二者的调和平均数

  $$F1-score=2\ast \frac{Precision\ast Recall}{Precision+Recall}$$

• ROC
  

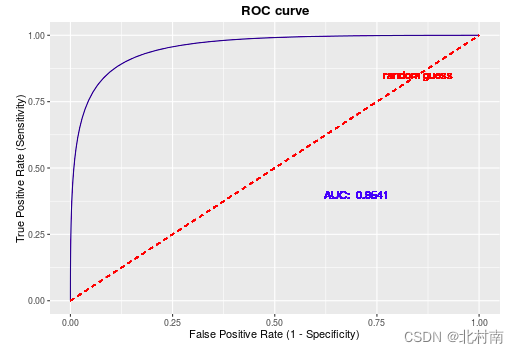
  横坐标：1-Specificity 特异度

  纵坐标：Sensitivity 灵敏度

• AUC

  • AUC(Area Under Curve),为ROC曲线下方的面积
  • 由于ROC曲线一般都是在y=x直线的上方，因此取值一般是在0.5~1.0之间
  • 区别：ROC只是条曲线，而AUC是具体的数值，从而更好的判断分类器的好坏
  • 若ROC曲线在y=x下方，最简单的方法就是将预测值取反

2.3 交叉验证

• 目的：一种更可靠的模型评估方法
• 具体方法
  1. 将数据集平均分成K份
  2. 使用1份数据作为测试集，其余作为训练数据
  3. 每个子样本都作为一次测试集
  4. 将k次测试结果取平均

2.4 KNN

• 含义：K-Nearest Neighbor，K最邻近算法，在已知标号类的数据集中，通过测量不同对象之间的距离（默认是欧式距离）进行分类，也可用以回归

• Euclidean距离（欧式距离）

  $$d(x,y)=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$

• Manhattan距离（曼哈顿距离）

  $$d(x,y)=\sum _{i=1}^n|x_i-y_i|$$

  例：两个点A(x1, y1)，B(x2, y2)

  $$d(A，B)=|x_1-x_2|+|y_1-y_2|$$

• Chebyshev距离（切比雪夫距离）

  $$d(x,y)=ma{x}_{i=1,2,3,...,n}^n|x_i-y_i|$$

  例：两个点A(x1, x2, x3)，B(y1, y2, y3)距离为

  $$d(x,y)=max(|x_1-y_1|,|x_2-y_2|,|x_3-y_3|)$$

• Minkowski距离（闵可夫斯基距离组）

  $$d(x,y)=\sqrt[p]{\sum _{i=1}^n|x_i-y_i{|}^p}$$

  p是一个可变参数

  • 当p=1时，曼哈顿距离
  • 当p=2时，欧式距离
  • 当p→∞时，切比雪夫距离

  由此可以看出，闵可夫斯基距离不是一种距离，是一组距离的定义

• Nearest Neighbor

  • 定义：已有一个带标签的数据集，随后一个新样本过来，将新样本与所有老样本进行距离计算，得到TopK的距离值，K个样本中种类最多的就是新样本的类别
  • 对于新样本，只需要确定距离度量法则、K值、分类决策规则即可对其进行分类

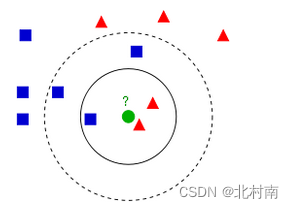
当K=3时，属于红色类。当K=5时，属于蓝色类

2.5 决策树

• 信息熵

  • 定义：可以理解为不确定度，一个系统的信息熵越大，其不确定性越大，越不纯净。
  • 公式：N代表样本的种类，pk代表某一类所占的比例。当pk=0时,H(X)=0

  $$H(X)=-\sum _{k=1}^N{p}_k{\log }_2\left(p_k\right)$$

  • 性质：样本分类越平均，信息熵越大，样本分类越聚集，信息熵越小
  • 熵：随机变量的不确定性

• 条件熵

  • 在一个条件下，随机变量的不确定性

  $$H(Y|X)=\sum _{x\in X}p(x)H(Y|X=x)$$

  • 例：H（Y|X=长相） = p(X =帅)H（Y|X=帅）+p(X =不帅)H（Y|X=不帅）

• 决策树

• 决策树包括叶节点和子节点

• 自顶而下分支，一条路径代表一条规则

• 如何生成决策树？

  • 选属性
  • 修剪决策树==如何选择根节点
    • 通过计算不同属性的不纯度方法，该方法包括信息增益Information Gain、信息增益比Gain Ratio、Gini-index、距离度量Distance Measure、J-measure
  • 例：从Age和Own_house中选出一个作为根节点
    

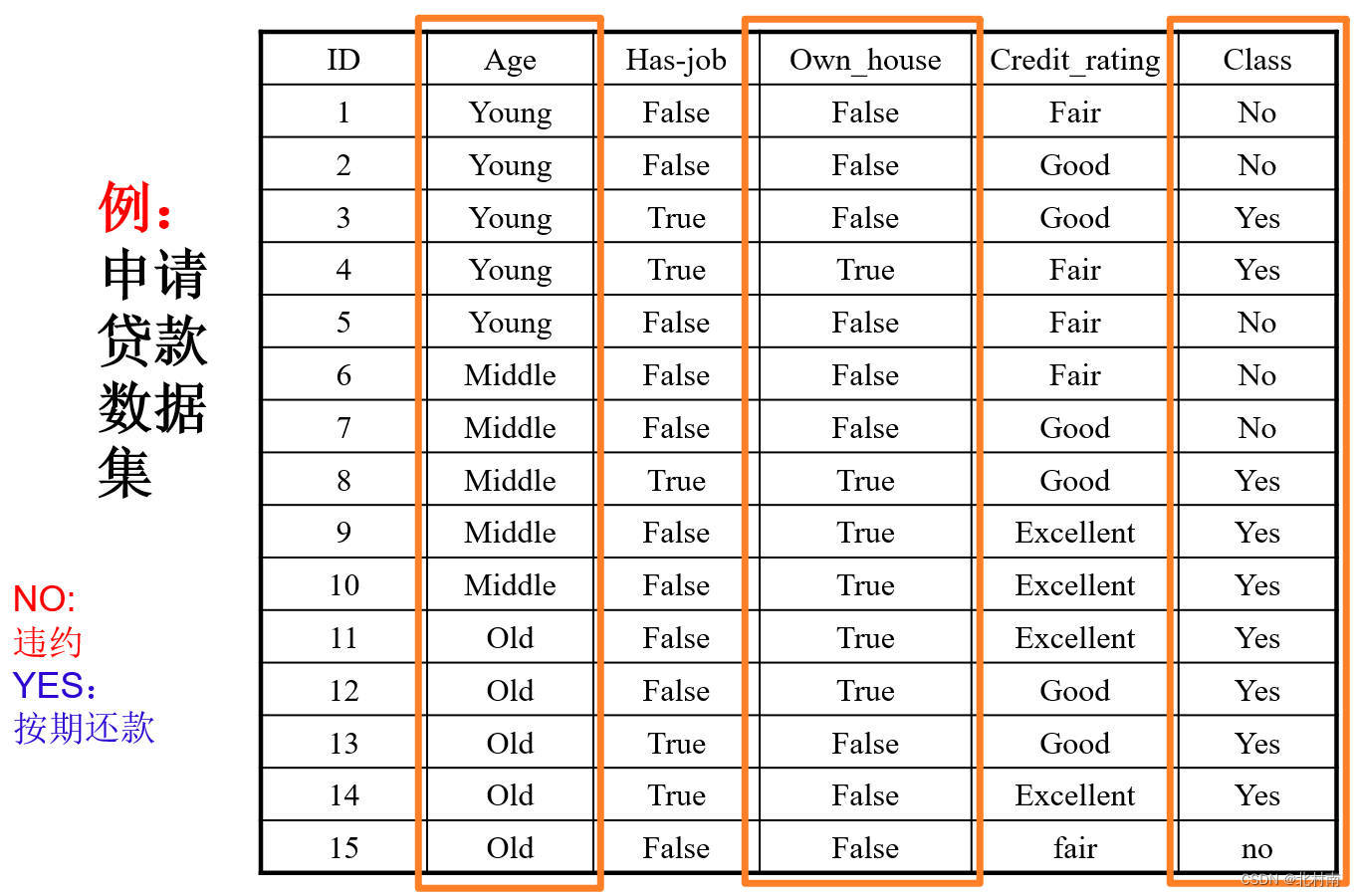
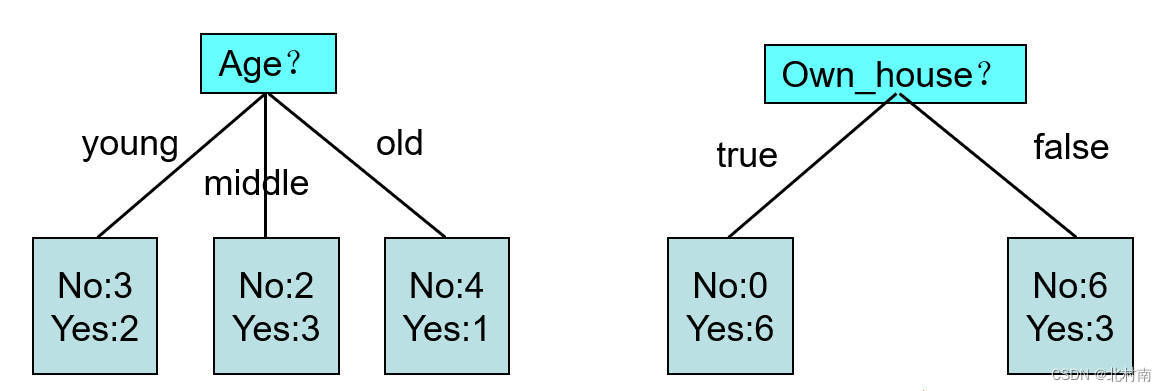
• Age的错误量是2+2+1=5（221是指每个年龄段错误量最少的），而Own的错误量是0+3=3。所以选择Own更合适

• ID3–信息增益

  • 定义：一个条件下，信息不确定性减少的程度（信息增益越大，则条件熵越小，信息不确定越小）简单的记法就是信息增加的多了，信息更加确定了

  $$信息增益=信息熵-条件熵$$

  • 例：判断嫁还是不嫁，用哪个作为根节点呢
    

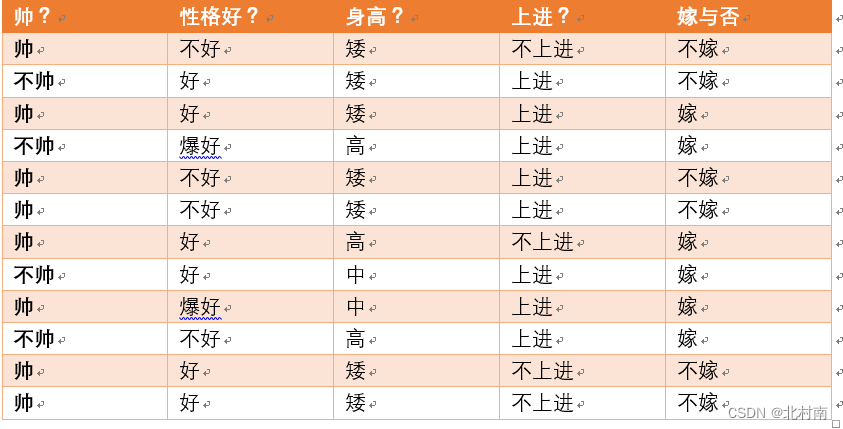
求解过程

1. 求得随机变量X（嫁与不嫁）的信息熵为：嫁的个数为6个，占1/2，那么信息熵为-1/2log1/2-1/2log1/2 = -log1/2=0.301

2. 现在假如我知道了一个男生的身高信息。

   身高有三个可能的取值{矮，中，高}

   矮包括{1,2,3,5,6,11,12}，嫁的个数为1个，不嫁的个数为6个

   中包括{8,9} ，嫁的个数为2个，不嫁的个数为0个

   高包括{4,7,10}，嫁的个数为3个，不嫁的个数为0个

3. 根据条件熵公式，我可以计算如下信息

   H(Y|X = 矮) = -1/7log1/7-6/7log6/7=0.178

   H(Y|X=中) = -1log1-0 = 0

   H(Y|X=高） = -1log1-0=0

   p(X = 矮) = 7/12,p(X =中) = 2/12,p(X=高) = 3/12

   条件熵=7/120.178+2/120+3/120 = 0.103*

4. 计算其他的信息量，如帅还是不帅的信息增益是0.112

5. 所以说条件身高的信息增量最大，信息的不确定减少最大，也就是说信息的确定性最好

6. 最终哪个大选哪个

• C4.5–信息增益比

  • 定义：在信息增益的基础之上，将分母统一化，即除以信息熵

  $$GainRadio(A)=\frac{Gain(A)}{SplitI(A)}$$

  CART-Gini指数

  • 定义：将信息熵的log部分换成Gini

  $$Gini(S)=1-\sum _{i=1}^C{p}_i^2$$

  $$\sum _{i=1}^{N}p(x_i)Gini(x_i)$$

  • 例：以身高为判断取值

  1. 取值划分为*{矮，不矮}*

  2. 矮包括{1,2,3,5,6,11,12}，嫁的个数为1个，不嫁的个数为6个

     不矮的有5个，嫁的个数为5个，不嫁的个数为0个

  3. Gini(X)=7/12(1-1/49-36/49)+5/12*(1-25/25-0/25)*

  4. 最终哪个小选哪个

• 联系

  1. ID3只能处理离散值，C4.5可以处理连续值
  2. ID3只能实现局部最优
  3. ID3对可能会导致过拟合
  4. C4.5使用了K折叠交叉验证
  5. C4.5可以处理缺省值

2.6 朴素贝叶斯

• 贝叶斯公式

  这里我们一般只会对比分子部分，分母部分不用算

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{P(B_1|A)P(B_2|A)...P(B_n|A)P(A)}{P(B)}$$

• 朴素是什么意思？

  在数据集中，特征之间互相独立

• 高斯朴素贝叶斯，高斯是什么意思？

  假设在条件下，所有特征都符合高斯分布（正态分布）

  $$P(x_i|y)=\frac{1}{\sqrt{2\pi {\sigma }_y^2}}{e}^{(-\frac{{({\sigma }_y-{\mu }_y)}^2}{2{\sigma }_y^2})}$$

  例：一个新的样本，其属性为收入低，是学生，信用良好，属于哪个类呢？
  

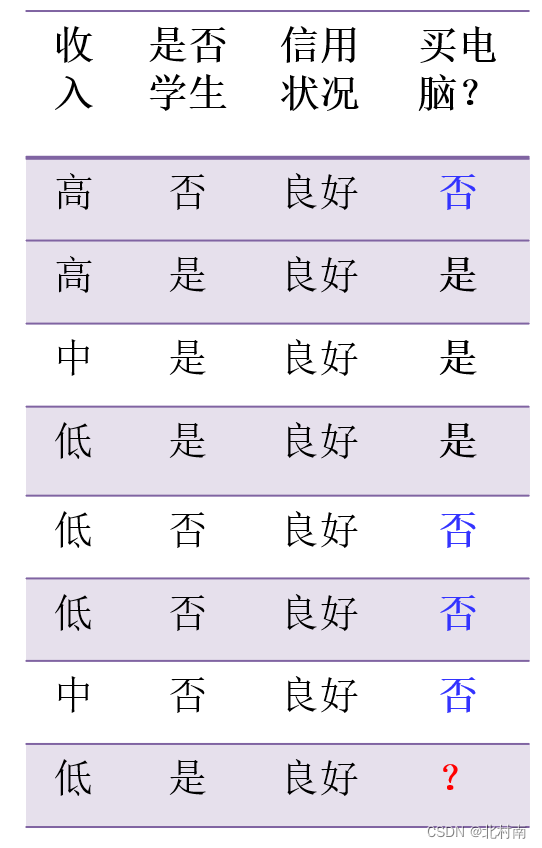
求解过程

1. 设X=(收入低，是学生，信用良好)
2. 根据朴素贝叶斯公式P(A|B)=~
3. *可知求解该问题的等价于比较P(X|买电脑)*P{买电脑}和P(X|不买电脑)P{不买电脑}
4. P(买电脑)=3/7 P(不买电脑)=4/7
5. 𝑃(𝑋|买电脑)=𝑃(收入低|买电脑) ∗𝑃(是学生|买电脑)∗𝑃(信用良好|买电脑) =(1/3)∗(3/3)∗(3/3)=1/3 𝑃(𝑋|不买电脑)= 𝑃(收入低|不买电脑)∗𝑃(是学生|不买电脑)∗𝑃(信用良好|不买电脑)=(2/4)∗(0/4)∗(4/4)=0
6. *P(X|买电脑)*P{买电脑} > P(X|不买电脑)P{不买电脑}
7. 因此预测会购买电脑

2.7 逻辑回归

• 定义：说白了就是Sigmoid函数和Softmax函数，将线性函数进行映射

$$f(x)=\frac{1}{1+e^{-x}}$$

$$S_i=\frac{e^{V_i}}{{\sum }_j{e}^{V_j}}$$

2.8 集成学习

• Bagging
  • 抽样：有放回
  • 定义：Bagging是一种根据均匀概率分布从数据集中重复抽样(有放回)的技术，子训练集的大小和原始数据集的大小是一样的，因此子训练集中的样本可能有重复。
  • 步骤：
    1. 原始数据集中样本共n个，每次有放回的抽取n个样本称之为自助数据集
    2. 重复上述过程，产生多个独立的自助数据集
    3. 每个自助数据集训练出一个基分类器
    4. 每个基分类器进行投票出最终判定结果
• Boosting
  • 抽样：无放回
  • 定义：Boosting是一种根据非均匀概率分布从数据集中抽取样本的技术，对于每一个样本，赋予不同的权重，当一条样本训练错误的时候会赋予更大的权重当做惩罚机制，将其视为困难样本，从而在下次训练时更多的关注它来更好的拟合函数
  • 步骤：
    1. 原始数据集中样本共n个，每个样本的初始权重都是1，训练第一代分类器
    2. 利用该分类器训练结果更新每个样本权重，难样本权重增加，易样本权重减小
    3. 训练下一代分类器
• Boosting和Bagging的区别
  • 放回+预测函数
  • Boosting：有放回的抽取样本，每个预测函数没有权重
  • Bagging：无放回的抽取样本，每个预测函数的权重是根据上一次训练误差决定的
• 随机森林
  • 基分类器采用的决策树算法：CART
  • 步骤
    1. 使用Bagging方法形成每颗树训练集
    2. 随机选取特征，使用Gini最小原则来选取属性
    3. 分类问题用投票，回归问题用平均
  • 随机森林是否是Bagging算法的一种特例？
    • 不能
    • 因为随机森林在特征选择上也是随机的，与Bagging算法不一样

三、回归

3.1 线性回归

• 一元线性回归

  • 简单线性回归模型

  $$y={\beta }_0+{\beta }_{1}x+ϵ$$

  • 换种写法是

  $$y=ax+b+ϵ$$

  • •a是斜率，b是截距，ε是偏差，它满足正态分布，所以其数学期望E(\epsilon)为0。所以由期望的性质，我们可以将上述公式写成

$$E(y)=b+ax$$

如何进行参数估计

$${\beta }_1=a=\frac{{\sum }_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{{\sum }_{i=1}n(x_i-\bar{x}{)}^2}$$

$${\beta }_0=b=\bar{y}-{\beta }_1\ast \bar{x}$$

• 多元线性回归模型

$$E(y)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+.......+{\beta }_n{x}_n$$

将其转化成矩阵形式

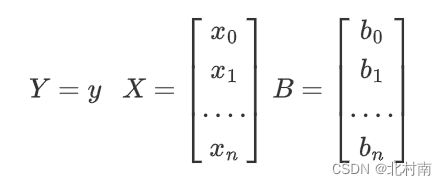
即为

$$Y=B^{T}X$$

进行函数拟合，找到矩阵B使得Loss尽可能的小

$$\begin{gathered} j(B)=\frac{1}{2n}\sum _{i=1}^n(h(x_i)-y_i{)}^2 \\ j(B)=\frac{1}{2n}(XB-y{)}^T(XB-Y) \end{gathered}$$

• 最小二乘法

  • 一元线性回归方程

  $$\begin{gathered} {\beta }_1=a=\frac{{\sum }_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{{\sum }_{i=1}n(x_i-\bar{x}{)}^2} \\ {\beta }_0=b=\bar{y}-{\beta }_1\ast \bar{x} \end{gathered}$$

  • 多元线性回归方程

忽略推导过程，最终回归系数求得为

$$B={\left(X^{T}X\right)}^{-1}{X}^{T}Y$$

• 梯度下降法

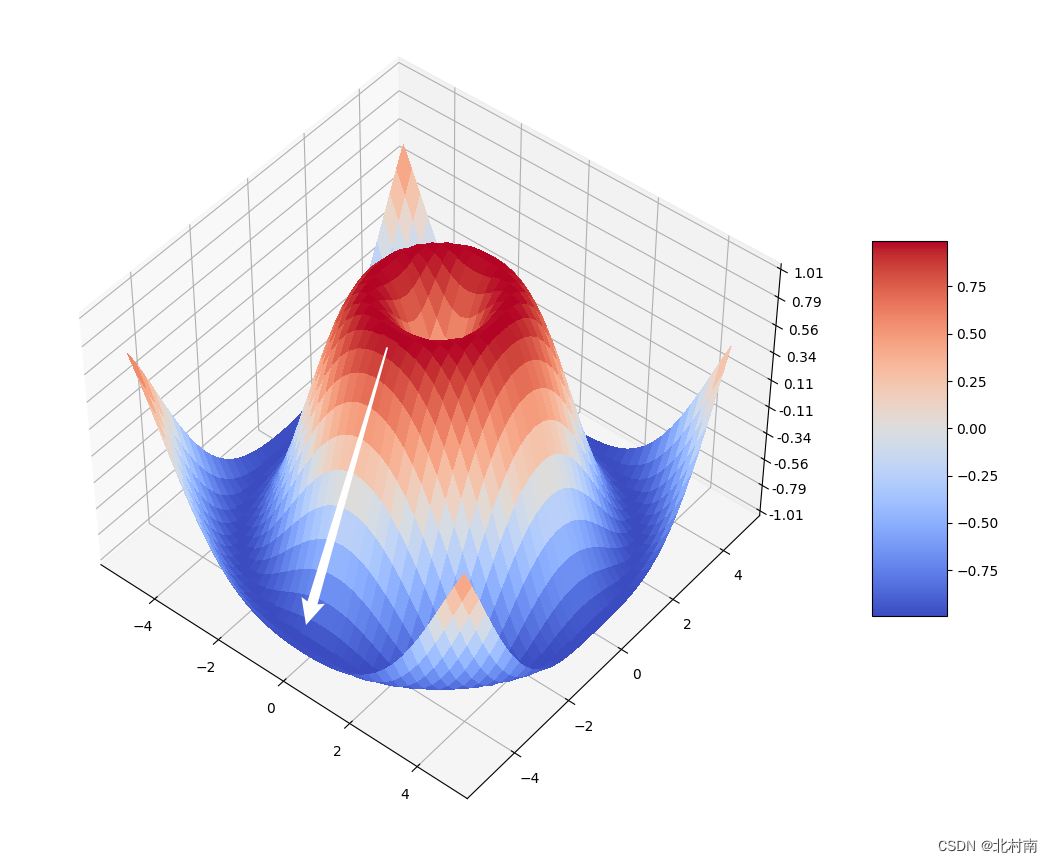
  • 定义：对函数不断的求梯度，就像人如何下山最快，每走一段距离调整好方向，走坡度最大的方向
    

3.2 损失函数

• 交叉熵损失函数

  • 场景：分类

  $$MSE=\frac{1}{n}\sum _{i=1}^n{(Y-Y_{pred})}^2$$

• 均方误差

  • 场景：回归

  $$CE=\frac{1}{n}\sum _{i=1}^n\left[Yln(Y_{pred})\right]$$

3.3 神经网络

• 激活函数
  

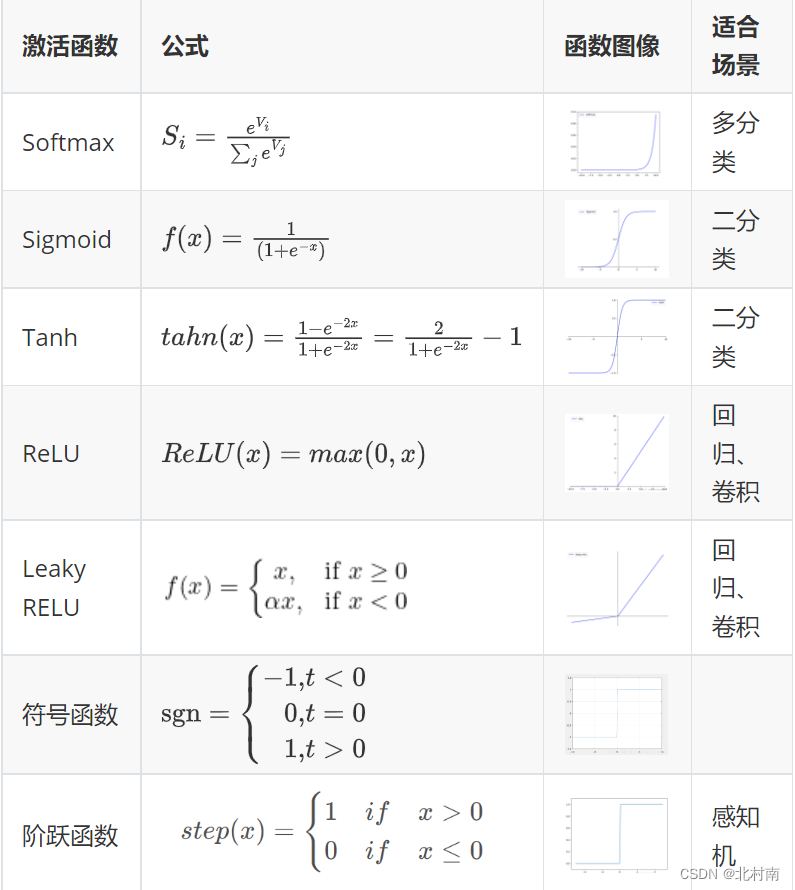
  • 特性
    • 可微，优化方法是基于梯度
    • 单调，保证单层网络是凸函数
    • 输出值范围，有限则使得梯度优化更稳定
    • 将感知机的激活函数从符号函数换成其他的，即进入神经网络的世界

• 感知机

  • 单层感知机

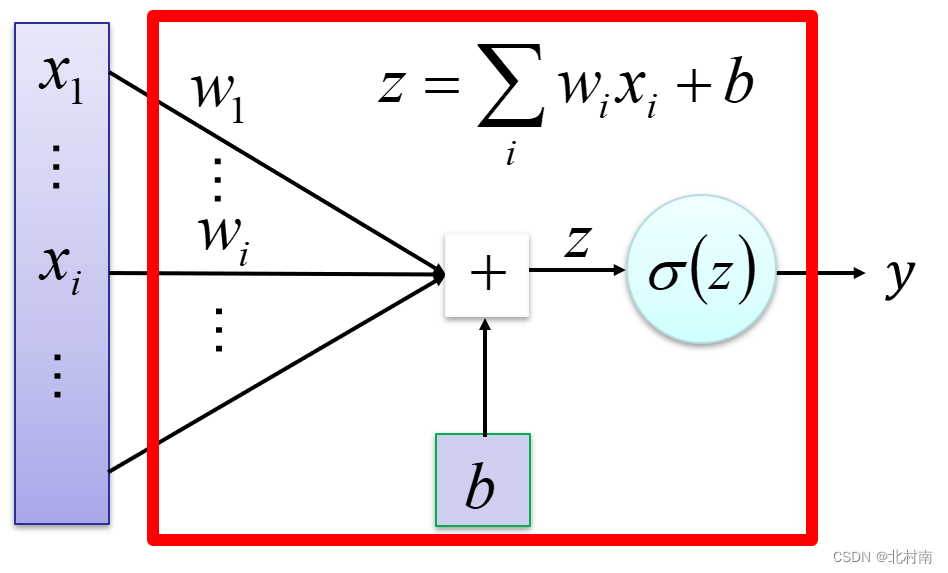
    • 定义：一个使用阶跃/符号函数作为激活函数的简单神经元，仅包含一个权值可调
      

  • 多层感知机

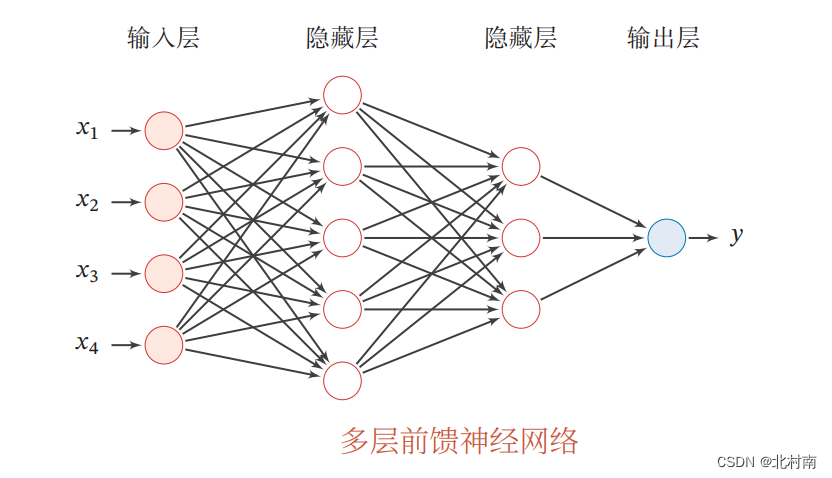
    • 定义：全连接神经网络
      

四、聚类分析

4.1 划分聚类

• K-means

• 算法步骤

  1. 首先得到一个初始的划分，产生K个初始簇
  2. 计算每个簇的中心
  3. 将每个对象重新归于最近的中心
  4. 重复2、3直到满足结束条件(划分没有变化、达到最大迭代次数、目标函数没有改进)

• 评价标准

  其中k是簇的个数，p是Ci中的样本，mi是簇mi的均值。说白就是计算所有点和该点所在簇的平均值的平方误差。

  当平方误差达到最小值时，簇内样本较紧密，簇间样本较分散

$$E=\sum _{i=1}^k\sum _{p\in C_i}|p-m_i{|}^2$$

4.2 层次聚类

• AGNews

• 算法步骤

  1. 将数据集中的每个样本作为一个簇
  2. 按照合并准则将簇逐步合并
  3. 直到不能合并或达到终止条件

  合并准则

  1. 每次周到距离最近的两个簇进行合并
  2. 两个簇之间的距离由这连个簇中距离最近的样本决定
     

4.3 密度聚类

• DBSCAN
  

• 核心点

  在该点半径内有超过MinPts数目的点

• 边界点

  在该点半径内没有超过MinPts数目的点，但是半径内有核心点

• 噪音点

  在该点半径内没有超过MinPts数目的点，且半径内无核心点

• 密度直接可达

  从核心点A出发，到半径内另外一个点B，则称A密度直接可达B

• 密度可达

  从核心点出发A，到半径内另外一个核心点B1，不断相连到B，则称A密度可到B

• 密度连通

  A密度可到B和C，则称B和C是密度相通

五、特征降维

5.1 PCA

• 目标：找到一个映射函数，将高维的原始特征空间映射到低维的特征空间中去

• 步骤

  1. 比如说将一个n个d维的特征降低到n个k维的特征
  2. 先将所有的特征组成d行n列的矩阵，记为X
  3. 计算X的协方差矩阵、特征值、特征空间
  4. 根据特征值大小来降序排列特征向量
  5. 选取TopK行特征向量组合成矩阵P
  6. Y=XTP就是最终结果

• 第一主成分

  将坐标轴中心移动到数据中心，旋转坐标轴，使得坐标轴在F1方向上的方差最大，即所有数据在该方向上最分散，也意味着在该方向上保留更多的信息。F1即为第一主成分

• 第二主成分

  找到多个F2方向，使得F2与F1的协方差为0，以免与F1的信息重叠，在众多F2方向中，和F1方向寻找的办法一样，某方向方差最大就是第二主成分

5.2 PCA VS AutoEncoder

• PCA
  • PCA是一种无监督技术，将原始数据投影到若干高方差方向（维度）
  • 这些高方差方向彼此正交，因此投影数据的相关性非常低或几乎接近于 0。这些特征转换是线性的。
• AutoEncoder
  • 自动编码器是一种无监督的人工神经网络，它将数据压缩到较低的维数，然后重新构造输入
  • 自动编码器通过消除重要特征上的噪声和冗余，找到数据在较低维度的表征
  • 它基于编解码结构，编码器将高维数据编码到低维，解码器接收低维数据并尝试重建原始高维数据
• 联系
  • PCA可以看成是一个含有一个隐层（线性激活函数）的神经网络。（即可看做是单层且使用线性激活函数的AutoEncoder）
• 区别
  • 变换上，PCA只能做线性变换，AutoEncoder既可以做线性变换也可以做非线性变换
  • 参数上，PCA只有正交向量的参数，而AutoEncoder是大量的神经网络参数

六、关联规则

6.1 支持度

• 定义：就是字面意思，支持的程度。假定某个数据集T中有N条数据，X表示数据集中的某个事务，那么支持度的计算公式如下

$$sup(X)=\frac{sum(X)}{N}$$

不难发现support(A)表示的就是A在该数据集中出现的频率

• 例：某超市某天有1000条订单，在这1000条订单里面，每一条订单都包含了许多商品。在这些订单里面有300个顾客购买的东西含有牛奶，那么对于牛奶来说，牛奶的支持度计算过程如下：

$$sup(牛奶)=\frac{sum(牛奶)}{N}=\frac{300}{1000}=0.3$$

在这1000个订单里面，有100个顾客既购买了牛奶，又购买了面包，那么事务{牛奶、面包}的支持度为：

$$sup(牛奶、面包)=\frac{sum(牛奶、面包)}{N}=\frac{100}{1000}=0.1$$

6.2 置信度

• 定义：表示在先决条件X发生的情况下，由关联规则”X→Y“推出Y的概率。

$$conf(X\to Y)=\frac{sup(X\cup Y)}{sup(X)}$$

• 例：引用上面使用过的例子，在超市的1000个订单中，购买了牛奶的有300个订单；既购买了牛奶，又购买了面包的订单有100个，那么我们可以很容易算出“牛奶→面包“的置信度，即客户购买牛奶后会购买面包的概率为：

$$conf(牛奶\to 面包)=\frac{sup(牛奶、面包)}{sup(牛奶)}=\frac{100}{300}=0.3333$$

• 意义：对于置信度的含义，我认为置信度揭示了X出现时，Y是否一定会出现，如果出现则其大概有多大的可能出现。如果置信度为100%,

  则说明了X出现时，Y一定出现。如果置信度太低，那么就会产生这样的疑问，X和Y关系并不大，也许与X关联的并不是Y。

6.3 频繁项集

• 定义：说白了就是经常（出现的频率超出某个指定的阈值）出现的集合。由于有阈值设定的原因，因此一个数据集中频繁项集可能不止一个

6.4 强关联规则

• 定义：关联规则是指事物之间的相互关联，若A和B之间有某个关系，那么我们可以通过预测A来预测B。

  强关联规则就是置信度和支持度均大于等于给定阈值

6.5 Apriori

• 目的：找出所有频繁项集，随后构造出满足用户的最小置信度规则
• 步骤
  1. 找出所有频繁i项集
  2. 通过频繁i项集找出所有频繁i+1项集，直到找到所有频繁项集
  3. 由频繁项集产生强关联规则
• 例：现有A、B、C、D、E五种商品的交易记录表，找出所有频繁项集，假设最小支持度>=50%,最小置信度>=50%
  

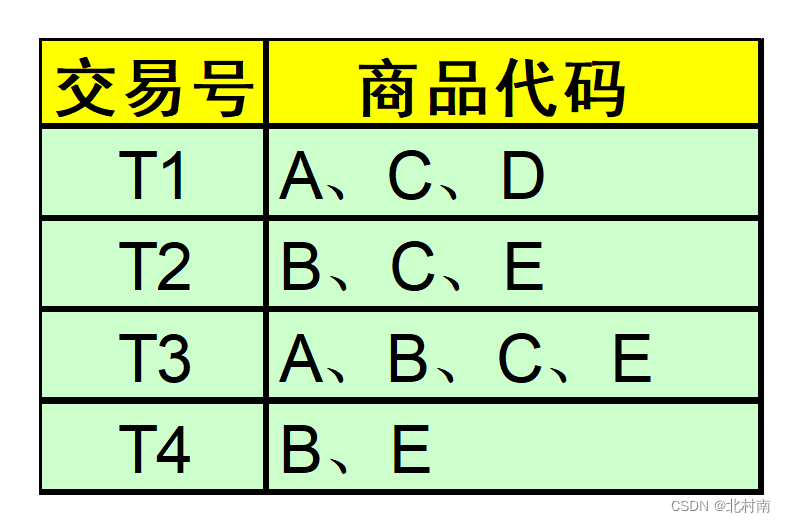
1. 计算L1支持度：Sup(A)=1/2 Sup(B)=3/4 Sup©=3/4 Sup(D)=1/4 Sup(E)=3/4
2. 删除不符合支持度的对象：删除{D}
3. 计算L2支持度：Sup(A,B)=1/4 Sup(A,C)=1/2 Sup(A,E)=1/4 Sup(B,C)=1/2 Sup(B,E)=3/4 Sup(C,E)=1/2
4. 删除 {A,B} {A,E}
5. 计算L3支持度：Sup(B,C,E)=1/2
6. 所以频繁项集共有9个，即 A B C E AC BC BE CE BCE
7. 最大频繁项集为 {BCE} {AC}
8. 计算L2以上的频繁项集的置信度，若其也大于阈值，则其为强关联规则

条件	结果
A→C C→A B→C C→B C→E E→B C→E E→C B→CE C→BE E→BC	~

6.6 推荐系统

• 基于用户的协同过滤UserCF
  

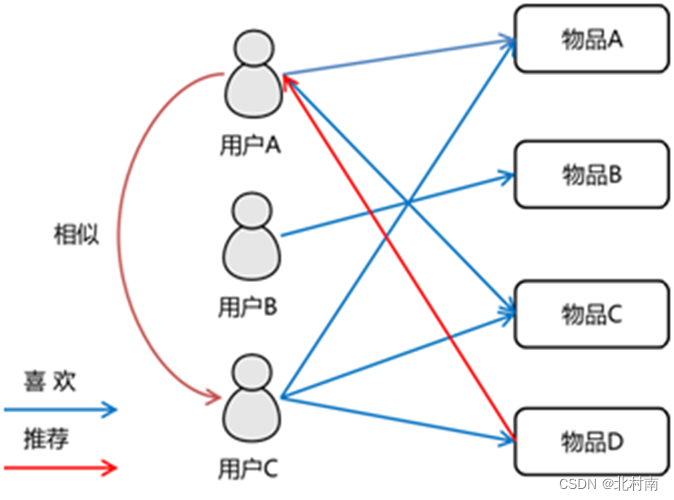
步骤

1. 计算用户之间的相似度
2. 根据相似度，找到这个群体的所有物品，将群体有的但是用户没有的物品进行推荐

相似度计算

令N(A)、N(B)分别表示A用户和B用户喜欢的集合

Jaccard公式

$$W_{AB}=\frac{|N(A)\cap N(B)|}{|N(A)\cup N(B)|}$$

余弦相似度公式

$$W_{AB}=\frac{|N(A)\cap N(B)|}{\sqrt{|N(A)|.|N(B)|}}$$

例：用两个公式计算u和v用户之间的相似度

1. Jaccard：Wuv=1/4
2. Cosine：Wuv=1/√6

最终推荐

如有A B C D 四个用户，推荐A用户物品，先计算与A最相似的K个（假如刚好是三个也就是B C D ），这K个中有哪些物品是A没有的，但是其他人有（如B和C有）

计算物品J的推荐度=WB+WC

• 基于物品的协同过滤ItemCF

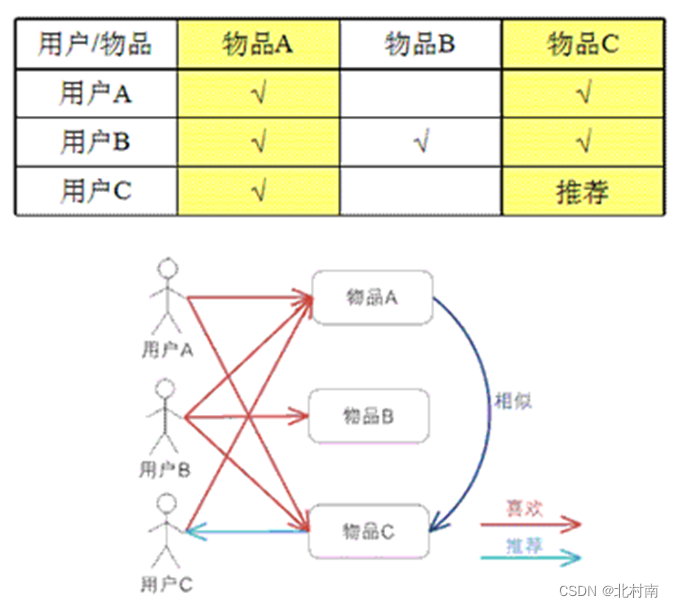
步骤

1. 计算物品之间的相似度
2. 推荐相似的物品给该用户

相似度计算

令N(A)、N(B)分别表示喜欢物品A和物品B的用户个数

$$W_{AB}=\frac{|N(A)\cap N(B)|}{\sqrt{|N(A)|.|N(B)|}}$$

最终推荐

已知用户u和它喜欢的物品j，R是对物品j的喜欢程度（如看过一次就设置为1），W是与物品j最形式的物品

$$p(u,j)=\sum _{i\in S(j,k)\cap N(u)}{W}_{ij}{R}_{iu}$$

• 基于模型的协同过滤

  方法：矩阵分解、关联规则算法、聚类算法、分类算法、回归算法、神经网络等

七、深度学习

7.1 什么是深度学习？

层数较多的多层感知机，一般层数至少超过3层

7.2 AI VS ML VS DL

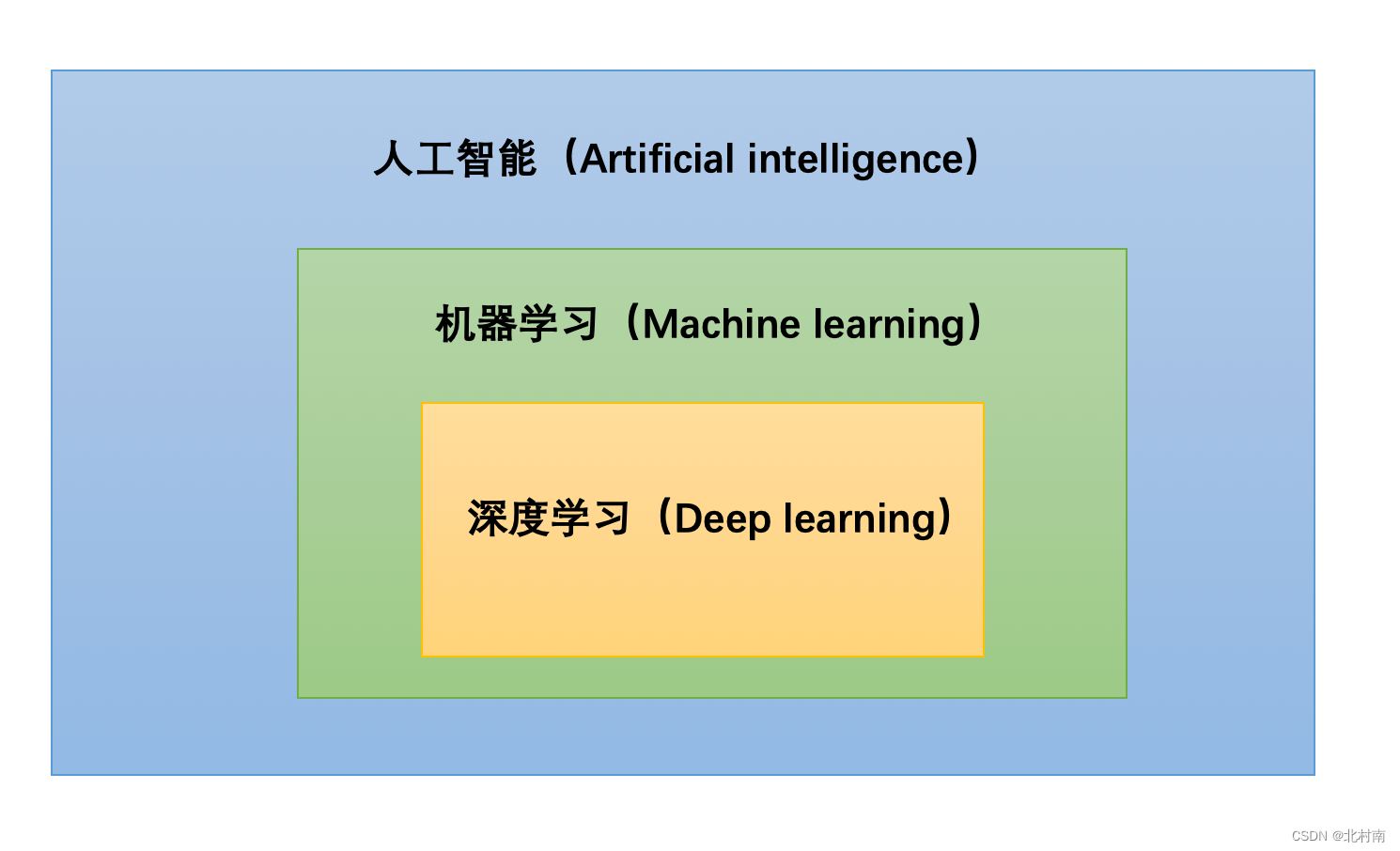
• 联系
  • ML是AI的一个子领域
  • DL是ML的一个子领域，ML中的神经网络构成了DL的深度学习的基础
• 区别
  • 区分DL和ML中神经网络的办法就是观察其网络节点层数，一般DL至少超过3层
  • ML需要复杂的特征工程进行特征提取，而DL特征可以自动生成
• 深度学习比传统机器学习的优点
  • 优异的性能：DL在各个领域的性能指标远超ML
  • 特征工程：DL不需要繁琐的特征工程
  • 适应性：DL适应性强，比如迁移学习可以使预训练网络迁移到其他同领域的不同应用上
  • 数据有效放缩：DL往往使用更多的数据，更容易扩展

7.3 FNN

• 定义：

• 参数量：

  $$D_{i-1}\ast D_i+D_i$$

7.4 CNN

• 卷积：不同数据窗口中的数据和卷积核做内积的操作

• 卷积核：一组固定权重的神经元，用来提取特定的特征

• 卷积层：多个卷积核叠加

• 池化：对一个数据窗口的数据按照某个规则(如最大值、最小值、平均值)取特定数据

• 参数量

  注意：参数量的大小和只和输入输出channel和Kernal有关，和Pooling、原图片大小都无关

  $$C_{in}\ast K\ast K\ast C_{out}+C_{out}$$

• 核心计算公式

  N：输出图片大小

  W：输入图片大小

  P：Padding大小

  K：Kernal大小

  S：Stride大小

  取整：卷积向下，池化向上

  $$N=\frac{W+2P-K}{S}+1$$

• 相比于FNN的优势

  CNN中使用了卷积权重贡献机制以及卷积操作，使得参数量大量的降低

7.5 RNN

• 定义：循环神经网络

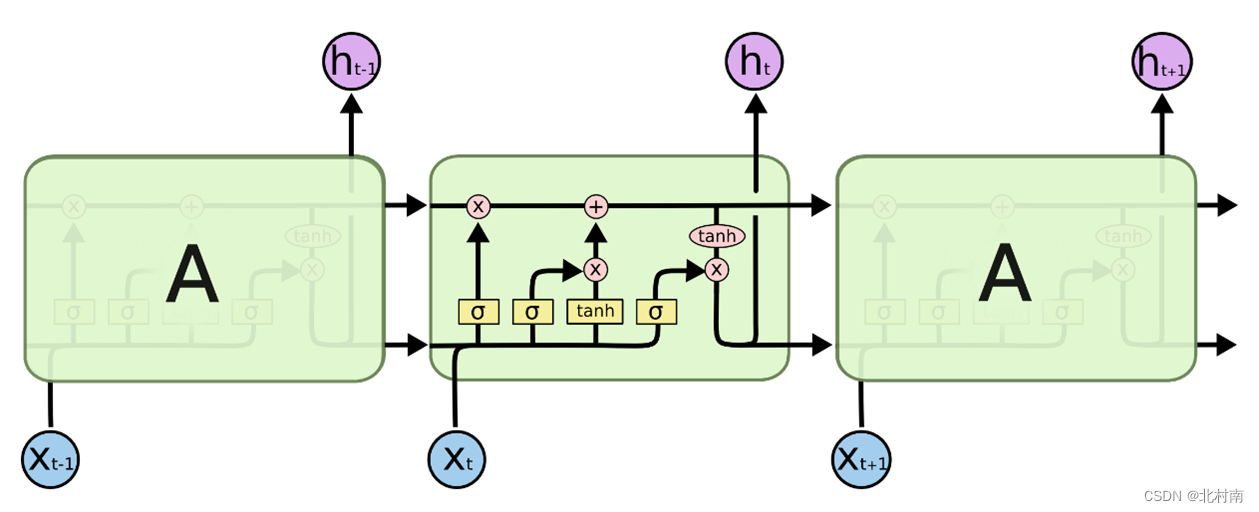
• GRU

  LSTM的简易版本，将遗忘门和输入门合并成一个更新门，所以一共有更新门→记忆门→输出门

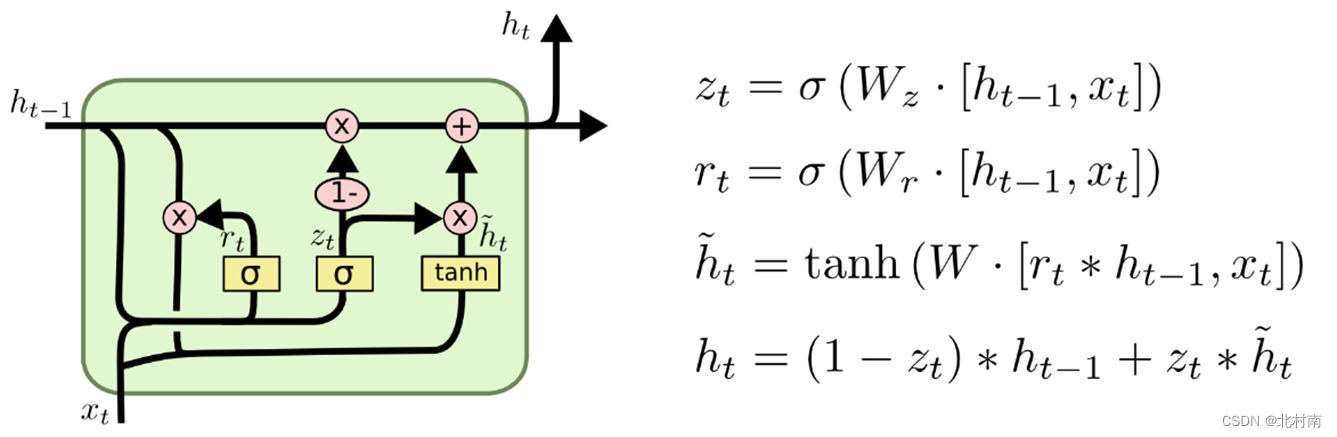
• LSTM

  一共有四个门：输入门→遗忘门→记忆门→输出门
  

7.6 Attention

• 定义：带注意力的网络，可以进行并行计算

• Self-Attention公式：

  $$Q=X{W}^{Q}Q\in R^{l\ast d}$$

  $$Att(Q,K,V)=Softmax(\frac{Q{K}^T}{\sqrt{D}})V$$

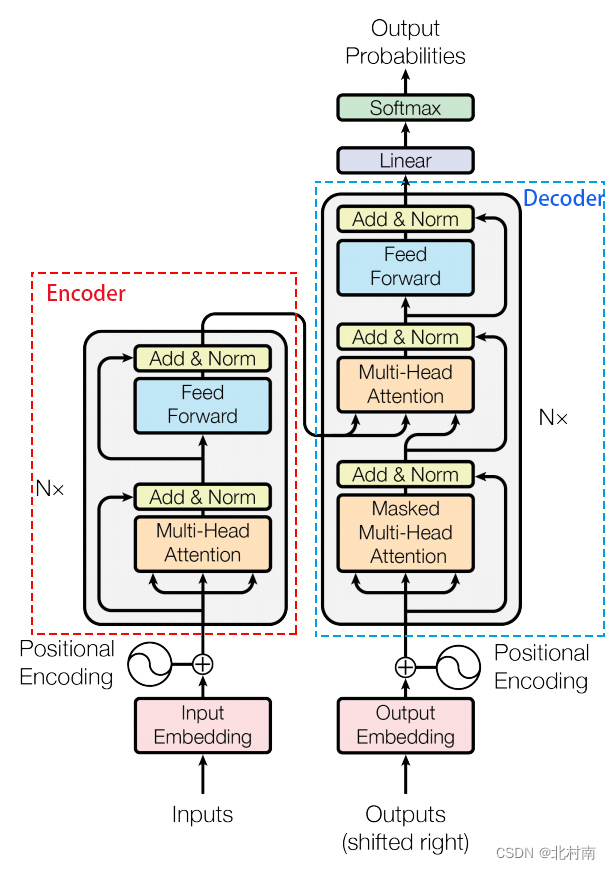
• Transformer

  • 多头注意力机制
  • 位置前馈网络
  • 层归一化
  • 残差连接
    

  层归一化公式

  $$y=\frac{x-E(x)}{\sqrt{Var(x)+ϵ}}\ast \gamma +\beta$$

最后祝大家考试都能取得好成绩！！！