摘要
1139. 最大的以 1 为边界的正方形
一、以1为边界的最大正方形
1.1 动态规划
第530题需要正方形所有网格中的数字都是1,只要搞懂动态规划的原理,代码就非常简洁。而这题只要正方形4条边的网格都是1即可,中间是什么数字不用管。
这题解题思路是这样的
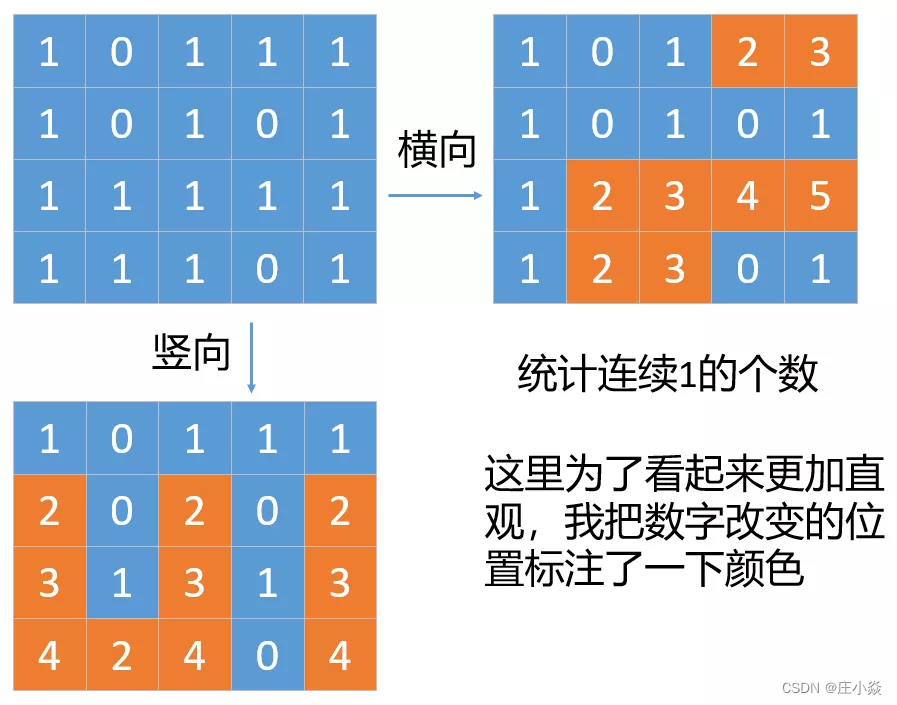
- 第一步先计算每个网格中横向和竖向连续1的个数。
- 第二步遍历二维网格,以每一个格子为正方形的右下角,分别找出上边和左边连续1的个数,取最小值作为正方形的边长,然后判断正方形的左边和上边长度是否都大于等于正方形边长,如果都大于等于正方形边长就更新正方形的最大边长,否则缩小正方形的边长,继续判断……。
代码比较简单,我们定义一个三维数组,其中
- dp[i][j][0]: (i,j)横向连续1的个数
- dp[i][j][1]: (i,j)竖向连续1的个数
第一步: 我们计算的时候,如果当前位置是0就跳过,只有是1的时候才计算,分别统计左边和上边(也就是横向和竖向)连续1的个数。代码比较简单,我们来看下(这里为了减少一些边界条件的判断,把dp的宽和高都增加了1)。
int m = grid.length;
int n = grid[0].length;
//dp[i][j][0]: (i,j)横向连续1的个数
//dp[i][j][1]: (i,j)竖向连续1的个数
int[][][] dp = new int[m + 1][n+1][2];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
//如果当前位置是0,就跳过
if (grid[i - 1][j - 1] == 0)
continue;
//如果是1,我们就计算横向和竖向连续1的个数
dp[i][j][0] = dp[i][j - 1][0] + 1;
dp[i][j][1] = dp[i - 1][j][1] + 1;
}
}第二步:找出正方形的最大边长
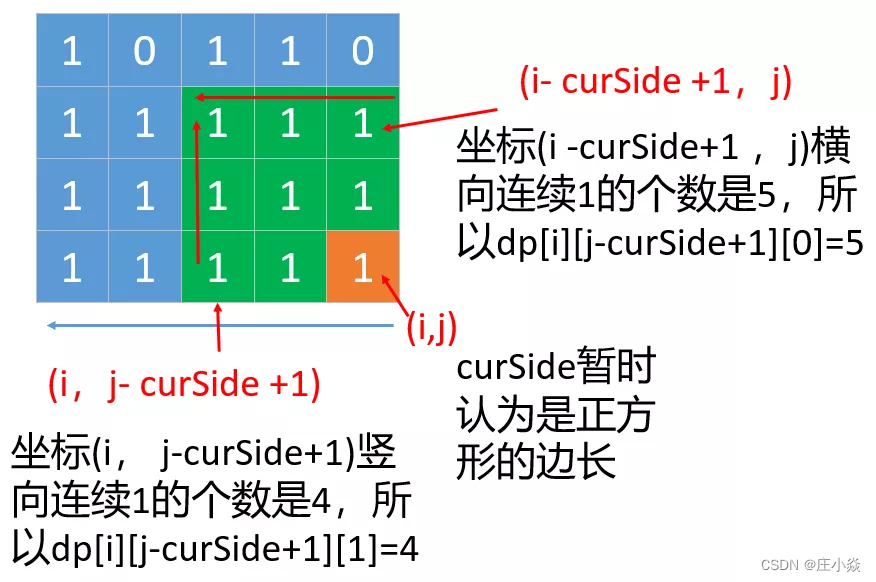
我们会以网格中的每一个位置为正方形的右下角,来找出正方形的边长。如下图所示,我们以橙色的位置1为正方形的右下角,分别沿着左边和上边找出他们连续1的个数,最小的作为正方形的边长。因为左边和上边连续1的个数我们在第一步的时候已经计算过,分别是dp[i][j][0]和dp[i][j][1],也就是正方形的边长我们暂时可以认为是
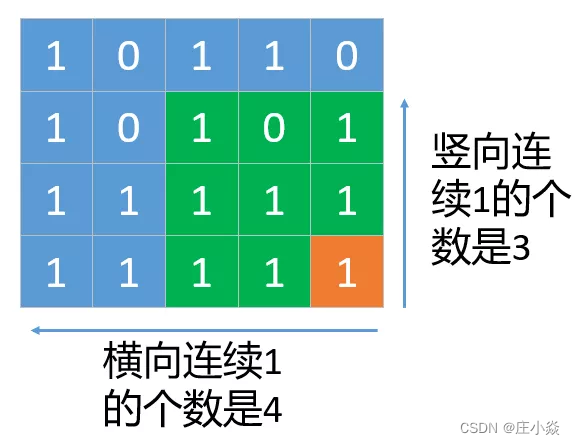
其实大家已经看到了这个边长就是正方形下边和右边的长度,但是正方形的上边和左边我们还没确定,我们继续确定正方形左边和上边的长度。会有两种情况
- 一种如下图所示,就是正方形左边和上边的长度都大于
curSide,我们可以认为以坐标(i,j)为右下角的正方形的最大长度就是curSide。
另一种如下图所示,正方形上边的长度是1,小于curSide。

这种情况下是构不成正方形的,所以我们要缩小curSide的值,然后再继续判断
public int largest1BorderedSquare(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
//dp[i][j][0]: (i,j)横向连续1的个数
//dp[i][j][1]: (i,j)竖向连续1的个数
int[][][] dp = new int[m + 1][n + 1][2];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
//如果当前位置是0,就跳过
if (grid[i - 1][j - 1] == 0)
continue;
//如果是1,我们就计算横向和竖向连续1的个数
dp[i][j][0] = dp[i][j - 1][0] + 1;
dp[i][j][1] = dp[i - 1][j][1] + 1;
}
}
int maxSide = 0;//记录正方形的最大长度
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
//沿着当前坐标往上和往左找出最短的距离,暂时看做是正方形的边长(正方形的具体边长
//还要看上边和左边的长度,所以这里要判断一下)
int curSide = Math.min(dp[i][j][0], dp[i][j][1]);
//如果边长小于maxSide,即使找到了也不可能再比maxSide大,所以我们没必要再找,直接跳过,
if (curSide <= maxSide)
continue;
//curSide可以认为是正方形下边和右边的长度,我们还需要根据正方形上边和左边的长度
//来确认是否满足正方形的条件
for (; curSide > maxSide; curSide--) {
//判断正方形的左边和上边的长度是否大于curSide,如果不大于,我们就缩小正方形
//的长度curSide,然后继续判断
if (dp[i][j - curSide + 1][1] >= curSide && dp[i - curSide + 1][j][0] >= curSide) {
maxSide = curSide;
//更短的就没必要考虑了,这里直接中断
break;
}
}
}
}
//返回正方形的边长
return maxSide * maxSide;
}复杂度分析
- 时间复杂度:O(m×n×min(m,n)),其中 m 表示矩阵的行数,n 表示矩阵的列数。
- 空间复杂度:O(m×n),其中 m 表示矩阵的行数,n 表示矩阵的列数。需要保存矩阵中每个位置的最长连续1的数目,需要的空间为 O(m×n)。
二、只是包含1的最大正方形
221. 最大正方形
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
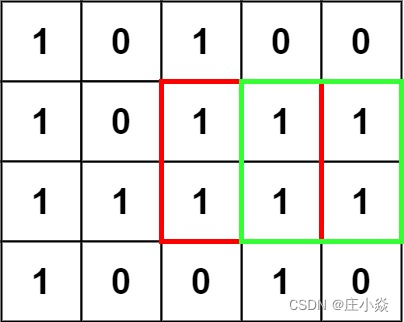
2.1 暴力求解
由于正方形的面积等于边长的平方,因此要找到最大正方形的面积,首先需要找到最大正方形的边长,然后计算最大边长的平方即可。
暴力法是最简单直观的做法,具体做法如下:
- 遍历矩阵中的每个元素,每次遇到 1,则将该元素作为正方形的左上角;
- 确定正方形的左上角后,根据左上角所在的行和列计算可能的最大正方形的边长(正方形的范围不能超出矩阵的行数和列数),在该边长范围内寻找只包含 1 的最大正方形;
- 每次在下方新增一行以及在右方新增一列,判断新增的行和列是否满足所有元素都是 1。

package matrix;
/**
* @Classname 最大的正方形221
* @Description TODO
* @Date 2023/2/17 7:50
* @Created by xjl
*/
public class 最大的正方形221 {
public int maximalSquare(char[][] matrix) {
int maxSide=0;
if (matrix==null||matrix.length==0||matrix[0].length==0){
return maxSide;
}
int rows=matrix.length,colums=matrix[0].length;
for (int i=0;i<rows;i++){
for (int j=0;j<colums;j++){
if (matrix[i][j]=='1'){
// 遇到一个 1 作为正方形的左上角
maxSide=Math.max(maxSide,1);
// 计算可能的最大正方形边长 剩下的矩阵中的最大的正方形
int currentMaxSide=Math.min(rows-i,colums-j);
for (int k = 1; k < currentMaxSide; k++) {
// 判断新增的一行一列是否均为 1
boolean flag = true;
// 判断是下一行和下一列是否为0 判断所有的对角线的元素 如果有存在的那就判断其他的四条边
if (matrix[i + k][j + k] == '0') {
break;
}
for (int m = 0; m < k; m++) {
if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {
flag = false;
break;
}
}
if (flag) {
maxSide = Math.max(maxSide, k + 1);
} else {
break;
}
}
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
}
2.2 动态规划求解
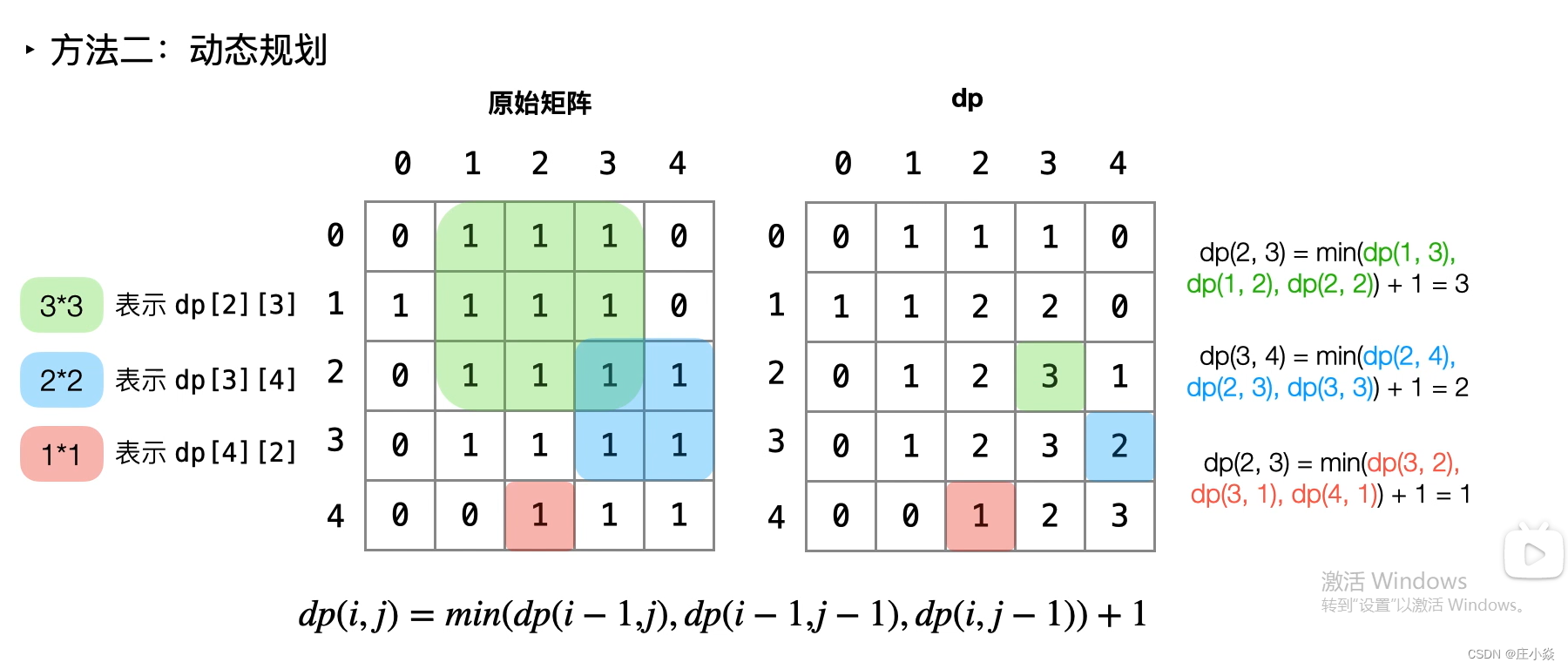
可以使用动态规划降低时间复杂度。我们用 dp(i,j) 表示以 (i,j) 为右下角,且只包含1的正方形的边长最大值。如果我们能计算出所有dp(i,j) 的值,那么其中的最大值即为矩阵中只包含1的正方形的边长最大值,其平方即为最大正方形的面积。
那么如何计算 dpdp 中的每个元素值呢?对于每个位置 (i,j)(i,j),检查在矩阵中该位置的值:
- 如果该位置的值是 0,则 dp(i,j)=0,因为当前位置不可能在由 1 组成的正方形中;
- 如果该位置的值是 1,则 dp(i,j)的值由其上方、左方和左上方的三个相邻位置的dp值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加1,状态转移方程如下:
此外,还需要考虑边界条件。如果 i 和 j 中至少有一个为0,则以位置 (i,j)为右下角的最大正方形的边长只能是 1,因此 dp(i,j)=1。
class Solution {
public int maximalSquare(char[][] matrix) {
int maxSide = 0;
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return maxSide;
}
int rows = matrix.length, columns = matrix[0].length;
int[][] dp = new int[rows][columns];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
maxSide = Math.max(maxSide, dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
}复杂度分析
- 时间复杂度:O(mn),其m 和 n是矩阵的行数和列数。需要遍历原始矩阵中的每个元素计算dp的值。
- 空间复杂度:O(mn),其中 m和n是矩阵的行数和列数。创建了一个和原始矩阵大小相同的矩阵 dp。由于状态转移方程中的 dp(i,j)由其上方、左方和左上方的三个相邻位置的 dp值决定,因此可以使用两个一维数组进行状态转移,空间复杂度优化至O(n)。
博文参考
《leetcode》