文章目录
- 1、统计量的定义
- 2、常用的统计量
- 3、经验分布函数
- 4、正态总体常用统计量的分布
- 4.1、卡方分布
- 4.1.1、卡方分布的定义
- 4.1.2、卡方分布的性质
- 4.2、t分布
- 4.2.1、t分布的定义
- 4.2.2、t分布的性质
- 4.3、F分布
- 4.3.1、F分布的定义
- 4.3.2、F分布的性质
- 5、正态总体的样本均值与样本方差的分布
- 5.1、定理一
- 5.2、定理二
- 5.3、定理三
- 5.4、定理四
样本是进行统计推断的依据,在应用时,往往不是直接使用样本本身,而是针对不同的问题构造样本的适当函数,利用这些样本进行统计推断。
抽样分布介绍的几个统计量的分布以及四个定理,都是在假定总体为正态这一情况下得到的。
1、统计量的定义

2、常用的统计量


3、经验分布函数


4、正态总体常用统计量的分布
统计量的分布称为抽样分布,在使用统计量进行统计推断时常需要知道它的分布。当总日的分布函数已知时,抽样分布是确定的,然而要求出统计量的精确分布,一般来说是困难的。下面介绍来自正态总体的几个常用统计量的分布
4.1、卡方分布
4.1.1、卡方分布的定义

4.1.2、卡方分布的性质

4.2、t分布
4.2.1、t分布的定义
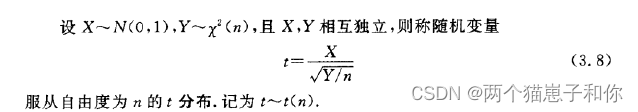
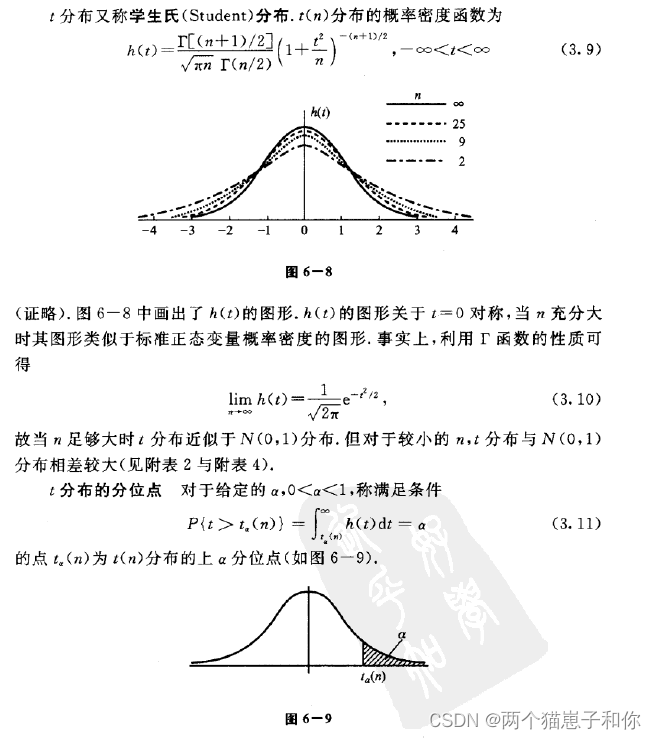
4.2.2、t分布的性质

4.3、F分布
4.3.1、F分布的定义
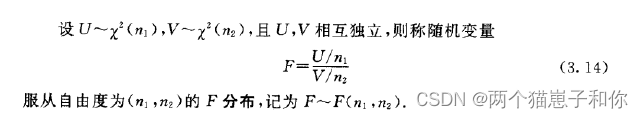
4.3.2、F分布的性质
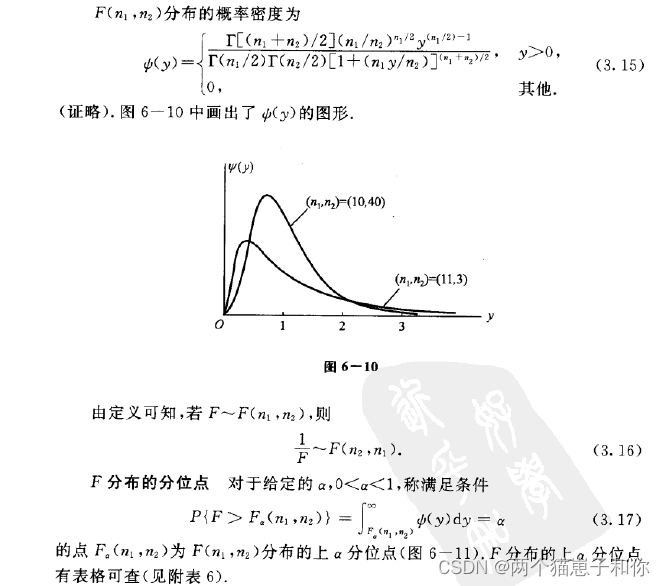
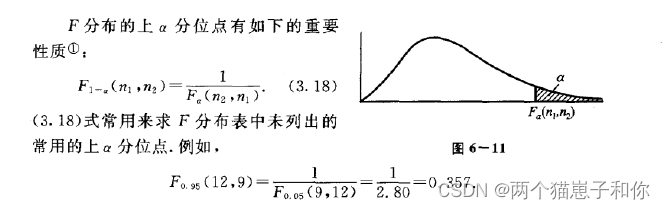
5、正态总体的样本均值与样本方差的分布

5.1、定理一
样本均值服从正态分布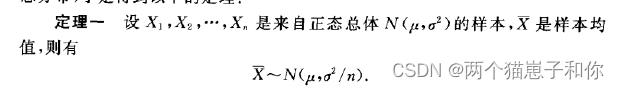
5.2、定理二
样本方差服从卡方分布

定理二的证明:


5.3、定理三
(样本均值-总体均值)/(样本标准差/根号下样本容量)服从自由度为n-1的t分布。

5.4、定理四