一、什么是Katalon
Katalon Studio 是一款免费的自动化测试工具,可以安装在windows、macOS、linux操作系统上,基于selenium 和 Appium 测试框架,并集成了这些框架的优点。工具使用简单方便,对于编码经验少,能力弱的测试人员也可以很快上手。
二、katalon的下载与安装
2.1、下载
Katalon 官网下载地址:https://www.katalon.com/download/(需要注册账号)。
2.2、安装
下载完毕,解压安装包,双击katalon.exe,打开katalon。
第一次安装,需要输入注册信息,注册成功之后,就可以使用了。
三、Katalon的界面介绍
Katalon Studio 的操作界面分布清晰,操作简单,新手使用时很容易上手。
3.1、整体界面介绍
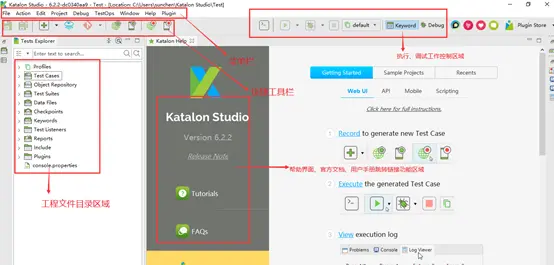
3.2、工具栏操作按钮介绍
主工具栏包含我们通常执行的最常见的操作。
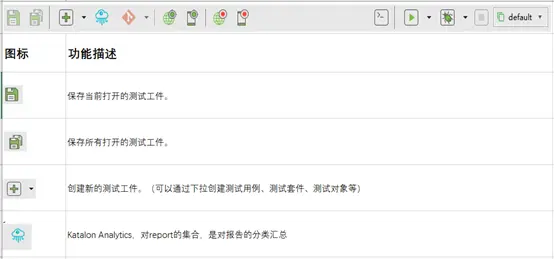


3.3、Tests Explorer
ests Explorer视图,也就是项目初始化后展示的主要界面;允许您浏览项目的结构并快速访问所有测试工件。使用视图上的上下文菜单,您可以创建新的工件,组织视图的项目,或者在需要时将它们拖放到特定的编辑器视图中。

3.4、目录文件简述
Profiles 配置文件–>当前项目的所有配置文件;
Test Cases 测试用例->当前项目中的所有测试用例;
Object Repository 界面元素->当前项目的所有测试对象;
Test Suites 测试套件->当前项目的所有测试套件和测试套件集合;
Data Files 测试数据文件->当前项目的所有测试数据;
Checkpoints 测试检查点->当前项目的所有测试用例的检查点;
Keywords 关键字函数->当前项目所有编写的关键字;
Test Listeners 测试监听->当前项目的所有测试监听;
Reports 测试报告->当前项目的所有生成报告;
Include 其他配置项;
Plugins 插件。
3.5、关键字工具集
关键字工具集,该试图显示了Katalon Studio预封装的所有可用关键字。在编写脚本时,您可以将关键字拖放到测试用例编辑器中。

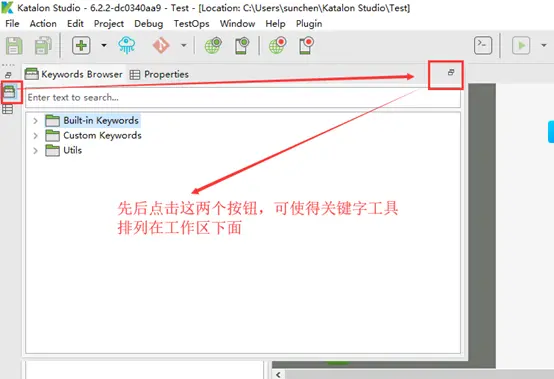
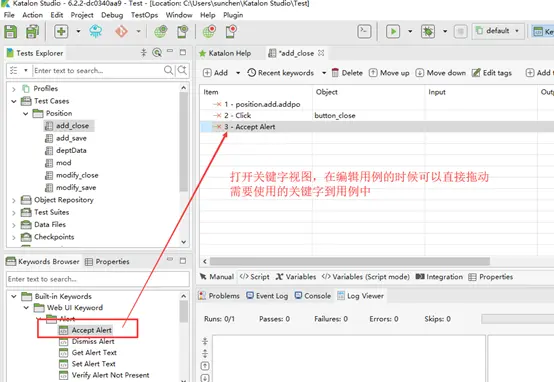
四、测试用例编辑器介绍
当我们新建一个用例或者打开一个测试用例时,它的详细信息会显示在包含以下选项卡的编辑器中:
Manual tab 通用编辑视图
Script tab 脚本编辑视图
Variables tab 变量编辑视图
Integration tab 集成工具编辑视图
Properties tab 属性选项视图
4.1、Manual tab 通用编辑视图
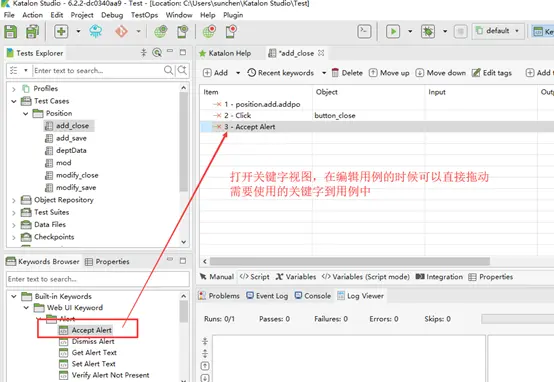
Manual tab为通用编辑模式,该编辑视图下可以通过操作方法名称检索并且选择需要使用的操作方法,也可以结合左树列关键字视图直接拖动需要使用的关键字到测试用例中。
(1) 通过索引选择关键字;
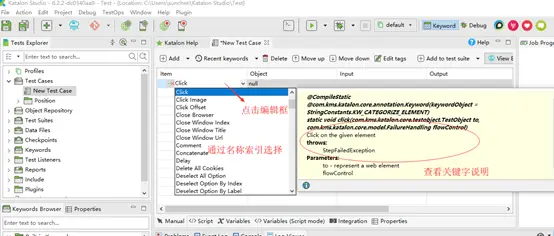
(2) 通过关键字视图选择关键字。
4.2、Script tab模式
Script tab编辑模式显示了对应的脚本视图,其中有编程基础的操作用户可以使用Groovy或Java语言轻松直接新增、修改、删除测试脚本。保存以后直接生成对应操作步骤的测试案例。
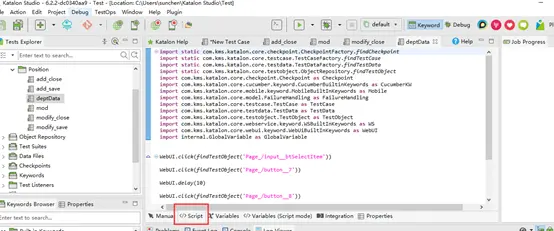
4.3、Variables tab模式
Variables tab模式显示为测试用例定义的所有公共变量,可以通过该界面定义所有变量的默认参数;在该界面新增的变量赋值以后,在执行该案例的时候读取的变量的数据为该部分所输入的数据。
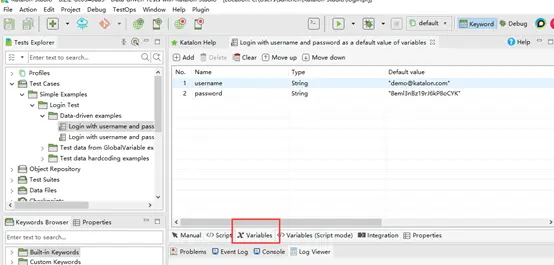
4.4、Integration tab模式
Integration tab模式,该编辑视图显示为测试用例与qTest和JIPRA的集成的信息显示在这个视图中。
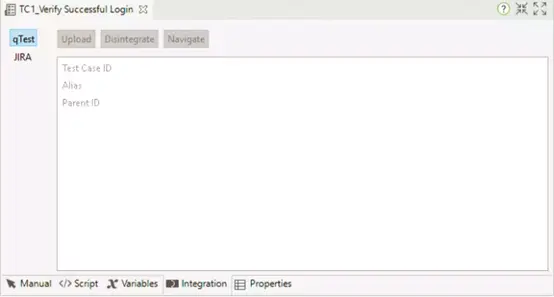
4.5、Properties tab模式
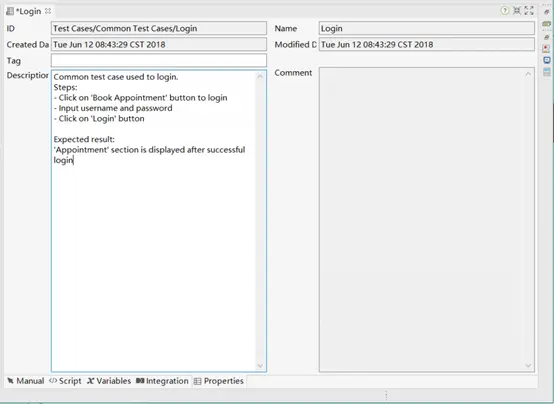
Properties tab模式,在该选项卡中显示关于测试用例的一般信息。
描述:用户可以添加或编辑该字段,以提供关于测试用例的详细信息。
注释:这个字段是只读的。内容从测试用例中的Comment关键字中提取并填充。业务用户可以通过提供需求来利用评论字段来参与开发过程。下面的例子展示了一个测试用例执行步骤的描述,以及输出执行结果。
五、katalon的初次使用
5.1、创建一个测试用例
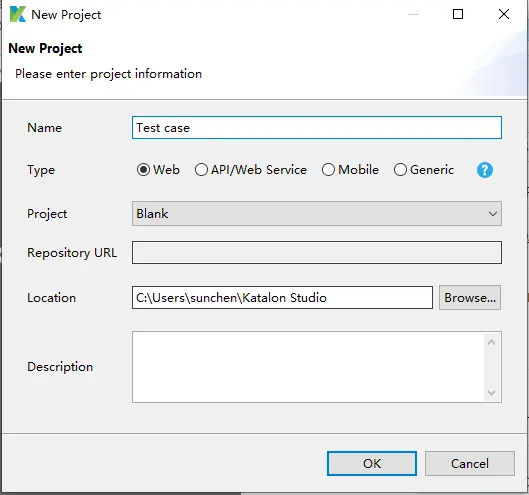
5.2、创建脚本
创建脚本分组:右击Test Cases——New——Floder;
右击Test——New——Test Case;
5.3、录制脚本
点击Record web;
输入访问地址与选择打开的浏览器,开始进行脚本的录制,直至脚本录制结束,点击下图红框处停止按钮并点击OK;
点击OK;
由于页面加载不确定性的存在,如网络延迟,需要手动配置操作的执行时间或顺序。可以在下图所示两个位置处进行修改:
a.在Manual tab视图中修改;
b.在Script tab视图中修改。
5.4、执行脚本
执行脚本,选择执行浏览器;
5.5、查看执行结果
5.6、创建用例的其他方法
除了以上这个录制脚本的方法,我们还有其他方法可以创建用例。
方法一:Spy web
用Spy Web功能添加对象到对象仓库中,在编写用例时,引用添加的对象。
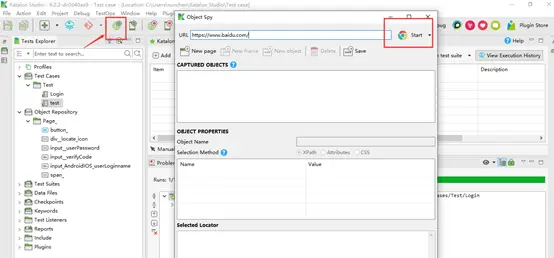


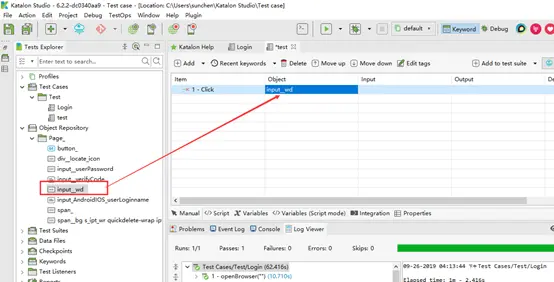
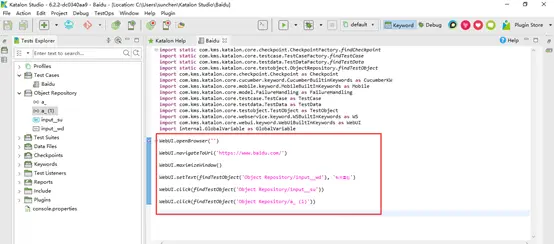
方法二:编辑脚本
如果你有比较好的代码能力,可以直接编辑脚本来写测试用例。
最后:下方这份完整的软件测试视频学习教程已经整理上传完成,朋友们如果需要可以自行免费领取 【保证100%免费】