题目描述

题目链接：867. 转置矩阵

给你一个二维整数数组 matrix， 返回 matrix 的 转置矩阵 。

矩阵的 转置 是指将矩阵的主对角线翻转，交换矩阵的行索引与列索引。

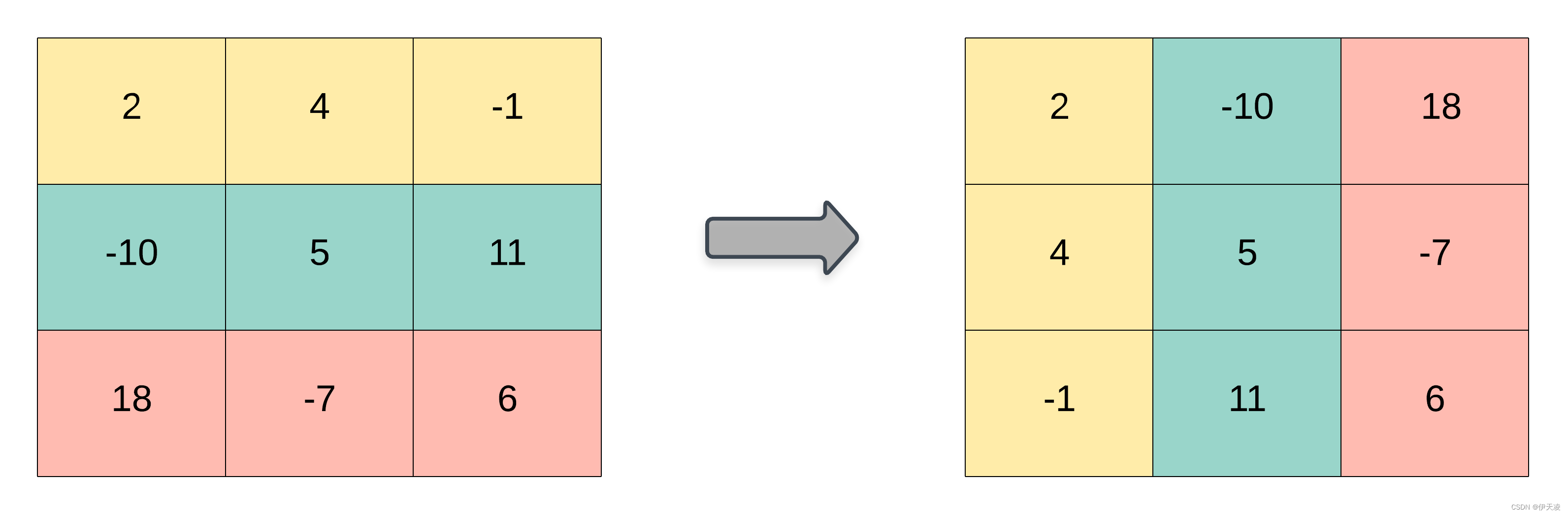
示例 1
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[1,4,7],[2,5,8],[3,6,9]]

示例 2
输入：matrix = [[1,2,3],[4,5,6]]
输出：[[1,4],[2,5],[3,6]]

提示

• m==matrix.length
• n==matrix[i].length
• 1 <=m, n<= 1000
• 1 <=m * n<= 10⁵
• -10⁹ <=matrix[i][j]<= 10⁹

---

解题核心

因为题目里面没有讲一定是方阵，所有原地修改应该是做不到的，需要新建一个转置长度的数组

解法一：二维表示 + 模拟

直接暴力遍历赋值

public int[][] transpose1(int[][] matrix) {
    int row = matrix.length;//行数
    int col = matrix[0].length;//列数
    int[][] ans = new int[col][row];
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            ans[j][i] = matrix[i][j];
        }
    }
    return ans;
}

解法二：一维表示 + 模拟

对于一个行数为row，列数为col的二维矩阵转换为一维矩阵表示，其索引值具有一定的映射关系：[i,j] -> [i * row + j]，这是线性代数的数学性质，对于任意索引都成立，不会因为从0开始而失效

public int[][] transpose2(int[][] matrix) {
    int row = matrix.length;//行数
    int col = matrix[0].length;//列数
    int[][] ans = new int[col][row];
    for (int i = 0; i < row * col; i++) {
        ans[i / row][i % row] = matrix[i % row][i / row];
    }
    return ans;
}