前言
本篇介绍栈和队列,了解栈有顺序栈和链式栈,队列底层是双链表实现的,单链表也可以实现队列,栈和队列的相互实现和循环队列;如有错误,请在评论区指正,让我们一起交流,共同进步!
文章目录
- 前言
- 1. 栈的认识
- 1.1 栈的使用:栈实现队列
- 2. 队列的认识
- 2.1 双队列实现栈
- 2.2 循环队列 - 数组实现的队列
- 3. 双端队列
- 总结
本文开始
1. 栈的认识
栈:一种特殊的线性表,只能从一头进入,一头出;
进出栈规则:先进后出
栈的模拟实现:顺序栈和链式栈实现栈时间复杂度都是O(1)
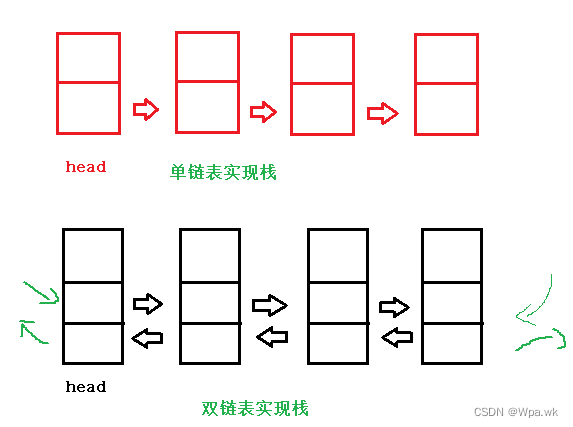
顺序栈:栈可以使用顺序表实现
链式栈:可以用单链表实现:头插和头删(入栈) 或 尾插和尾删(出栈);
可以使用双链表实现;既可以头进头出,也可以尾进尾出;(双链表知道前后节点位置)
链式栈代码实现:
public static void main(String[] args) {
//链表实现栈:LinkedList底层是双链表
LinkedList<Integer> stack = new LinkedList<>();
stack.push(1);
stack.push(2);
stack.push(3);
System.out.println(stack.pop());
}
代码实现栈的基本操作:
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
//压栈:栈中添加元素
stack.push(2);
stack.push(3);
//看栈顶元素
System.out.println(stack.peek());
//栈的大小
System.out.println(stack.size());
//出栈
System.out.println(stack.pop());
//栈是否为空
System.out.println(stack.isEmpty());
}
1.1 栈的使用:栈实现队列
双栈实现队列代码:
思路:
一个栈1表示入队,一个栈2表示出队;
队列出队需要判断栈2是否为空,栈2空将栈1中元素全部放到栈2中,此时再出栈2栈顶元素即可;
入队:看栈2是否有元素,栈2有元素直接返回栈顶元素;栈2为空,再将栈1中元素放到栈2中,才能看到出队的值;
public class MyQueue {
Stack<Integer> stack1;
Stack<Integer> stack2;
//创建两个栈
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
//在栈1中放元素
public void push(int x) {
stack1.push(x);
}
public int pop() {
if(empty()) {
return -1;
}
//判断栈2中是否有元素
if(stack2.isEmpty()) {
//栈1元素全部放到栈2中
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
//不空,栈2中有元素直接弹出
return stack2.pop();
}
public int peek() {
if(empty()) {
return -1;
}
//看栈2是否有元素
if(stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
//栈2有元素
return stack2.peek();
}
//判断两个栈是否为空
public boolean empty() {
return stack1.isEmpty() && stack2.isEmpty();
}
}
2. 队列的认识
1.队列:也是一种特殊的线性表,一头进,另一头出;
进出队列规则:先进先出;
2.链表实现队列:
单链表实现队列两种方式: - ==使用一种下标
头插法:进队-时间复杂的O(1) - 头插 ,出队-时间复杂的O(n) - 尾删
尾插法:进队-时间复杂的O(n) - 尾插,出队-时间复杂的O(1) - 头删
(两个下标控制头尾)单链表实现队列代码实现:
思想:使用头删尾插,进队出队时间复杂都是O(1);使用两个下标,记录头节点位置head,再记录尾节点位置last; 方便头插(入队),尾删(出队);
【注】单链表实现队列只能尾插头删,保证时间复杂度都为O(1)
不使用头插尾删原有?
使用头插尾删进行单链表,进队-头插时间复杂度O(1), 出队-尾删时间复杂度O(n);
尾删:每次删除都需要找尾节点前一个节点位置,需要遍历一般链表所以时间复杂度高;
代码:
public class MyQueue {
static class Node {
int val;
Node next;
public Node(int val) {
this.val = val;
}
}
//用双下标实现队列,需要定义两个
public Node head;//头下标
public Node last;//尾下标
public int size;
//入队操作: 插入
public boolean offer(int val) {
//插入需要新节点,创建新节点
Node node = new Node(val);
//没有节点的时候
if(head == null) {
//头尾下标指向同一位置
head = node;
last = node;
}else {
//head != null
//链接新节点
last.next = node;
//尾节点向后移动一步
last = node;
}
size++;//计数
return true;
}
//出队:删除头删
public int poll(int val) {
//判断链表是否为空
if(isEmpty()) {
return -1;
}
//记录删除的值
int v = head.val;
head = head.next;
//如果只有一个节点,lasta也需要置空
if(head == null) {
last = null;
}
size--;//-1
return v;
}
private boolean isEmpty() {
return size == 0;
}
public int peek() {
//链表为空不用看队头元素
if(isEmpty()) {
return -1;
}
return head.val;//返回队头元素
}
public int getSize() {
//队列大小
return size;
}
}
双链表实现队列代码实现:
特点:双链表实现队列可以自由头进尾删,头删尾进;
public class MyQueue2 {
//双链表实现队列
static class Node {
int val;
Node prev;
Node next;
public Node(int val) {
this.val = val;
}
}
//前后下标
public Node front;
public Node last;
public int size;
//入队
public boolean offer(int val) {
//插入的新节点
Node newNode = new Node(val);
//没有节点
if(front == null) {
front = newNode;
last = newNode;
}else {
//不为空
//链接前后节点
newNode.prev = last;
last.next = newNode;
//后下标后移
last = newNode;
}
size++;
return true;
}
//出队:删除
public int poll() {
int v = -1;
//队列为空
if(isEmpty()) {
return -1;
}
//只有一个节点
if(front == last) {
front = null;
last = null;
}else {
//先记录值
v = front.val;
//前下标后移
front = front.next;
//找到前一个下标的next置为空
front.prev.next = null;
//当前prev置为空:防止空指针异常
front.prev = null;
}
size--;
return v;
}
private boolean isEmpty() {
return size == 0;
}
public int peek() {
if(isEmpty()) {
return -1;
}
return front.val;
}
}
队列基本操作代码实现:
public static void main(String[] args) {
Queue<Integer> queue = new LinkedList<>();
//入队:队列中添加元素
queue.offer(1);
queue.offer(2);
queue.offer(3);
//看队头元素
System.out.println(queue.peek());
//队列的大小
System.out.println(queue.size());
//出队
System.out.println(queue.poll());
//队列是否为空
System.out.println(queue.isEmpty());
}
2.1 双队列实现栈
双队列实现栈:
思路:
①先定义两个队列
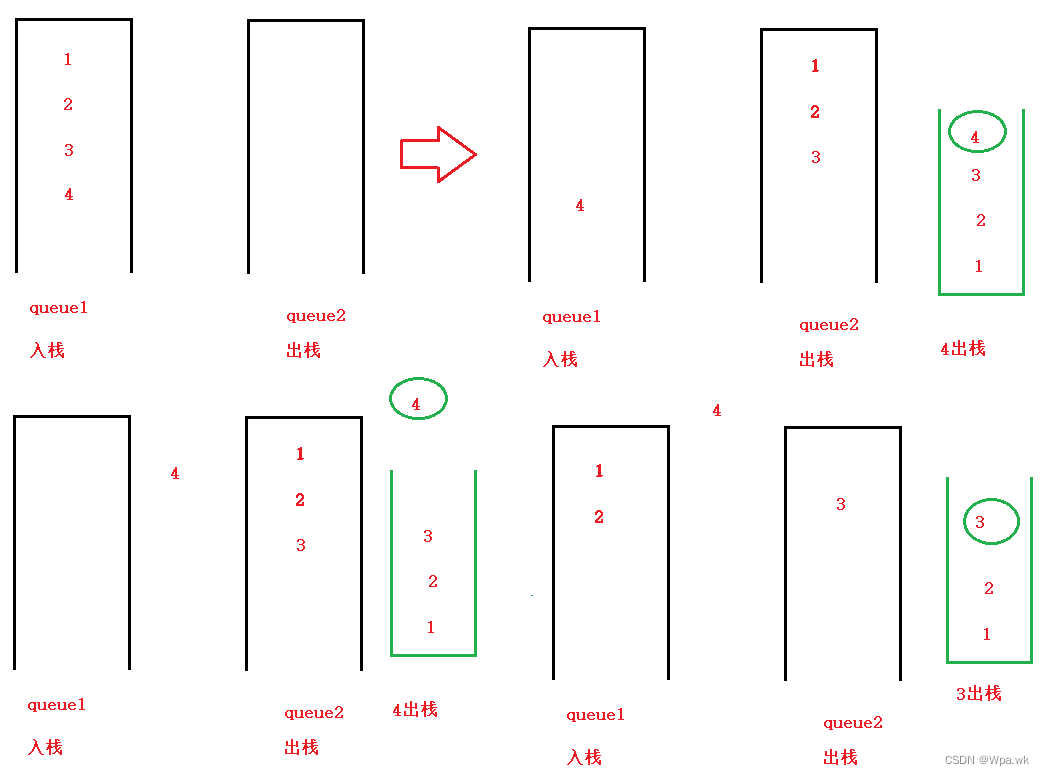
②入栈:是判断那个队列不为空,队列1不为空,就往队列1中放,队列2不为空,就往队列2中放,都为空默认往队列1中放;
③出栈:假设不为空队列元素个数为size个,将不为空的队列出队size-1个到另一个为空的队列,出队列size-1个队列剩余一个就为出栈元素;
④栈顶元素:假设队列1不为空,队列2空;定义一个变量为tmp, 作为队列1元素到队列2元素的过度,将队列1中元素全部传到队列2中,此时队列1最后出队的元素就是栈顶元素,并存储在tmp中,返回tmp即可;
代码实现:
import java.util.LinkedList;
import java.util.Queue;
public class MyStack {
//双队列实现栈
//构建双队列
Queue<Integer> queue1;
Queue<Integer> queue2;
public MyStack() {
queue1 = new LinkedList<>();
queue2 = new LinkedList<>();
}
public void push(int x) {
//两个对谁不为空,就入那个队
if(!queue1.isEmpty()) {
queue1.offer(x);
}else if(!queue2.isEmpty()) {
queue2.offer(x);
}else {
//都为空,入第一个队
queue1.offer(x);
}
}
public int pop() {
//判断队列是否为空
//都为空
if(empty()) {
return -1;
}
if(!queue1.isEmpty()) {
//获取队列1大小
int size = queue1.size();
//队1出size-1个元素,到队2中
while (size - 1 != 0) {
queue2.offer(queue1.poll());
size--;
}
//队1只剩1个,就是要出栈的元素
return queue1.poll();
}else {
//队1为空,队2不为空
//获取队列2大小
int size = queue2.size();
//队2出size-1个元素,到队1中
while (size - 1 != 0) {
queue1.offer(queue2.poll());
size--;
}
//队2只剩1个,就是要出栈的元素
return queue2.poll();
}
}
public int top() {
//判断队列是否为空
//都为空
if(empty()) {
return -1;
}
if(!queue1.isEmpty()) {
//获取队列1大小
int size = queue1.size();
int tmp = -1;//存储每个出队元素
while (size != 0) {
tmp = queue1.poll();
queue2.offer(tmp);
size--;
}
//队1最后一个出队的,就是要栈顶的元素
return tmp;
}else {
//获取队列2大小
int size = queue2.size();
int tmp = -1;//存储每个出队元素
while (size != 0) {
tmp = queue2.poll();
queue1.offer(tmp);
size--;
}
//队2最后一个出队的,就是要栈顶的元素
return tmp;
}
}
public boolean empty() {
return queue1.isEmpty() && queue2.isEmpty();
}
}
2.2 循环队列 - 数组实现的队列
循环队列:可以看成一圈型的队列,但其实还是数组
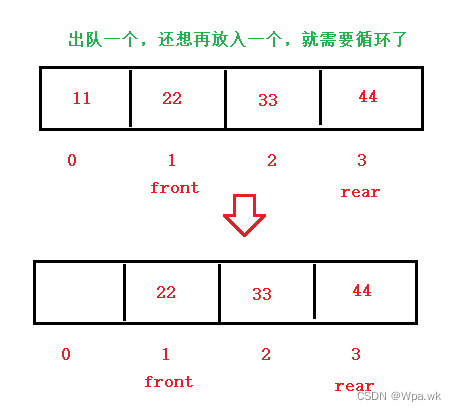
为什么使用循环?
一个存满的数组,先出队一个,如果再进队尾rear下标就越界了,但数组中还有空间没有利用 =》 对于这种情况所以使用了循环;
怎么实现循环?
1.可以使用下标标记法,进队一个标记一个,从而实现循环;
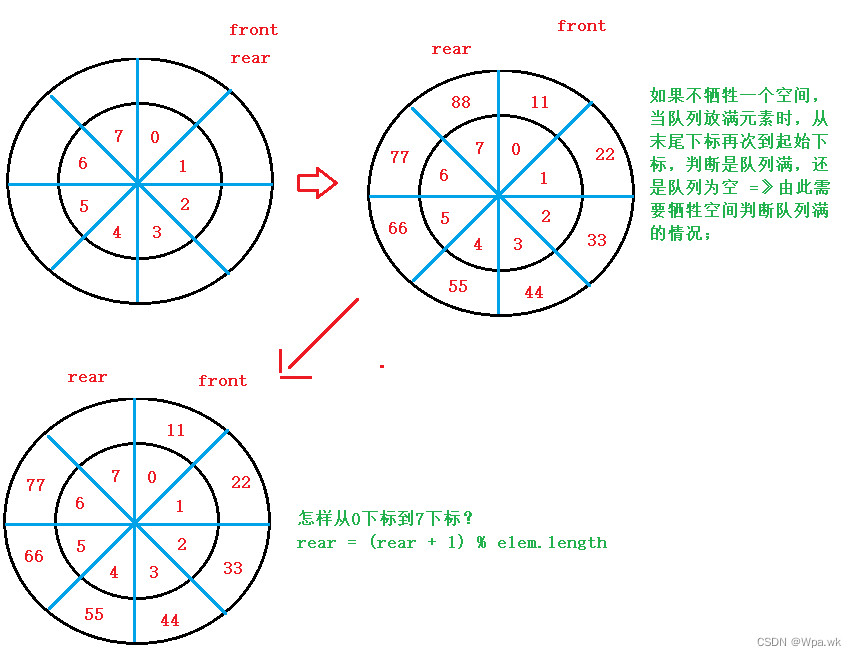
2.牺牲一个空间,使用求余来实现循环 ( rear + 1) % length;(循环需要首尾相连,如图从7下标到0下标,求余就可以实现;)
实现循环队列:
思路分析:
判断循环队列是否为空还是满,就使用牺牲一个空间法,(rear + 1) == front 判断为满;
rear == front 判断为空;如下图
怎样实现循环:使用求余数的方法,可以让下标从尾下标到开始下标(如图0下标到7下标);
循环队列代码:
class MyCircularQueue {
//循环链表:底层是数组,所以创建数组
int[] elem;
//循环的前后下标
int front;//前
int rear;//后
public MyCircularQueue(int k) {
//初始化k大小的数组
elem = new int[k + 1];
}
//进队
public boolean enQueue(int value) {
//进队先判断队列是否满
if(isFull()) {
return false;
}
//不满进队
elem[rear] = value;
//rear++ =》不能使为下标到起始下标,进行循环,所以使用求余数;
rear = (rear + 1) % elem.length;
return true;
}
//出队
public boolean deQueue() {
//出队先判断队列是否有元素
if(isEmpty()) {
return false;
}
//前下标+1,与需要考虑构成循环,末尾到开始位置
front = (front + 1) % elem.length;
return true;
}
//获取队头元素
public int Front() {
if(isEmpty()) {
return -1;
}
return elem[front];//不为空就返回
}
//获取队尾元素
public int Rear() {
if(isEmpty()) {
return -1;
}
//牺牲一个空间法,尾下标超过尾元素1个数组空间 =》所以一般情况:尾下标需要-1才是尾元素
//会遇到一种尾下标在(0位置)起始位置,而尾元素在最后位置,需要构成循环 =》 这里特殊情况,特殊出来0下标位置
int index = (rear == 0) ? elem.length - 1 : rear - 1;
return elem[index];
}
//判断是否为空
public boolean isEmpty() {
return rear == front;
}
//判断是否满
public boolean isFull() {
//循环队列使用牺牲1个空间方法,区分空和满
//rear+1 再余 =>构成循环,尾下标就能够到起始下标;
return (rear + 1) % elem.length == front;
}
}
3. 双端队列
双端队列:是一种继承Queue的接口,可以用它实现栈与队列;
实现栈,队列:
Deque<Integer> stack1 = new ArrayDeque<>();
Deque<Integer> stack2 = new LinkedList<>();
Deque<Integer> queue1 = new LinkedList<>();
总结
✨✨✨各位读友,本篇分享到内容如果对你有帮助给个👍赞鼓励一下吧!!
感谢每一位一起走到这的伙伴,我们可以一起交流进步!!!一起加油吧!!!