Routability-Driven Macro Placement with Embedded CNN-Based Prediction Model
2019 Design, Automation & Test in Europe Conference & Exhibition (DATE)
DOI: 10.23919/DATE.2019.8715126

Abstract
一、Introduction
二、PROBLEM FORMULATION AND PRELIMINARIES
- 2.1 Problem Formulation
- 2.2 Convolutional Neural Network
- 2.3 Transfer Learning
三、MACRO PLACEMENT WITH EMBEDDED ROUTABILITY PREDICTION MODEL
- 3.1 Feature Extraction
- 3.2 Routability Prediction
- 3.3 Simulated Annealing Optimization
四、EXPERIMENTAL RESULTS
- 4.1 Routability Prediction
- 4.2 Simulated Annealing Optimization
总结与思考

Abstract

一个芯片设计只有通过设计规则检查(DRC)后才能被贴出。设计复杂度严重恶化了设计可路由性，这可以用详细路由阶段之后的DRC违规次数来衡量。此外，由于知识产权的广泛使用，现代大型设计通常由许多巨大的宏组成。根据经验，宏的布局在很大程度上决定了可路由性，但由于单元布局和路由的复杂性和不可预测性，目前还没有一个有效的成本指标来直接评估宏布局。在本文中，我们提出了第一个基于深度学习的宏布局方法RoutabilityDriven。提出了一种基于卷积神经网络(CNN)的可布线性预测模型，并将其嵌入到宏布线器中，通过模拟退火(SA)优化过程可以得到一个具有最小DRC违规的良好宏布线。

一、Introduction

在这里插入图片描述

现代大型设计通常由许多巨大的宏组成。宏的数量急剧增加，这些巨大的宏可以占据芯片面积的70%以上。从经验上看，宏的放置在很大程度上决定了可路由性，这可以从图中显示的示例布局中观察到，Fig. 1(a)和(b)给出了同一电路的两个不同宏位置。 ©和(d)分别给出了两个宏布局在单元布局和路由之后的布局，这两个布局是由商业EDA工具Enceence完成的。白色表示DRV的位置，这是由违反DRC规则的路由网络造成的，如短路和间距违规。据实验结果，在Fig.1©有4892次违规，而在图的布局 Fig.1(d)有65868次违规，这清楚地表明宏放置对设计可路由性有很大的影响。在现代大规模设计中，单元布局和布线通常需要很长的时间，因此，在运行整个设计流程后，枚举给定设计的所有宏布局并找到最佳的宏布局是不现实的。

在这里插入图片描述

许多关于宏布局的研究已经被提出来解决这些设计挑战，这些研究可以分为三类：
（1）同时放置宏和标准单元的一阶段混合尺寸布局；例如:MPL6[12]，Ntuplace3[9]，Hsu等。 [14]、Complex[17]、Maple[18]、ePlace-MS[19]和FastPlace3.0[27]。
（2）构造型MixedSize宏布局，在迭代过程中对宏进行划分并保持宏不重叠；例如，CAPO[1]和FLOP[28]。（3）三阶段混合尺寸布局，包括布局原型、宏布局和标准单元布局，如图所示 2；例如，XDP[10]，CG[8]，Floorist[21]，MP-Tree[11]，CP-Tee[7]，Chiou et al[5]。

三阶段方法由于其更好的性能和易于集成到大多数设计流程中而受到广泛的关注。最近，MP-tree被提出来有效地打包宏[11]。 CP-tree继承了MP-tree的优点，并考虑了预置块[7]。由于上述两种表示方法在处理宏重叠方面存在不足，本文提出了一种基于圆轮廓的基于角点序列的宏布局方法[20][5]。然而，所有的三阶段宏观放置依赖于从一阶段混合尺寸放置生成的放置原型。放置原型步骤不仅需要更多的运行时间来执行附加步骤，而且还可能导致以下方面的一些缺陷：

如果初始的宏合法那么变化的空间有限，如果不合法布线变得不可控，宏放置可能不是最优。
由于放置器根据宏在原型中的位置估计线缆和布线成本，并在目标函数中最小化宏与原型的位移，因此最终的宏放置可以与原型中的宏放置非常相似。换句话说，原型可能会限制优化解空间，成为决定优化宏布局轮廓的主要因素。相反，如果将宏位移设置为目标函数中的次要优先级，使得宏放置器更灵活地生成显著不同的宏放置，则线形和可布线性估计变得不准确，并且生成的宏放置可能不是最优的。
现有的模型针对单元布局和局部路由，不适应宏布局阶段。
由于单元布局和路由的高度复杂性和不可预测性，没有有效的代价度量来直接评估宏布局，宏布局是一个可以合理地求助于机器学习的优化问题。在物理设计过程中，已经有几个关于DRV预测的工作。其中一些通过考虑全局路由或试路由后的拥塞图来预测给定小区位置的DRV和拥塞区域的数量[23]，[29]。然而，由于高级过程节点的设计规则越来越复杂，导致拥塞图与最终DRV图之间的不相关性[4]、[6]。为了避免被不适当的特性所误导，并节省全局/试验路由的运行时间，其他的工作试图在没有拥塞映射的情况下预测布局的可路由性[4]、[6]、[25]、[26]。 [25]和[26]开发基于机器学习的方法来预测布局瓦片中是否发生短违规。 [6]提出的模型预测一个布局解是否可路由。 [4]提出了一种基于支持向量机(SVM)的DRVs位置预测方法。然而，所有这些工作都是针对给定的单元布局进行局部可路由性预测，现有的模型不适用于宏布局阶段。

在本文中，提出了可路由驱动的宏布局与深度学习。一种基于卷积神经网络(CNN)的可布线型预测模型，并嵌入到一个宏布局中的I预测模型，通过模拟退火(SA)优化过程可以得到一个具有最小DRC违规的良好宏观布局。本文的主要贡献如下:

首次将机器学习应用于宏观布局阶段的可路由性预测。构建了可路由性预测器来预测DRV的数量。预测模型的输入只需要一个宏布局，不需要单元布局和路由信息。
采用迁移学习方法解决训练数据不足的问题。使用预训练的VGG16[24]体系结构，并用我们的宏放置数据集进行微调。
将开发的基于机器学习的可路由性预测器嵌入到宏布局中。此外，利用模拟退火优化算法，以最小的DRVs搜索最优的宏布局。
实验结果证明了预测模型的准确性和我们的可路由性驱动宏布局的有效性。

第二节介绍了问题的提出和CNN的初步研究。在第三节中，建议的模型开发和宏观放置方法在每个小节中都有详细说明。第四节给出了实验结果。最后，我们在第五节结束我们的工作。

二、PROBLEM FORMULATION AND PRELIMINARIES

2.1 Problem Formulation

我们的工作目标是解决两个问题：（1）给定宏观布局的早期可路由性预测；（2）在设计规则违反最小的情况下寻找最佳的宏布局。

问题1： 在第一个问题中，任务是找到一个预测给定宏布局的DRVs（表示为#DRVs）数量的模型，该模型可以表示为函数f#DRVs如下:

$f_{\# D R V s}: S_i \in \mathbb{R}^{W \times H} \rightarrow y_i \in \mathbb{N}$ （1）

其中，放置的宏 $S_i \in \mathbb{R}^{W \times H}$ ，其中W和H表示放置平面的宽度和高度。我们的目的是找到一个最优函数 $f_{\# D R V s}^*$ 使得 $f_{\# D R V s}$ 最小。

$f_{\# D R V s}^*=\underset{f}{\arg \min } \operatorname{Loss}\left(f_{\# D R V s}\left(S_i\right)-y_i\right)$ （2）

问题2： 在第二个问题中，输入 $P_i$ 是由宏、标准单元和芯片区域W×H组成的布局实例。我们的目标是找到一个设计的宏布局 $S_i$ ，在单元布局和布线后，预测的#DRVs最小化；也就是说，使用以下目标函数执行宏放置：

$\min f_{\# D R V s}^*\left(S_i\right) \mid S_i \in \mathbb{R}^{W \times H}$ (3)

2.2 Convolutional Neural Network

CNN是一个神经网络，它是一个相互连接的人工神经元系统，具有卷积运算和相互交换信息。在训练过程中调整连接的数值权重。 CNN在许多不同的研究领域得到了广泛的应用。图 3是用于图像处理的通用CNN体系结构。典型的CNN是由卷积层、池层和全连通层组成的前馈网络。
在这里插入图片描述

2.3 Transfer Learning

迁移学习在机器学习领域得到了广泛的应用，它将知识从一个已研究过的问题转移到一个不同但相关的问题[22]。由于当可用的数据集不足以训练一个完整的网络时，从零开始训练一个模型（随机初始化）是非常困难的，所以使用一个已经用大量数据集训练过的现有网络（如ImageNet[13])，并用目标任务的有限数据集对其进行微调是更现实的。在我们的工作中，为了预测#DRVs，需要完成整个设计流程才能得到最终的路由结果，因此获取大量的训练数据极其耗时。表I显示了从2015 ISPD基准[2]生成每个电路的单个训练数据的平均运行时间（以秒为单位），其中gp、dp、gr和dr分别表示全局布局、详细布局、全局路由和详细路由。从表中可以观察到，生成一个数据需要7-38分钟。因此，我们采用VGG网络结构作为CNN模型的基础，并在合理的时间内利用有限的训练数据对其进行微调[22]。

三、MACRO PLACEMENT WITH EMBEDDED ROUTABILITY PREDICTION MODEL

3.1 Feature Extraction

在这里插入图片描述

在本工作中，宏布局的可路由性是由小区布局和路由后的DRVs来量化的，因此需要一个CNN模型来准确地预测给定宏布局的DRVs的数量。作为CNN模型的输入，我们把一个宏布局的布局看作是一个三维的张量，由二维特征映射堆叠而成。本工作中使用的三个特征图如下:

宏密度图：给定由宏放置器生成的宏位置，宏的位置是固定的，因此可以通过计算每个像素的宏覆盖率来导出密度图。
针密度图：在宏放置阶段，单元的位置是未定的。因此，只计算宏管脚的密度分布。
连通性映射：宏引脚的连通性表示连接到该引脚的网络数量。连通性映射给出了宏管脚在相应像素处的连通性。

图 6说明了作为CNN模型输入的三个二维特征图。通过计算一个宏布局 $S_i$ 的三个特征，独立生成尺寸为W×H的三个特征映射。之后，将这三个特征映射叠加，构造出一个三维输入张量 $X_i∈R^{W×H×3}$ 。注意，特征规范化应用于每个特征映射。这是因为如果特征映射之间存在较大的差异，某些特征可能对训练模型产生确定性影响，而另一些特征则不会。因此，我们将每个特征映射归一化，使其值介于0和1之间。归一化也有助于训练模型更快的收敛。

3.2 Routability Prediction

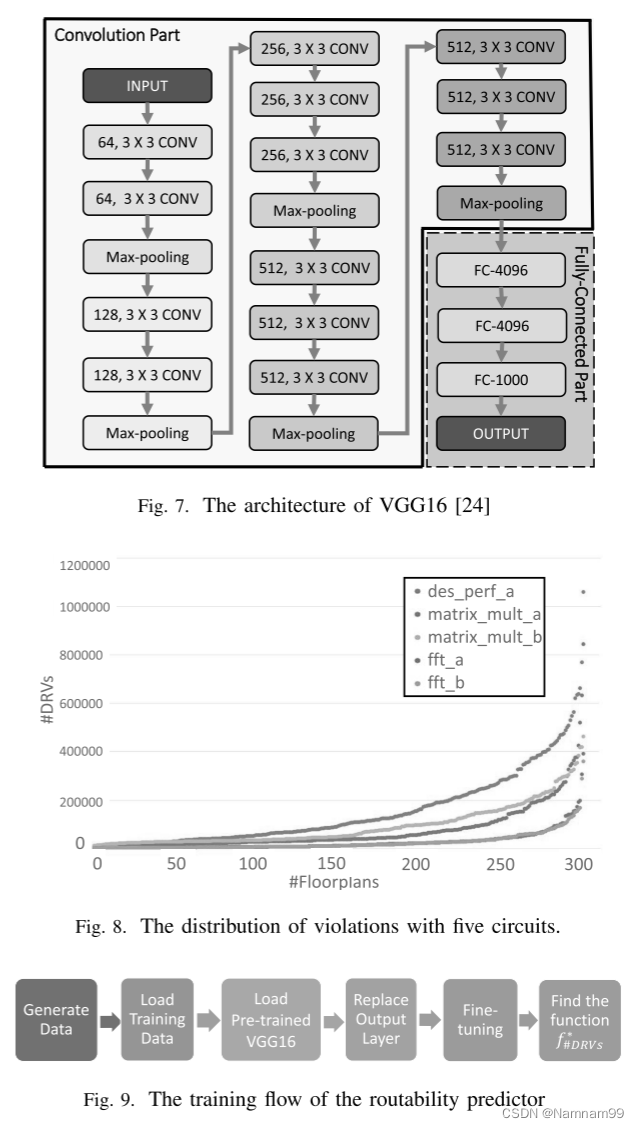
在这里插入图片描述
如2.3节所述，由于训练数据不足，我们采用迁移学习来训练我们的预测模型。我们的工作采用了深度卷积神经网络VGG16，其中“16”表示配置的深度。图 7给出了VGG16的体系结构，它可以分为两个部分：卷积部分和全连接部分。卷积部分由卷积层和MaxPooling层叠加而成，每个卷积层中的“m,n×n conv”表示该层使用了m，n×n滤波器。在完全连接的部分，完全连接层中的神经元与前一层中的所有激活都有完全连接。最后，VGG16输出1000个浮点值，每个浮点值是输入图像属于1000个类之一的概率。
为了生成所需的数据，实现一个宏放置方案以导出一组不同的宏放置，而EDA工具Access被用于单元放置和路由[3]。在设计规则检查后，报告每个案例的#DRVs。生成的宏放置是我们的训练数据和测试数据，对应的#DRV作为标签。由于VGG16的输入图像的维数固定为224×224，每个输入张量 $X_i∈R^{W×H×3}$ 被重塑为 $X_i∈R^{224×224×3}$ 。

此外，标签还被缩放，使得它们的值落在1和m之间，其中m是用户定义的数字。主要原因可以用图8来解释:

其中对每个电路的300个案例的#DRVs进行排序和绘图。从图中可以看出，在不同的电路中，#DRVs的分布非常不同，这是可以理解的，因为较大的电路通常比较小的电路遭受更多的DRVs。这一现象意味着用单一的预测模型对所有电路进行精确的#DRVS预测是困难的。
考虑到宏观砂矿的目标，找到一个相对较低的#DRVs的良好宏观布局比准确预测实际DRVs数量更重要。因此，标签（即#DRVs）首先被缩放到[1，m]，使得该模型可以适用于任何输入电路。图 9展示了可路由性预测器的训练流程。

数据准备完毕后，加载预训练的VGG16模型。由于我们的训练数据量相对较小（与用于训练VGG16的ImageNet相比），我们固定了VGG16中图像处理能力较强的卷积部分，只对全连接部分进行微调。我们将输出层从一个1000类分类器替换为一个回归器，该回归器输出一个表示缩放的#DRVs的单个数字。所有隐层都配有激活函数整流线性单元(RELU)[15]。采用均方对数误差(MSLE)作为损失函数，用ADAM进行优化[16]。此外，卷积操作会使输入图像收缩，而由于宏通常放置在靠近边界的地方，因此丢失芯片边界信息是不可取的。因此，采用填充，使输出具有相同的尺寸作为原始输入。此外，以差分率0.25设置差分层以防止过拟合。

3.3 Simulated Annealing Optimization

我们工作的最终目标是为给定的电路找到预测的#DRVs最少的最佳宏位置。因此，我们将3.3建立的预测模型嵌入到一个宏观放置中，并应用模拟退火(SA)算法全局搜索最优解。我们实现了基于圆轮廓的宏放置器，它使用角点序列[20] 作为 宏放置的表示[5]。给定当前解的一个角序列CS，在SA:

OP1:交换CS中的第i和第j个宏时采用三种扰动操作。
OP2:在CS中的第j个宏之后插入第i个宏。
OP3:为每个宏分配不同的角。迭代地执行扰动操作，直到导出合法的宏布局。

在推导出宏观布局 $S∈R^{W×H}$ 的新解后，将其重塑张量 $X∈R^{224×224×3}$ 输入预测模型。如果S’的预测的#DRVs小于前一个解决方案S的#DRVs,则S’将被接受。相反，如果S’比S差，则S’也可以被接受。输出将是SA算法在满足终止条件之前找到的最佳宏布局。

四、EXPERIMENTAL RESULTS

对于每个电路，我们使用所实现的宏放置器生成至少300个显著不同的宏放置，并保证每个电路类型的600个宏放置。然后，利用EDA工具Cadence Encure完成单元布局和路由[3]，并以DRC后报告的DRV数作为标记。

4.1 Routability Prediction

预测方案的与真实的基本吻合
为了验证所提模型的预测能力，对其中四个电路进行了训练，并对另一个电路进行了测试。这就保证了测试电路是对训练过的机器学习模型的一种隐形设计，以满足工业中处理许多新的隐形设计的要求。我们将每个测试电路的所有宏布局按其真的#DRVs升序排序，表示为T，我们还将宏布局按其预测的#DRVs升序排序，表示为P。由于我们对机器学习模型预测的那些顶级宏布局（带有较少的#DRVs）是否真的是好的解决方案感兴趣，我们报告了P的前N个宏布局中的最佳真秩。可以观察到，每个电路的第1或第2最佳宏放置可以被预测器在其Top-30候选中找到，大多数可以在Top10或Top-20候选中找到。结果表明，该预测器在可路由性方面具有一定的预测宏布局质量的能力。

4.2 Simulated Annealing Optimization

我们将可路由性预测器嵌入到所实现的宏布局器中，并使用基于SA的优化方法来寻找具有最少的DRVs的最佳宏布局。为了进行比较，我们在没有嵌入模型的情况下实现了一个基于基线圆形轮廓的宏配置方案[5]。由于我们的工作没有考虑布局原型，所以在SA优化过程中，我们只考虑边界代价来实现基线宏Placer，从而使Placer专注于为标准单元保留更多的空间和路由区域的完整性。由于随机方案，我们重复执行基于SA的优化，为每个电路以及我们的方案和基线方案获得100个宏位置。将得到的#DRVs与开始时生成的数据集进行比较，用于模型训练和测试。请注意，由于Acception许可证最近发生了变化，只为小于100K单元的学术设计提供服务，因此在本实验中只测试了两个较小的电路，因为它是在此之后进行的。表IV显示了两个宏放置器的解决方案质量，其中“top-y”列中的x%报告了解决方案质量与数据集的top-y宏放置相当的宏放置的百分比。根据表IV，基准砂矿生成的FFT A与数据集的Top-10、Top-20和Top-30的宏放置率分别只有2%、22%和34%，而我们砂矿的解与数据集的Top-10、Top-20和Top-30的宏放置率分别为75%、82%和84%。在FFT b的统计中也可以发现类似的趋势。

此外，FFT A和FFT B的34%和24%的宏观位置甚至比数据集中最好的宏观位置更好，这表明训练的可路由性预测模型的预测能力有助于找到数据集中从未见过的更好的解。分别从我们的砂矿和基准砂矿中获得的最佳宏观位置（最少的DRVs）的布局见图4(a)和(b)。在完成单元布局和路由之后，基线宏布局导致2426个违规，而我们的宏布局只产生851个违规。此外，平均总wirelength(TWL)和平均运行时间也在表四中报告。对于这两个电路，我们的方案与基准方案相比，分别可以实现9.16%和5.35%的TWL降低，这应该是由于宏放置的更好的可布线性。注意，我们的Placer需要更多的运行时间来进行可路由性预测，在每个SA迭代中执行位置重塑、特征提取和CNN推断。然而，不仅运行时开销是可以接受的，而且所提出的流可以从运行整个后端流到只运行其中几十个宏，大大节省总体设计时间。