文章目录
- 前言
- 排序模板
- 排序算法
- 归并排序
- KMP
- 图
- 邻接表
- Floyd 算法
- Dijkstra
- BellMan-Ford 算法
- SPFA 算法
- Prim 算法
- Kruskra 算法
- 染色法
- Hunger算法
前言
翻了翻自己以前写的一些博文,发现的话,还是有一些误区没有写好的,所以的话这里的重新写一下,然后的话,这里的话我们就直接提供Python版本的一个代码,C++ 的先前的博文都有了,那么这篇博文的话也是这个代码颇多,所以的话,对记忆的要求较高。刚好也挑战一下自己对于这些代码的一个牢固程度吧。
当然由于这些篇幅所限,这里的常见模板还是非常简单入门的东西,当然如果这篇博文对你有所帮助的话,请不要吝啬你的三连~
排序模板
首先是关于排序的模板,这个的话,我这里就是直接给出两个排序算法的模板,一个是快速排序,这个玩意的特点就是快,缺点就是不稳定,那么如何解决稳定问题,为什么这个快速排序是不稳定的,这个原因的话,咱们以前也是有写博文进行分析过的,所以的话这里就不再复述了。那么第二个算法就是这个归并排序的模板,这个算法也不慢,并且这个算法是稳定的。虽然有时候比赛的时候我们可能是直接调用现成的这个排序工具包,但是还是得写写的。
那么在开始之前的话,我们先定义一下我们的这个数据,首先我们这边要进行排序的数组是a,l,r 分别是0和len(a)-1,此外的话我们还有一个temp数组,这个数组的长度是和a一样的,在归并排序的时候需要使用到
排序算法
OK,那么在这里的话是我们的排序算法。
def quick_sort(a,l,r):
if(l>=r):
return
key = a[l]
i,j = l-1,r+1
while(i<j):
i+=1
j-=1
while(a[j]>key):
j-=1
while(a[i]<key):
i+=1
if(i<j):
temp = a[i]
a[i] = a[j]
a[j] = temp
quick_sort(a,l,j)
quick_sort(a,j+1,r)
归并排序
那么接下来就是我们的这个归并排序了
def merge_sort(a,temp,l,r):
if(l>=r):
return
mid = (r+l)//2
merge_sort(a,temp,l,mid)
merge_sprt(a,temp,mid+1,r)
k = 0
while(i<=mid and j<=r):
if(a[i]<a[j]):
temp[k] = a[i]
i+=1
else:
temp[k] = a[j]
j+=1
k+=1
while(i<=mid):
temp[k] = a[i]
k+=1
i+=1
while(j<=r):
temp[k] = a[j]
j+=1
k+=1
k = 0
i = l
while(i<=r):
a[i] = temp[k]
k+=1
i+=1
KMP
那么接下来是比较出名的KMP算法,这里的话其实有一个比较有意思的算法,叫做Sunday算法,感兴趣的可以自己去了解一下,这个算法的话,用来做字符串匹配是非常有意思的。那么本文从KMP算法开始,接下来就是图相关的算法了,那么这些算法无一例外都和KMP算法一样运用了这个DP的思想。(DP+数论 干翻友商)
那么关于KMP的话,同样的,这个咱们以前也是有分析过的,当时好像还给出了一个关于KMP的一个逻辑推理。这里的话关于next数组当时应该忘记说了,那就是这个求取next的数组为什么和那个匹配的时候的算法那么像,其实的话在找到那个那个我写的关于KMP逻辑推理的一个说明,其实是可以发现,next找的其实就是自己和自己可以匹配的部分,所以代码很像,然后呢,在求解这个next数组的时候运用DP思想。
def getNe(s):
"""
求取next数组
"""
m = len(s)
#数组取大一点是没有关系的
next = [0 for _ in range(m+10)]
i = 1
j = 0
while(i<m):
while(j>0 and s[i]!=s[j]):
j = next[j-1]
if(s[i]==s[j]);
j+=1
next[i] = j
i+=1
return next
def KMP(s1,s2):
"""
返回第x个字符之后会匹配上
"""
next = getNe(s2)
m_s1 = len(s1)
m_s2 = len(s2)
i = 0
j = 0
while(i<m_s1):
while(j>0 and s1[i]!=s2[j]):
j = next[j-1]
if(s1[i]==s2[j]):
j+=1
if(j==m_s2):
return i - m_s2 + 1
i+=1
return -1
图
okey,接下来的大部分算法就是关于这个图的算法了。
那么同样的,这里有好几种算法,以及图/树 的两种存储方式,邻接表和领接矩阵。 关于邻接矩阵这个自然是没有什么好说的,懂得都懂,那么这块的主要是这个邻接表。
那么这个邻接表的话采用的方式就是咱们算法导论里面说的那种:
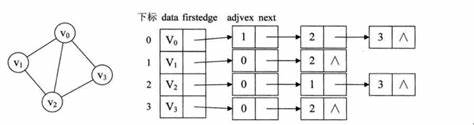
所以的话我们在这块将使用到这几个玩意,接下来我会重新解释一下这几个玩意,当时没有解释好,有几个误区,这里的话我检讨一下。ok,那么这里的话,我们开始定义一下,我们接下来会使用到的数据。
- n,m 首先我们假设我们所有的节点的编号是从1开始的,节点个数为n,边的个数为m
g = [[0 for _ in range(n)] for _ in range(n)]这里的话我们的这个列表表达式的速度是非常快的,同时不会存在引用的一些问题,所以建议使用Python时使用这个进行初始化。- ne ,w,e,h 这些都是列表,
ne = [0 for _ in range(n+m)]都是这种格式的,这里的话取n+m只是为了把这个列表搞大一点。h 的初始化的值为-1 :h = [-1 for _ in range(n+m)]
idx 用于记录这是第几条边
那么同时参考算法使用逻辑为:
邻接表
okey,那么接下来的话我们来解释一下这个关于邻接表的一写说明。
首先我们不妨来看到这个使用邻接表的时候,是如何插入数据的(这里的话是采用邻接表法)
def add(a,b,c):
e[idx] = b
w[idx]= c
ne[idx] = h[a]
h[a] = idx
idx+=1
okey,现在我开始解释了.
首先idx,表示的是输入存储的第几条边。我们在存入的时候是按照边进行存储的
e[idx] 表示存储的第idx条边,以a 为左端,b为右端的边,它的右端的节点是b
w[idx] 表示第idx条边的权重是c
ne[idx] 表示和第idx这条边,在与a相连的上一条边是啥,例如a–>c,a–>b ,这个时候a是和b,c直接相连的,并且是按照顺序输入的。那么ne[idx] = h[a] 表示的就是a–>c 这条边。然后的话,前面也说了是尾插法嘛,对吧
之后是h[a] 这个表示的就是当前最后输入进去的和a直接相连的边是第idx条边。
那么这个时候的话,我们按照这个边去寻找就好了
Floyd 算法
def Floyd(g):
for k in range(1,100):
for i in range(1,100):
for j in range(1,100):
g[i][j] = min(g[i][k]+g[k][j],g[i][j])
Dijkstra
接下来是Dijkstra 算法
def Dijkstra(g):
st = [False for _ in range(n+1)]
dist = [float("inf") for _ in range(n+1)]
dist[1] = 0
for i in range(n-1):
t = -1
for j in range(1,n+1):
if(not st[j] and (t==-1 or dist[t]>dist[j]):
t = j
for j in range(1,n+1);
dist[j] = min(dist[j],dist[t]+g[t][j])
if(dist[n]==float("inf")):
return False
BellMan-Ford 算法
那么这个算法的话,就比较随意了。那么这块的话定义一个新的数据结构用来存储这玩意
class node:
a = None
b = None
c = None
Nodes = [node(a,b,c) for _ in range(m)]
def BellmanFord():
dist = [float("inf") for _ in range(1,n+1)]
dist[i] = 0
for i in range(n):
for j in range(m);
a,b,w = Nodes[j].a,Nodes[j].b,Nodes[j].c
dist[b] = min(dist[b],dist[a]+w)
SPFA 算法
这个算法是一个非常有意思的算法,一般情况下,直接SPFA,最坏情况下就Dijkstra就好了。
那么这个算法的话对应的也是一个稀疏图的一个算法
def SPFA():
import collections
q = collections.deque()
dist = [float("inf") for _ in range(n)]
st = [False for _ in range(n)]
q.append(1)
st[1]=True
while(len(q)):
t = q.pop()
st[t] = False
i = h[t]
while(i!=-1):
j = e[i]
if(dist[j]>dist[t]+w[i]):
dist[j] = dist[t]+w[i]
if(not st[j]):
q.append(j)
st[j] = True
i = ne[i]
# 这个自己取一个比较大的数
if(dist[n]>=100000):
return False
除此之外的话,还有用这个算法来判断一个图当中是否存在负环的。
def SPFA2():
import collections
cnt = [0 for _ in range(n)]
q = collections.deque()
dist = [0 for _ in range(n)]
st = [False for _ in range(n)]
dist[1] = 0
for i in range(1,n+1):
q.append(i)
st[i] = True
while (len(q)):
t = q.pop()
st[t] = False
i = h[t]
while (i != -1):
j = e[i]
if (dist[j] > (dist[t] + w[i])):
# 这个其实就是DP
cnt[j] = cnt[t] + 1
dist[j] = dist[t] + w[i]
if(cnt[j] == 100):
# 为TRUE 说明有负环
return True
if (not st[j]):
q.append(j)
st[j] = True
i = ne[i]
return False
Prim 算法
那么之后的话就是这个最小生成树了。
这个算法是使用与稠密图的。
def Prime(g):
"""
这里的话还是使用邻接矩阵的
:return:
"""
dist = [float("inf") for _ in range(100)]
st = [False for _ in range(100)]
res = 0
for i in range(100):
t = -1
for j in range(1,101):
if((t == -1 and not st[j]) or dist[t]>dist[j]):
t = j
if(i and dist[t] == float("inf")):
return float("inf")
if(i):
res+=dist[t]
for j in range(100):
dist[j] = min(dist[j],g[t][j])
Kruskra 算法
这个也是,只是适用于稀疏图。
def Kruskra():
"""
定义这个数据是存储边的
:return:
"""
# 这个P的话就是Parents数组
p = [0]
res = 0
cnt = 0
Nodes = [Node() for _ in range(100)]
sorted(Nodes,lambda node:node.c)
for i in range(100):
node = Nodes[i]
a = find(node.a,p)
b = find(node.b,p)
if(a!=b):
p[a] = b
res+=node.c
cnt+=1
#此时是不连通的
if(cnt<100-1):
return float("inf")
染色法
那么之后的话,是关于我们二分图的一个东西,首先是判断是不是二分图,然后在是对二分图进行操作。
"""
0 表示没有染色,1表示白色,2表示黑色
"""
def upColor(color,a,c):
color[a] = c
i = h[a]
while(i!=-1):
j = e[i]
if(not color[j]):
if(not upColor(st,j,3-c)):
return False
elif(color[j]==c):
return False
i = ne[i]
return True
def check():
for i in range(1,n+1):
if(not upColor(st,i,1)):
return False
return True
Hunger算法
这个就是咱们的这个匈牙利算法,在我们已经确定了这个是个二分图的情况下,我们可以使用这个来进行一个匹配。
那么在这里的话,我们依然给出的是使用邻接表来做的模板,然后的话,我们这里的话有一点可以注意的就是,我们在使用这个算法的时候,因为只有左侧的是会被用到的,所以的话存储的话,存入左侧的线就可以了,当然如果需要存入右侧也是可以的,但是用不到,所有必要。
这里是左侧匹配右侧,然后左侧是n1,右侧是n2
def Match(st,match,a):
i = h[a]
while(i!=-1):
j = e[i]
if(not st[j]):
st[j] = True
if(match[j]==0 or Match(st,match,j)):
match[j] = a
return True
i = ne[i]
return False
def Hunager():
res = 0 #匹配个数
Match = [0 for _ in range(10000)] #右侧的集合元素和左侧的谁进行了匹配
for i in range(1,n1+1):
# 表示右边的那个集合元素有没有匹配到
st = [False for _ in range(10000)]
if(Match(st,match,i)):
res+=1
return res