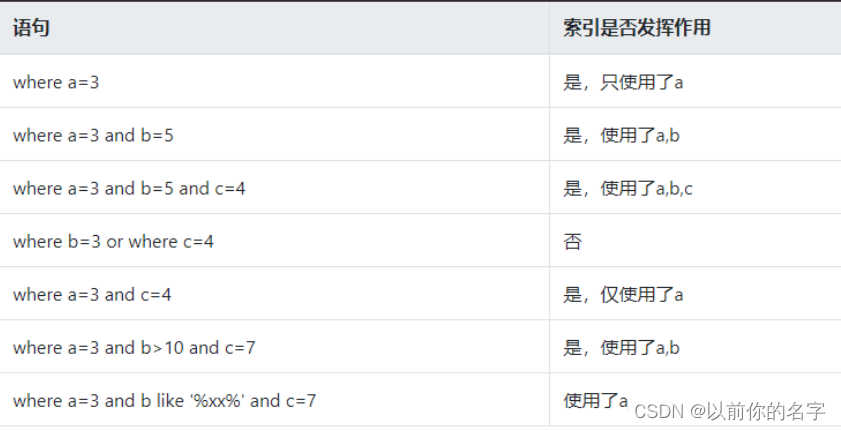
层序遍历
题目详细:LeetCode.102
层序遍历与上一节讲的三种遍历方式有所不同,层序遍历是指按从上到下,从左到右的顺序,逐层地遍历二叉树的节点。
从其节点的遍历顺序上观察,我们可以发现其跟广度优先遍历(BFS)的遍历思想非常相似,既然我们可以利用队列先进先出的特点来实现广度优先遍历,那么我们也可以用队列来实现对二叉树的层序遍历:
- 定义一个二维数组,其下标表示第i层,数组元素则存储着每一层遍历的节点
- 定义一个队列,利用其先进先出的特点,先将非空的根节点进队
- 定义一个循环,遍历入队的二叉树节点
- 定义一个变量,记录每一层的节点数目,也就是当前队列的长度
- 定义一个循环,获取变量得知在第一层,只有根节点一个节点
- 那么我们只需要出队一次,将根节点出队,队列长度 - 1
- 定义一个一维数组存放该层的节点值,并将该数组追加入到二维数组中
- 然后将其非空的左右节点依次进队
- 循环直到该层的节点都遍历完毕
- 循环直到队列为空,说明二叉树层序遍历完成
Java解法(队列,BFS):
class Solution {
public List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
this.bfs(root);
return ans;
}
public void bfs(TreeNode root){
Queue<TreeNode> queue = new LinkedList<>();
if(null != root) queue.offer(root);
while(!queue.isEmpty()){
int n = queue.size();
List<Integer> floor = new ArrayList<>();
while(n-- > 0){
TreeNode node = queue.poll();
floor.add(node.val);
if(null != node.left) queue.offer(node.left);
if(null != node.right) queue.offer(node.right);
}
ans.add(floor);
}
}
}
这道题我们可以模拟层序遍历的思想,利用递归来解题,只需要在递归函数中增加一个变量,记录节点是第几层的即可:
Java解法(模拟,递归):
class Solution {
public List<List<Integer>> ans = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
this.order(root, 0);
return ans;
}
public void order(TreeNode root, int level){
if(null == root) return;
if(level > ans.size() - 1){
List<Integer> floor = new ArrayList<>();
floor.add(root.val);
ans.add(floor);
}else{
ans.get(level).add(root.val);
}
this.order(root.left, level + 1);
this.order(root.right, level + 1);
}
}
学会了二叉树的层序遍历后,可以一口气打完以下十道LeetCode题:
102.二叉树的层序遍历
104.二叉树的最大深度
107.二叉树的层次遍历II
111.二叉树的最小深度
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针II
199.二叉树的右视图
429.N叉树的层序遍历
515.在每个树行中找最大值
637.二叉树的层平均值
翻转二叉树
题目详细:LeetCode.226
翻转二叉树的过程和结果:

观察上图动画我们可以发现,上图采用的是层序遍历的顺序,在遍历的过程中,将每个节点的左右节点进行交换,这就是翻转二叉树的解题思想。
所以想要解题很简单,就是采用合适的遍历方法,在访问节点的时候,将其左右节点进行交换即可;
需要注意的是,在这道题中我们采用的遍历二叉树方法一般是:前序遍历、后序遍历和层序遍历,因为采用中序遍历的方式会导致重复交换子节点,需要在遍历过程中加以逻辑判断才能避免这一情况,不易编写和理解。
如何遍历在这里就不作赘述了,不了解的可以查看上一节的内容,详细讲述了遍历二叉树的各种方法:【Day14】传送门
Java解题(递归,前序遍历):
class Solution {
public TreeNode invertTree(TreeNode root) {
this.invertPre(root);
return root;
}
public void swapChildNode(TreeNode node){
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
}
public void invertPre(TreeNode root){
if(null == root) return;
this.swapChildNode(root);
this.invertPre(root.left);
this.invertPre(root.right);
}
}
Java解题(统一迭代,前序遍历):
class Solution {
public TreeNode invertTree(TreeNode root) {
this.invertPre(root);
return root;
}
public void swapChildNode(TreeNode node){
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
}
public void invertPre(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
if(null != root) stack.push(root);
while(!stack.isEmpty()){
// 标记节点
TreeNode tagNode = stack.peek();
if(tagNode != null){
// 非标记节点,先弹出,在需要处理的节点后追加空指针作为标记(仅作标记,不作处理)
TreeNode node = stack.pop();
if(null != node.right) stack.push(node.right);
if(null != node.left) stack.push(node.left);
stack.push(node);
stack.push(null);
}else{
// 遇到标记节点,先弹出作为标记的空指针的节点,再处理数据(处理节点,不作标记)
stack.pop();
TreeNode node = stack.pop();
this.swapChildNode(node);
}
}
}
}
对称二叉树
题目详细:LeetCode.101
由题可知,判断一棵二叉树是否对称:
- 根节点无需比较
- 接着比较树的内侧的节点和外侧的节点,而不是比较树的左右节点
- 当每棵子树都满足内侧节点相等,外侧节点相等,那么则称这整棵二叉树是对称的
所以关键在于如何遍历二叉树,以及如何比较树的内侧节点和外侧节点。
既然根节点不需要比较,那么我们就需要同时比较其左右两棵子树上的节点,在比较过程中,会出现四种情况:
- 左右节点皆为空,则是对称的
- 左右节点只有一个为空,则是不对称的
- 左右节点皆不为空,但是他们的值不相等,是不对称的
- 左右节点皆不为空,但是他们的值相等,是对称的
所以对于每一棵子树,我们只需要按照上述情况去比较其内侧和外侧节点,就可以得到正确答案:
- 树的
内侧节点选左子树的右节点和右子树的左节点进行比较 - 树的
外侧节点选左子树的左节点和右子树的右节点进行比较 - 当出现一种不对称情况时,则整个树是不对称的,无需继续比较
- 当出现对称情况时,继续比较剩余的左右子树
Java解题(递归):
class Solution {
public boolean isSymmetric(TreeNode root) {
return this.check(root.left, root.right);
}
public boolean check(TreeNode leftNode, TreeNode rightNode){
if(null == leftNode && null == rightNode)
return true;
else if(null == leftNode || null == rightNode || leftNode.val != rightNode.val)
return false;
return check(leftNode.right, rightNode.left) && check(leftNode.left, rightNode.right);
}
}
Java解题(迭代,队列):
class Solution {
public Queue<TreeNode> queue = new LinkedList<>();
public boolean isSymmetric(TreeNode root) {
return this.check(root.left, root.right);
}
public boolean check(TreeNode leftNode, TreeNode rightNode){
this.queue.offer(leftNode);
this.queue.offer(rightNode);
while(!queue.isEmpty()){
leftNode = queue.poll();
rightNode = queue.poll();
if(null == leftNode && null == rightNode)
continue;
else if(null == leftNode || null == rightNode || leftNode.val != rightNode.val){
return false;
this.queue.offer(leftNode.right);
this.queue.offer(rightNode.left);
this.queue.offer(leftNode.left);
this.queue.offer(rightNode.right);
}
return true;
}
}
观察代码以及二叉树的遍历过程,我们也可以发现,对于对称二叉树的遍历顺序,左子树的遍历顺序是右左根,而右子树的遍历顺序是左右根,两者都属于后序遍历,也就是说,这道题是基于后序遍历来解决的。
除了在二叉树中常用的递归方法外,我们还可以结合前面学习的其他数据结构,如栈和队列,也能够辅助我们遍历和处理二叉树。
最后这两天做二叉树相关的题目之后,给我的感触就是,二叉树的题目千变万化,但是总结起来就是两个要点:选择最佳的遍历顺序 + 处理节点的需求逻辑,可见解答二叉树相关的题目时,理解和掌握二叉树不同的遍历思想是尤其重要的:
水之积也不厚,则其负大舟也无力。