作者：指针不指南吗
专栏：算法篇

🐾合理规划时间与精力🐾

1.什么是差分？

与前缀和是反函数

原数组a

a1 , a2 , a3 , a4 , a5 , a6 , a7

构造数组b

a1=b1;

a2=b1+b2;

a3=b1+b2+b3;

…

ai=b1+b2+b3+…+bi;

构造一个b数组使得，他的前缀和是 a；

则b就是a的差分。

---

2.怎么求差分？

差分b , 前缀和 a;

• 第一种

for(int i=1;i<=n;i++){
	cin>>a[i];
	b[i]=a[i]-a[i-1];
}

• 第二种 利用函数，在问题具体操作时保持一致

void insert(int l,int r,int c)
{
	b[l]+=c;
    b[r+1]-=c;
}

for(int i=1;i<=n;i++){
	cin>>a[i];
	insert(i,i,a[i]);  //原来 b中都是0，现在插上
}

---

3.差分有什么用

对一段区间 [ l , r ] 的每个数加上 c，每个数多少

差分 b[ l ] + = c ，则 a[ l ~ n ] 全部都加上 c ,因为a[l]=...+b[l] ,a[l+1]=...+b[l]+b[l+1]

但是注意 r 之后的元素也都加上 c 了，这个不是我们想要的，所以打个补丁 ，令 b[ r + 1 ] - = c ;

优点是：时间复杂度为线性的

#include<iostream>
using namespace std;

const int N=100010;
int a[N],b[N];

int n,m; //n 数组元素个数；m 表示操作次数

void insert(int l,int r,int c){
	b[l]+=c;   //对差分+c
	b[r+1]-=c;  //补丁
}

int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		insert(i,i,a[i]);  //差分b 数组
	}
	
	while(m--){
		int l,r,c;        //对差分 b 操作
		cin>>l>>r>>c;    
		insert(l,r,c);   //对区间进行元素进行操作
	}
	
	for(int i=1;i<=n;i++){    //求出原数组即前缀和a
		a[i]=a[i-1]+b[i];
		cout<<a[i]<<' ';
	}
	
	return 0;
} 

---

4.进阶： 二维差分

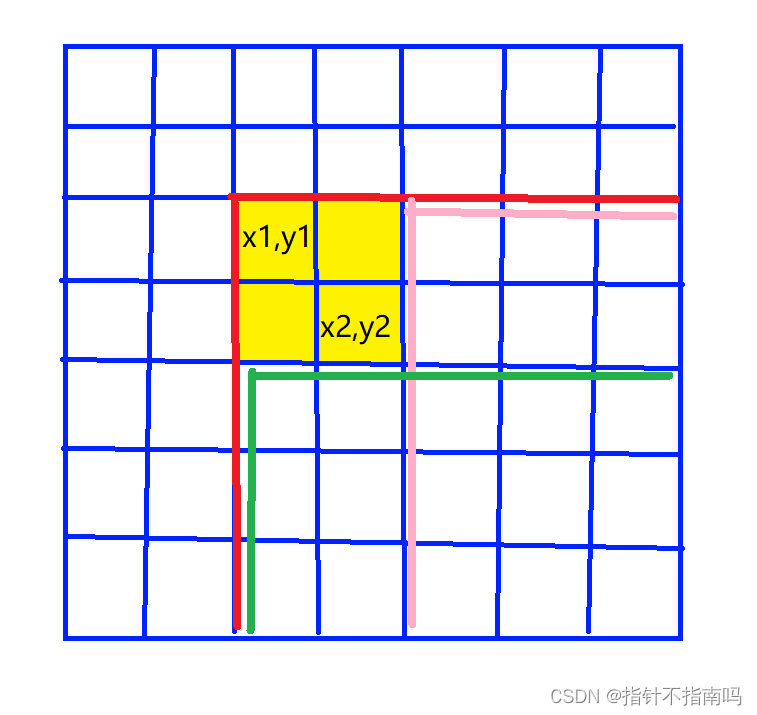
黄色部分(x1,y1),(x2,y2)内的每个数加上 c

黄色 + c = (红色顶点+c) - (绿色顶点 - c ) - ( 粉色顶点 - c ) + ( 混合 色顶点)

差分处理 ：

b [ x1 ] [ y1 ] + = c ;

b [ x1 ] [ y2 - 1 ] - = c ;

b [ x2 ] [ y1 - 1 ] - = c ;

b [ x2 - 1 ] [ y2 - 1 ] + = c ;

---

• 代码实现

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ ){
        	scanf("%d", &a[i][j]);
        	insert(i, j, i, j, a[i][j]);
		}
    
    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; i ++ ){
    	for (int j = 1; j <= m; j ++ ){
        	b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
        	printf("%d ", b[i][j]);
		}
    	puts(" ");
	}
	
	return 0;
}