入门深度学习——基于全连接神经网络的手写数字识别案例(python代码实现)
一、网络构建
1.1 问题导入
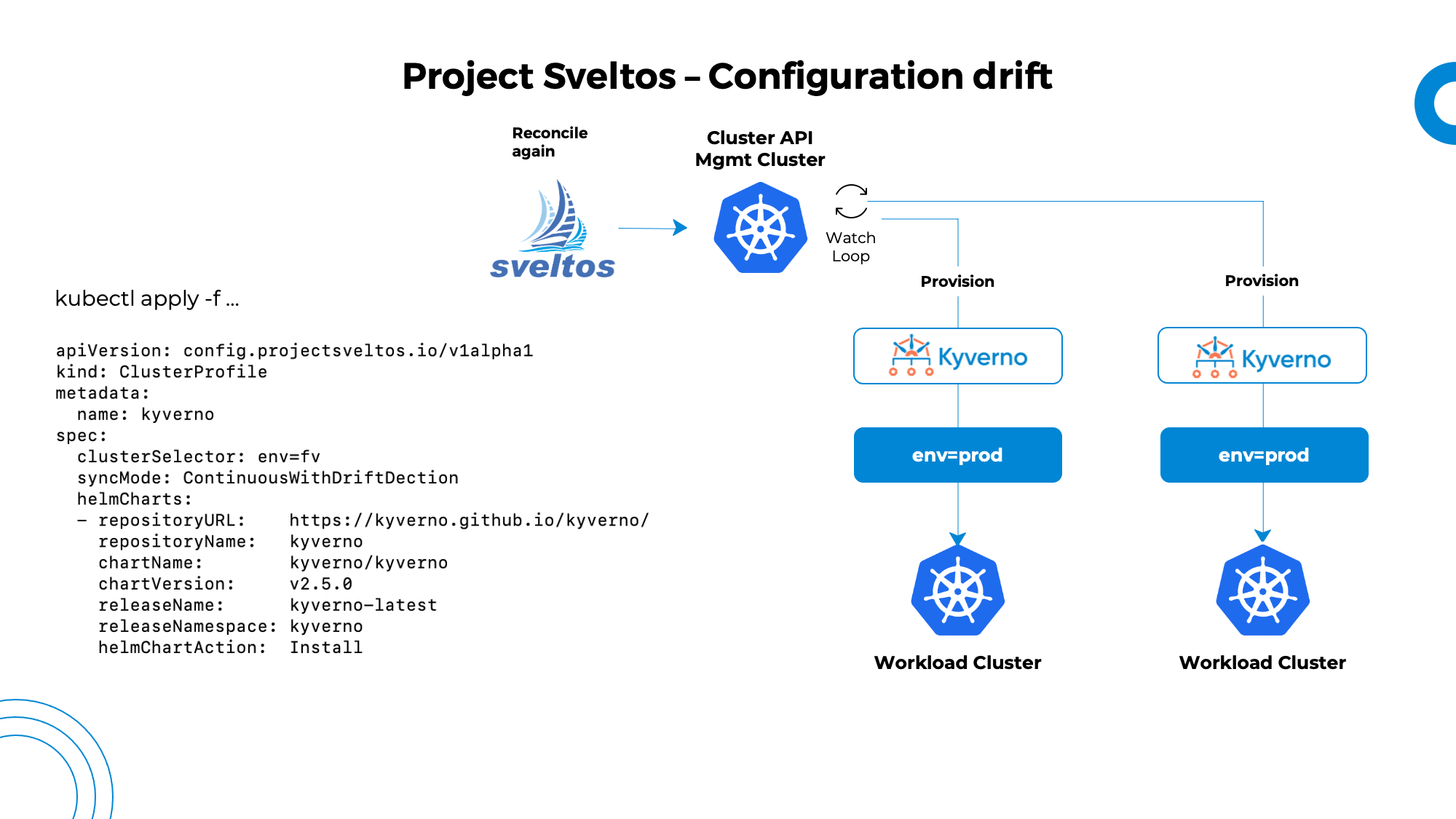
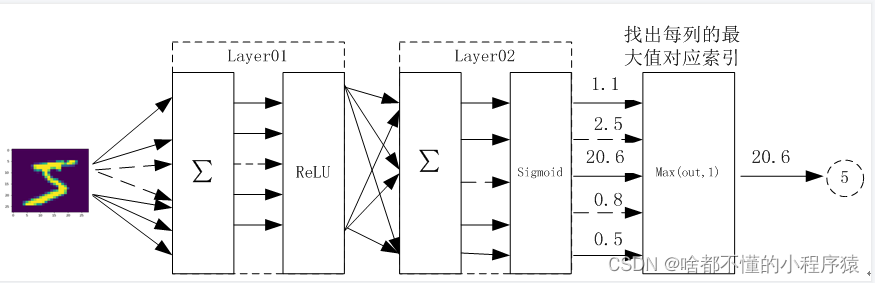
如图所示,数字五的图片作为输入,layer01层为输入层,layer02层为隐藏层,找出每列最大值对应索引为输出层。根据下图给出的网络结构搭建本案例用到的全连接神经网络
1.2 手写字数据集MINST
如图所示,MNIST数据集是机器学习领域中非常经典的一个数据集,由60000个训练样本和10000个测试样本组成,每个样本都是一张28 * 28像素的灰度手写数字图片。数据集也被嵌入到sklearn和pytorch框架中可以直接调用。这里我们默认已经安装了pytorch框架。不会使用的这里简单介绍一下。
大家可以用按住win+R键,打开运行窗口,输入cmd。

输入cmd,回车后,会显示如下。

输入以下的命令,可以看看自己的电脑的显卡是不是NVIDIA。如果是AMD的,那么就安装cpu的吧,毕竟CUDA内核,只支持NVIDIA的显卡。
#AMD显卡
pip install pytorch-cpu
#NVIDIA显卡
pip install pytorch
#如果速度慢的话,可以加入清华源的链接
pip install pytorch-cpu -i https://pypi.tuna.tsinghua.edu.cn/simple/
#NVIDIA显卡
pip install pytorch -i https://pypi.tuna.tsinghua.edu.cn/simple/
这样就完成了,仍然存在问题的小伙伴,可以参考小程序员推荐的这个up主的教程pytorch保姆级教程。
这里我们输出几张图片和对应的标签。作为对数据集的了解,也方便我们针对性的设计网络结构,做到心中有数。

二、采用Pytorch框架编写全连接神经网络代码实现手写字识别
2.1 导入必要的包
import torch
import numpy as np
from torch import nn
import torch.nn.functional as F
from torchvision import datasets,transforms
from torch.utils.data import DataLoader
2.2 定义一些数据预处理操作
pipline=transforms.Compose([transforms.ToTensor(),transforms.Normalize([0.5],[0.5])])
2.3 下载数据集(训练集vs测试集)
train_dataset=datasets.MNIST('./data',train=True,transform=pipline,download=True)
test_dataset=datasets.MNIST('./data',train=False,transform=pipline,download=True)
print(len(train_dataset))
print(len(test_dataset))
60000
10000
2.4 分批加载训练集和测试集中的数据到内存里
train_loader=DataLoader(train_dataset,batch_size=32,shuffle=True)
test_loader=DataLoader(test_dataset,batch_size=32)
2.5 可视化数据集中的数据,做到心中有数
import matplotlib.pyplot as plt
examples=enumerate(train_loader)
_,(example_data,example_label)=next(examples)
print(example_data.shape)
for i in range(6):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0],cmap='gray')
# plt.title('Ground Truth:{}'.format(example_label[i]))
plt.title(f'Ground Truth:{example_label[i]}')
torch.Size([32, 1, 28, 28])
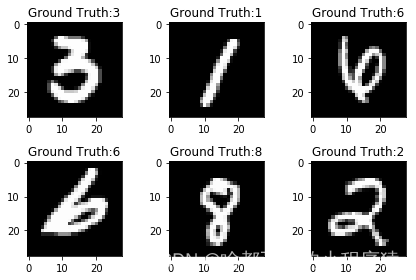
2.6 网络模型设计(有时也称为网络模型搭建)
class Net(nn.Module):
def __init__(self,in_dim,n_hidden_1,n_hidden_2,out_dim):
super(Net,self).__init__()
self.layer1=nn.Sequential(nn.Linear(in_dim,n_hidden_1),nn.ReLU(True))
self.layer2=nn.Sequential(nn.Linear(n_hidden_1,n_hidden_2),nn.Sigmoid())
self.layer3=nn.Linear(n_hidden_2,out_dim)
def forward(self,x):
x=self.layer1(x)
x=self.layer2(x)
x=self.layer3(x)
return x
model=Net(28*28,300,100,10)
model
以下结果来自Jupyter Notebook
Net(
(layer1): Sequential(
(0): Linear(in_features=784, out_features=300, bias=True)
(1): ReLU(inplace=True)
)
(layer2): Sequential(
(0): Linear(in_features=300, out_features=100, bias=True)
(1): Sigmoid()
)
(layer3): Linear(in_features=100, out_features=10, bias=True)
)
import torch.optim as optim
criterion=nn.CrossEntropyLoss() #选用Pytorch中nn模块封装好的交叉熵损失函数
optimizer=optim.SGD(model.parameters(),lr=0.01,momentum=0.5) #选用随机梯度下降法(SGD)作为本模型的梯度下降法
device=torch.device('cuda' if torch.cuda.is_available() else 'cpu') #确定代码运行设备究竟实在GPU还是CPU上跑
model.to(device)
2.7 训练网络模型
losses=[]
acces=[]
eval_losses=[]
eval_acces=[]
#训练轮数---epoch
for epoch in range(10):
train_loss=0
train_acc=0
model.train() #启用网络模型隐藏层中的dropout和BN(批归一化)操作
if epoch%5==0: #控制训练轮数间隔
optimizer.param_groups[0]['lr']*=0.9 #动态调整学习率
for img,label in train_loader:
img=img.to(device) #将训练图片写到设备里
label=label.to(device) #将图片类别写到设备里
img=img.view(img.size(0),-1)
out=model(img) #调用前向传播函数得到预测值
loss=criterion(out,label) #计算预测值和真实值的损失
optimizer.zero_grad() #在新一轮反向传播开始前,清空上一轮反向传播得到的梯度
loss.backward() #把上一部得到的损失执行反向传播,得到新的网络模型参数(权值)
optimizer.step() #把上一部得到的新的权值更新到网络模型里
#在前面前向传播和反向传播的额基础上,计算一些训练算法性能指标
train_loss+=loss.item() #记录反向传播每一轮得到的损失
_,pred=out.max(1) #得到图片的预测类别
num_correct=(pred==label).sum().item() #获取预测正确的样本数量
acc=num_correct/img.shape[0] #每一批次的正确率
train_acc+=acc #每一轮次的额正确率
losses.append(train_loss/len(train_loader)) #所有轮次训练完之后总的损失
acces.append(train_acc/len(train_loader)) #所有轮次训练完之后总的正确率
2.8 在测试集上测试网络模型,检验模型效果
eval_loss=0
eval_acc=0
model.eval() #继续沿用BN操作,但是不再使用dropout操作
with torch.no_grad():
for img,label in test_loader:
img=img.to(device)
label=label.to(device)
img=img.view(img.size(0),-1)
out=model(img)
loss=criterion(out,label)
eval_loss+=loss.item() #记录每一批次的损失
_,pred=out.max(1)
num_correct=(pred==label).sum().item()
acc=num_correct/img.shape[0] #记录每一批次的准确率
eval_acc+=acc #记录每一轮的准确率
eval_losses.append(eval_loss / len(test_loader))
eval_acces.append(eval_acc / len(test_loader))
print('epoch: {}, Train Loss: {:.4f}, Train Acc: {:.4f}, Test Loss: {:.4f}, Test Acc: {:.4f}'
.format(epoch, train_loss / len(train_loader), train_acc / len(train_loader),
eval_loss / len(test_loader), eval_acc / len(test_loader)))
epoch: 0, Train Loss: 1.1721, Train Acc: 0.6760, Test Loss: 0.4936, Test Acc: 0.8692
epoch: 1, Train Loss: 0.4093, Train Acc: 0.8866, Test Loss: 0.3368, Test Acc: 0.9020
epoch: 2, Train Loss: 0.3192, Train Acc: 0.9084, Test Loss: 0.2884, Test Acc: 0.9171
epoch: 3, Train Loss: 0.2755, Train Acc: 0.9194, Test Loss: 0.2552, Test Acc: 0.9271
epoch: 4, Train Loss: 0.2429, Train Acc: 0.9290, Test Loss: 0.2251, Test Acc: 0.9349
epoch: 5, Train Loss: 0.2160, Train Acc: 0.9367, Test Loss: 0.2001, Test Acc: 0.9405
epoch: 6, Train Loss: 0.1945, Train Acc: 0.9433, Test Loss: 0.1854, Test Acc: 0.9447
epoch: 7, Train Loss: 0.1761, Train Acc: 0.9494, Test Loss: 0.1716, Test Acc: 0.9504
epoch: 8, Train Loss: 0.1601, Train Acc: 0.9540, Test Loss: 0.1597, Test Acc: 0.9527
epoch: 9, Train Loss: 0.1468, Train Acc: 0.9572, Test Loss: 0.1434, Test Acc: 0.9567
2.10可视化训练及测试的损失值
plt.title('Train Loss')
plt.plot(np.arange(len(losses)),losses);
plt.legend(['Train Loss'],loc='upper right')
损失函数的结果:

三、代码文件
小程序员将代码文件和相关素材整理到了百度网盘里,因为文件大小基本不大,大家也不用担心限速问题。后期小程序员有能力的话,将在gitee或者github上上传相关素材。
链接:https://pan.baidu.com/s/1Ce14ZQYEYWJxhpNEP1ERhg?pwd=7mvf
提取码:7mvf