D2-贪心算法-训练专题
- 贪心算法使用总结
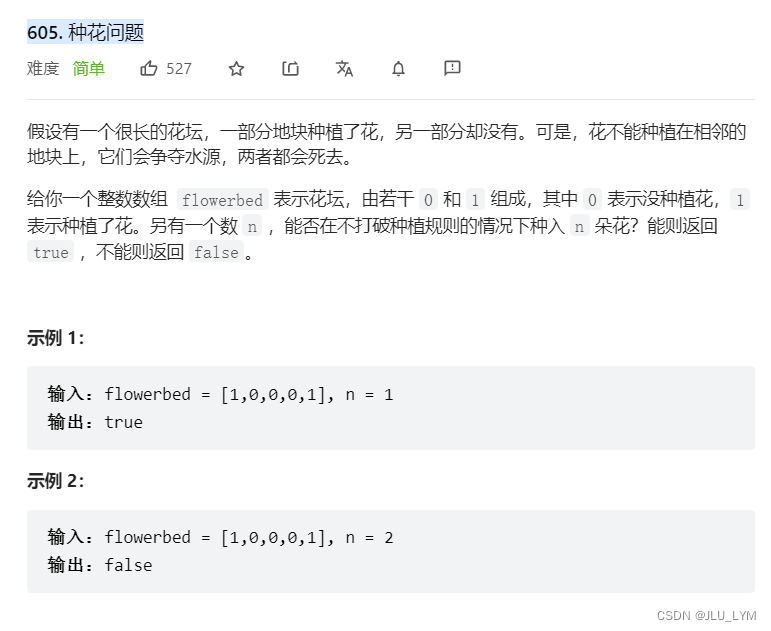
- 力扣605. 种花问题
- 思路
- 代码
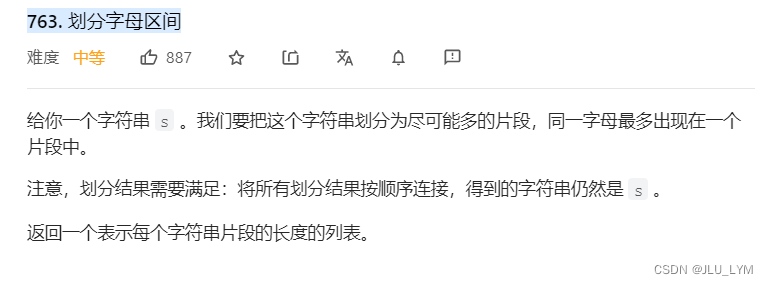
- 力扣763. 划分字母区间
- 思路
- 代码
- 另一种思路
贪心算法使用总结
当我们意识到,满足贪心算法三要素时候,解决贪心算法问题的时候,一定要遵循的步骤:
1、读懂题目限制条件
2、明确贪心算法使用的三大原则
3、切记,对原始数组中的数据,可以先进行预处理(统计一遍信息-如频率、个数、第一次出现位置、最后一次出现位置等,或者进行相关运算-如计算前缀和等)之后,再进行操作
4、制定贪心策略
力扣605. 种花问题
题目链接:605. 种花问题
思路
题目要求我们,在不打破规则的前提下,看能否种下n个东西:所以我们只需要看这个地方,最多能种多少即可,明显贪心思想。
1、一定要搞明白规则!想种东西,位置i必须满足:
1、必须是’0’
2、前后必须都得是’0’(边界也可以)
2、所以在这个规则之下,遍历一遍数组即可,发现可以种下,就把数组第i处改为1即可,统计最多可以种多少。
代码
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
int size = flowerbed.size();
int i = 0;
int cnt = 0;
while (i < size) {
if (flowerbed[i] == 1) {
i++;
}
else {
if ((i - 1 < 0 || flowerbed[i - 1] != 1) && (i + 1 >= size || flowerbed[i + 1] != 1)) {//先考虑边界,在考虑是不是0
cnt++;
flowerbed[i] = 1;
i++;
}
else {
i++;
}
}
}
return cnt >= n;
}
};
力扣763. 划分字母区间
题目链接:763. 划分字母区间

思路
根据题意,我们需要按照一定的规则进行分划数组
1、但是,我们什么额外的信息都没有,不方便操作,所以,一定要记住!!!!!!对于给出的一大串数据无头绪,先进行"预处理"工作,预处理方向有限,可以帮助我们找到数据规律,确定解题方案。
1、统计形式的预处理,包括:频率、个数、第一次出现位置、最后一次出现位置等
2、运算形式的预处理,包括:前缀和等
2、根据规则,划分好的一个片段中出现的字母,不能在其他片段中出现,所以对于任何一个字母而言,他最后一次出现的地方才可能是作为划分终点的,要不就一定违背了规则。
3、所以,预处理时候,我们存一下所有字母最后出现位置。
4、初始化划分起点终点,初始都为0。
5、用指针i遍历s,每走到一个地方,那个字母一定包括在这个片段之中,那么最终分划的位置和这个字母最后出现的位置二者取最大的,保证这个字母能完全出现在这个片段之中,当足迹i==分划终点,则这个片段分完了,这就是贪心策略
代码
class Solution {
public:
vector<int> partitionLabels(string s) {//另一种贪心思想,效率更优秀
int ends[30];
int n = s.size();
vector<int> ans;
for (int i = 0; i < n; i++) {//记录每个字母最后出现位置
ends[s[i] - 'a'] = i;
}
int b = 0, e = 0;
for (int i = 0; i < n; i++) {
e = max(e, ends[s[i] - 'a']);
if (i == e) {
ans.push_back(e - b + 1);
b = e + 1;//重新初始化下一个片段起点
}
}
return ans;
}
};
另一种思路
1、预处理中,我们可以同时收集,“刚出现位置"和"最后出现位置”,这样,任意一个字母,就都可以看成出现在一个区间上,统计出所有这些区间。
2、比如说,题目中,第一个样例,前九个元素,分成第一个片段,a出现在[0,8],b出现在[1,5],c出现在[4,7],同理再找到第二个片段中,字母出现的区间
3、不难发现:
<1>当我们列出所有的出现了的字母的区间之后,每一个片段里的字母对应的区间都是可以合并的,a、b、c有交集,可以合并成一个大的区间,恰好是[0,8]长度为9
<2>不同片段对应的字母区间,无交集,不能合并重叠区间
4、综上,这道题统计完字母出现区间之后,就转化成了合并重叠区间问题,这个详见D2-贪心算法-区间问题中的第三题
class Solution {
public:
vector<int> partitionLabels(string s) {
vector<vector<int>> section;//统计出现的字母的起始位置和终止位置
int start[30] = {};
int ends[30] = {};
vector<int> ans;
vector<bool> v(30, false);
int n = s.size();
for (int i = 0; i < n; i++) {
if (!v[s[i] - 'a']) {
start[s[i] - 'a'] = i;
v[s[i] - 'a'] = true;
}
}
for (int i = 0; i < n; i++) {
ends[s[i] - 'a'] = i;
}
for (int i = 0; i < 30; i++) {
if (v[i]) {
section.push_back({ start[i],ends[i] });
}
}
int size = section.size();
sort(section.begin(), section.end(), [](const auto& a, const auto& b) {//合并重叠区间
return a[0] < b[0];
});
int b = section[0][0], e = section[0][1];
for (int i = 1; i < size; i++) {
if (section[i][0] > e) {//不可以合并
ans.push_back(e - b + 1);//写入答案
b = section[i][0];//初始化端点位置
e = section[i][1];
}
else {//可以合并,更新端点位置
b = min(b, section[i][0]);
e = max(e, section[i][1]);
}
}
ans.push_back(e - b + 1);
return ans;
}
};