常见哈希函数

1. 直接定址法--(常用)

这种方法不存在哈希冲突
取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B
优点：简单、均匀
缺点：需要事先知道关键字的分布情况
使用场景：适合查找比较小且连续的情况
面试题：字符串中第一个只出现一次字符

只出现一次的字符串

2. 除留余数法--(常用)

存在哈希冲突，重点解决哈希冲突
设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，
按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址

3. 平方取中法--(了解)
假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；
再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址
平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况

4. 折叠法--(了解)
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这
几部分叠加求和，并按散列表表长，取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况

5. 随机数法--(了解)
选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中
random为随机数函数。
通常应用于关键字长度不等时采用此法

6. 数学分析法--(了解)
设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各位上出现的频率不一定
相同，可能在某些位上分布比较均匀，每种符号出现的机会均等，在某些位上分布不均匀只
有某几种符号经常出现。可根据散列表的大小，选择其中各种符号分布均匀的若干位作为散
列地址。

位图

面试题
给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在
这40亿个数中。【腾讯】

这里用搜索树和哈希表都不行，搜索树还有left，right，colour有额外空间，哈希表有next指针消耗，这俩种方式都会消耗空间导致内存中存不下

排序+二分查找同样数据太大，只能放在磁盘上，磁盘上不好支持二分查找
1. 遍历，时间复杂度O(N)
2. 排序(O(NlogN))，利用二分查找: logN
3. 位图解决
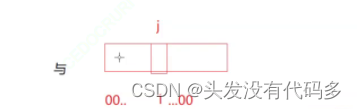
数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一
个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0
代表不存在。比如：

所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用
来判断某个数据存不存在的。

用位图的方式，这里大概占用512MB

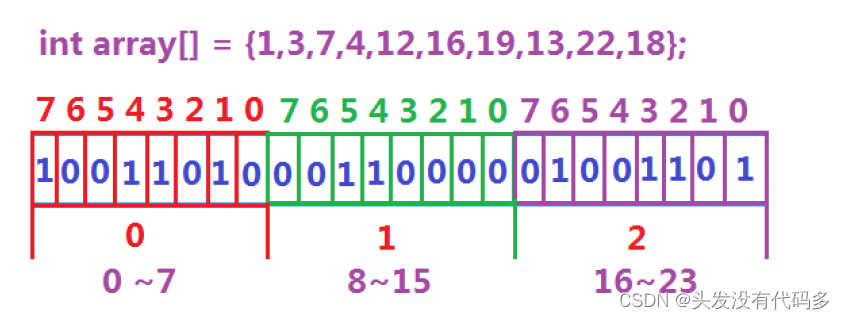
按位开空间不好开，我们按char开空间，一个char占一个字节，一个字节是8个比特位

标记为1的方法，把1进行左移或右移，之后进行按位或

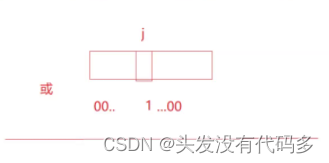
reset和set相反，reset//计算出来位置后，把那个位置标记为0，其它位标记为1

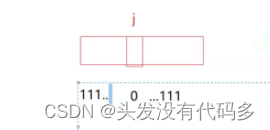
test：判断x在不在，这一位和1相与判断在不在


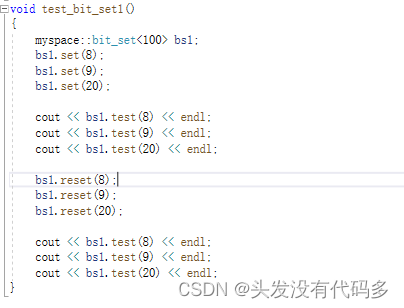
	template<size_t N>//N个比特位,
	class bitset
	{
	public:
		bitset()
			:
		{
			_bits.resize(N / 8+1, 0);//如果N对8能整除就N/8，不能对8整除就+1多开一个字节，这种浪费比较少可忽略
             
		}
		void set(size_t x)//计算在第几个char的第几个位，如20，20/8=2在第二个char，20%8=4第四个比特位
		{
			size_t i = x / 8;
			size_t j = x % 8;
			//计算出来位置后，把那个位置标记为1
			_bits[i] |= (1 << j);
		}
		void reset(size_t x)//让这位变为0，其它位是1
		{
			size_t i = x / 8;
			size_t j = x % 8;
			//计算出来位置后，把那个位置标记为0，其它位标记为1
			_bits[i] &= ~(1 << j);
		}
		bool test(size_t x)//判断x在不在
		{
			size_t i = x / 8;
			size_t j = x % 8;
			return _bits[i] & (1 << j);
		}
	private:
		vector<char> _bits;
	};

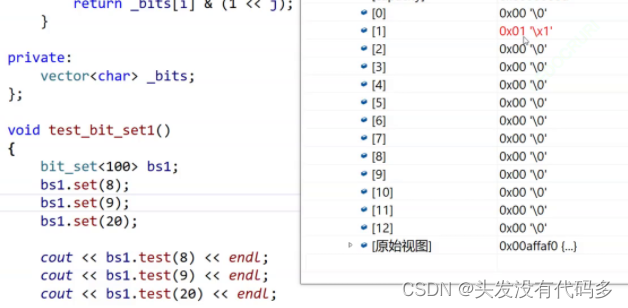
走到8的时候，第二个char显示16进制的1，说明8是第二个char的第一个比特位，是全体的第8个比特位

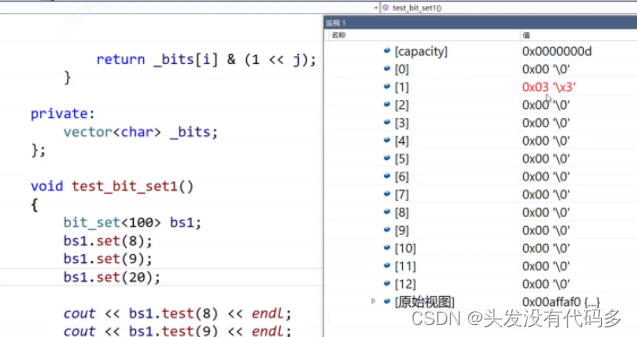
第9位是3，说明是第二个char的第二个比特位，因为要和前面8所表示的1加起来

上面40亿的数据进行位图计算，此时会溢出，-1是无符号的-1

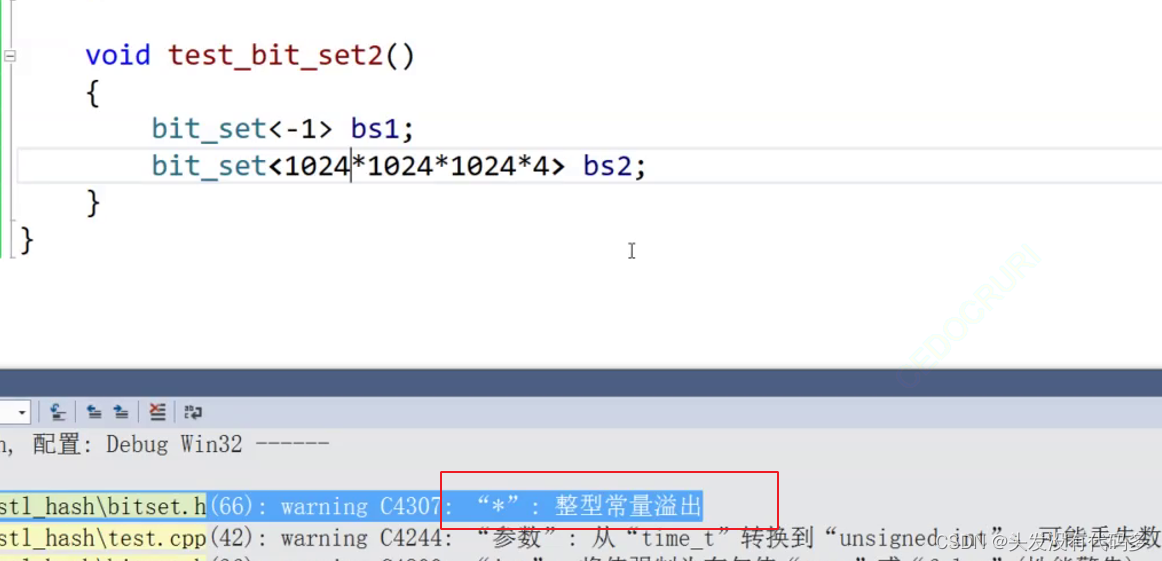
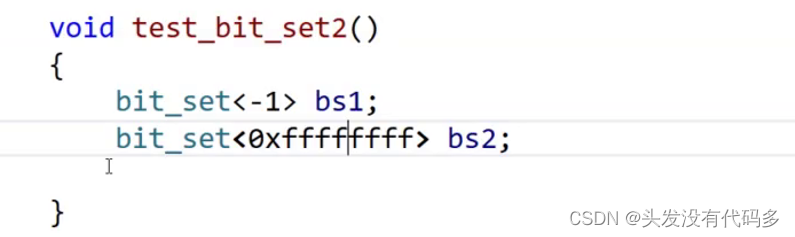
改为这种写法就不会报错，大概占用是512MB

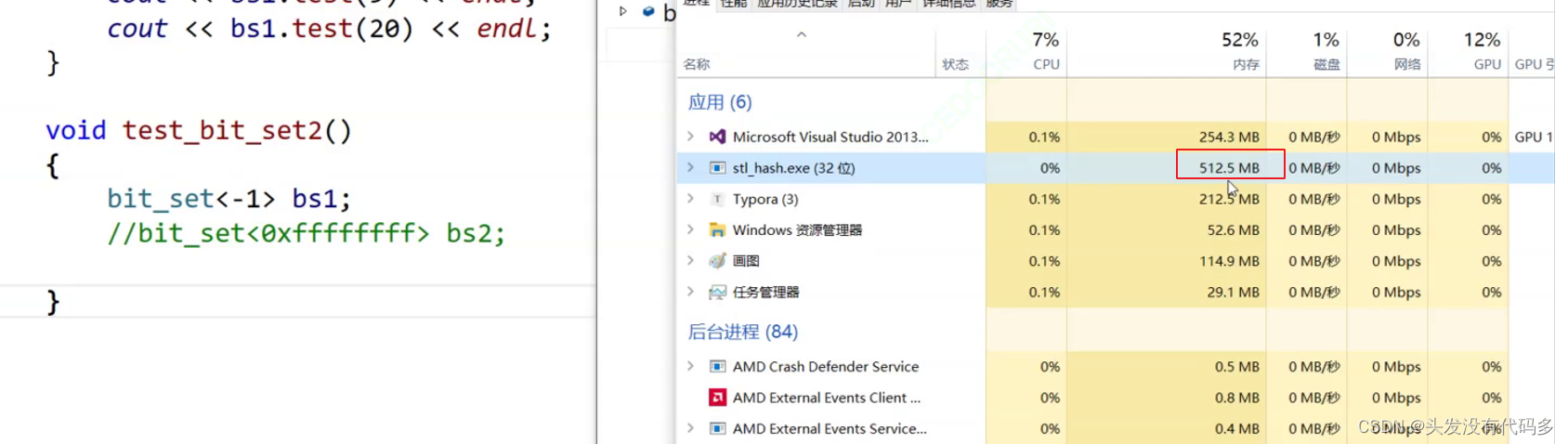
当执行完之后，内存被释放，这是因为这里是vector有自己的析构，不需要我们写

位图扩展题

1. 给定100亿个整数，设计算法找到只出现一次的整数？

kv的统计次数搜索模型，我们使用位图，俩个比特位表示一个值，大概需要一个G

我们依靠上面的代码，搞俩个位图，俩个位图相对应的位置表示一个值出现次数

	template<size_t N>//N个比特位,
	class bitset
	{
	public:
		bitset()
			:
		{
			_bits.resize(N / 8+1, 0);//如果N对8能整除就N/8，不能对8整除就+1多开一个字节，这种浪费比较少可忽略
             
		}
		void set(size_t x)//计算在第几个char的第几个位，如20，20/8=2在第二个char，20%8=4第四个比特位
		{
			size_t i = x / 8;
			size_t j = x % 8;
			//计算出来位置后，把那个位置标记为1
			_bits[i] |= (1 << j);
		}
		void reset(size_t x)//让这位变为0，其它位是1
		{
			size_t i = x / 8;
			size_t j = x % 8;
			//计算出来位置后，把那个位置标记为0，其它位标记为1
			_bits[i] &= ~(1 << j);
		}
		bool test(size_t x)//判断x在不在
		{
			size_t i = x / 8;
			size_t j = x % 8;
			return _bits[i] & (1 << j);
		}
	private:
		vector<char> _bits;
	};
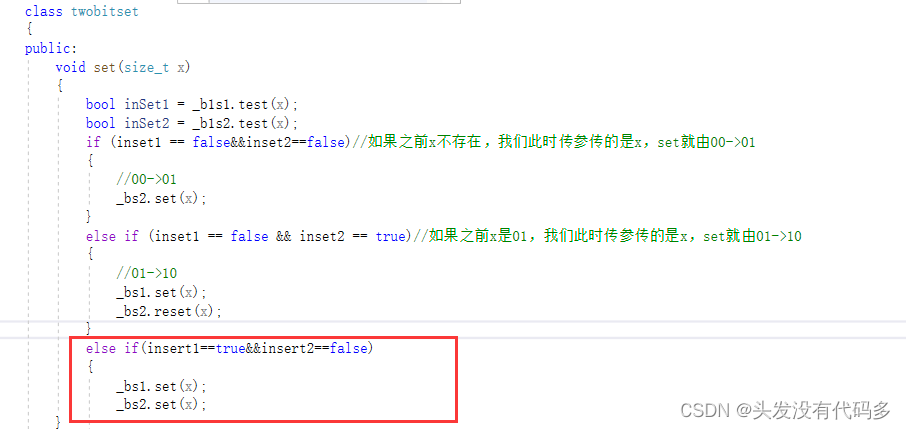
	template<size_t N>
	class twobitset
	{
	public:
		void set(size_t x)
		{
			bool inSet1 = _b1s1.test(x);
			bool inSet2 = _b1s2.test(x);
			if (inset1 == false&&inset2==false)//如果之前x不存在，我们此时传参传的是x，set就由00->01
			{
				//00->01
				_bs2.set(x);
			}
			else if (inset1 == false && inset2 == true)//如果之前x是01，我们此时传参传的是x，set就由01->10
			{
				//01->10
				_bs1.set(x);
				_bs2.reset(x);
			}
			//如果之前x是10，我们就不用管了
		}
	private:
		bitset<N> _bs1;
		bitset<N> _bs2;
	};
}

测序程序，这里只打印了出现一次的数据。

void test_bit_set3()
{
	int a[] = { 3, 4, 5, 2, 3, 4, 4, 4, 4, 12, 77, 65, 44, 4, 44, 99, 33, 33, 33, 6, 5, 34, 12 };

	myspace::twobitset<100> bs;
	for (auto e : a)
	{
		bs.set(e);
	}

	bs.print_once_num();
}
}

给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

找交集，使用俩个位图，第一个集合对应第一个位图，第二个集合对应第二个位图，如果既在位图1又在位图2，则是交集，或者俩个位图进行与，映射位都是1的就是交集
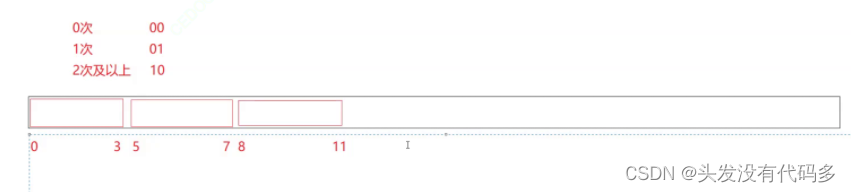
位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

这里需要四种状态00（0次），01（1次），10（2次），11（3次及以上）

位图缺点：只能处理整数
位图的优点：快，节省空间