一、递归
本章介绍程序设计中的另一个非常重要的思想一递归策略。递归是指函数直接或间接调用自身的一种方法,它通常可把一个复杂的大型问题层层转化为与原问题相似但规模较小的问题来求解。递归策略只需少量的程序就可描述解题过程所需的多次重复计算,因此大大减少了程序的代码量。
1、n的阶乘–清华大学
描述
输入一个整数n,输出n的阶乘(每组测试用例可能包含多组数据,请注意处理)
输入描述:
一个整数n(1<=n<=20)
输出描述:
n的阶乘
示例1
输入:
3
输出:
6
题解:
递归的两个关键点:
1. 递归出口
2. 递归调用
#include <iostream>
#include <cstdio>
using namespace std;
/**
* 求num的阶乘
* 注意阶乘的结果很大,所以返回值类型要是long
* @param num
* @return
*/
long factorial(int num) {
if (num == 0 || num == 1) {
/*
* 特殊值
* 0和1的阶乘都是1
*/
return 1;
}
return num * factorial(num - 1);
}
/**
* n的阶乘--清华大学
* @return
*/
int main() {
int n;
while (cin >> n) {
cout << factorial(n) << endl;
}
return 0;
}
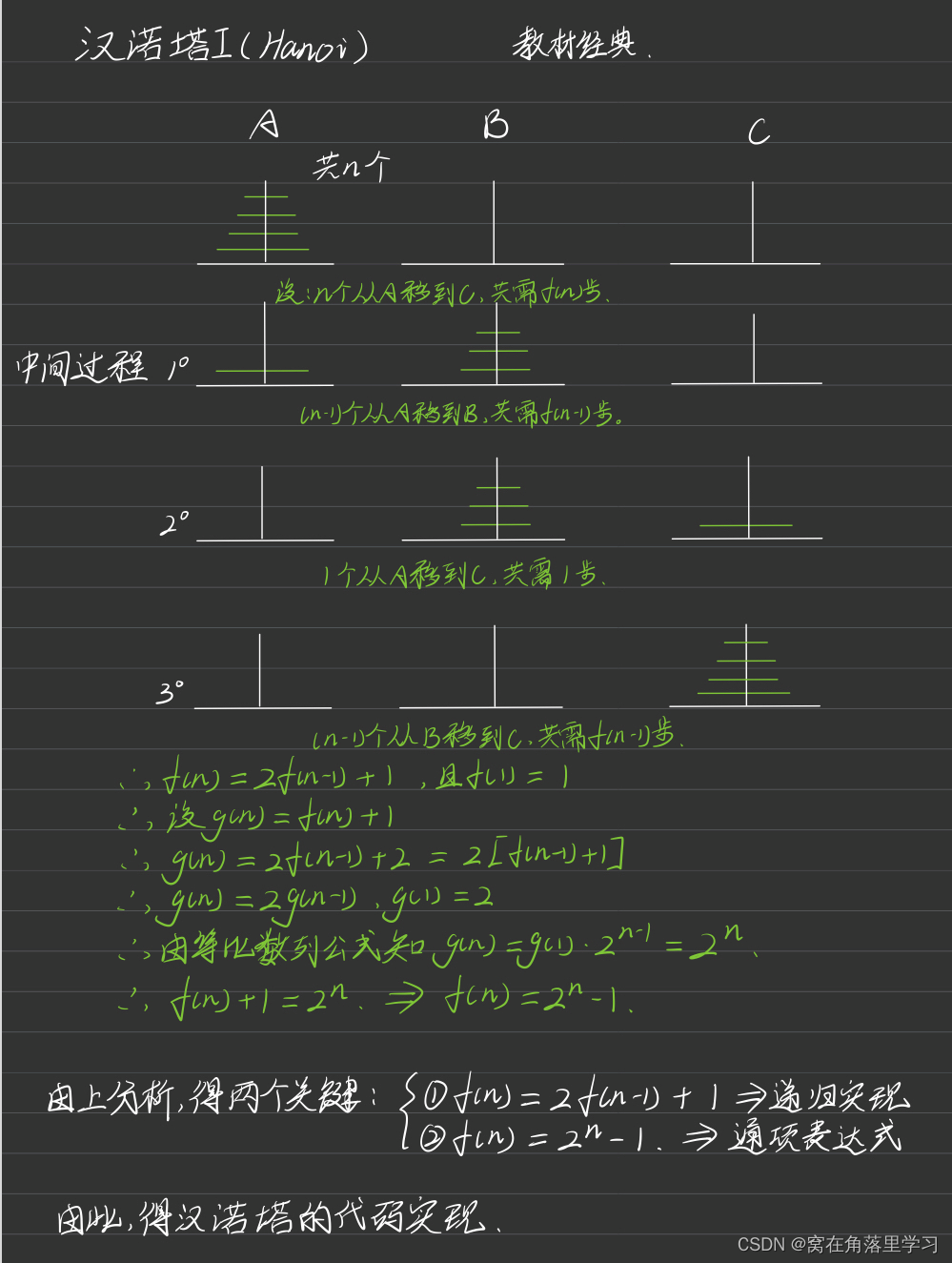
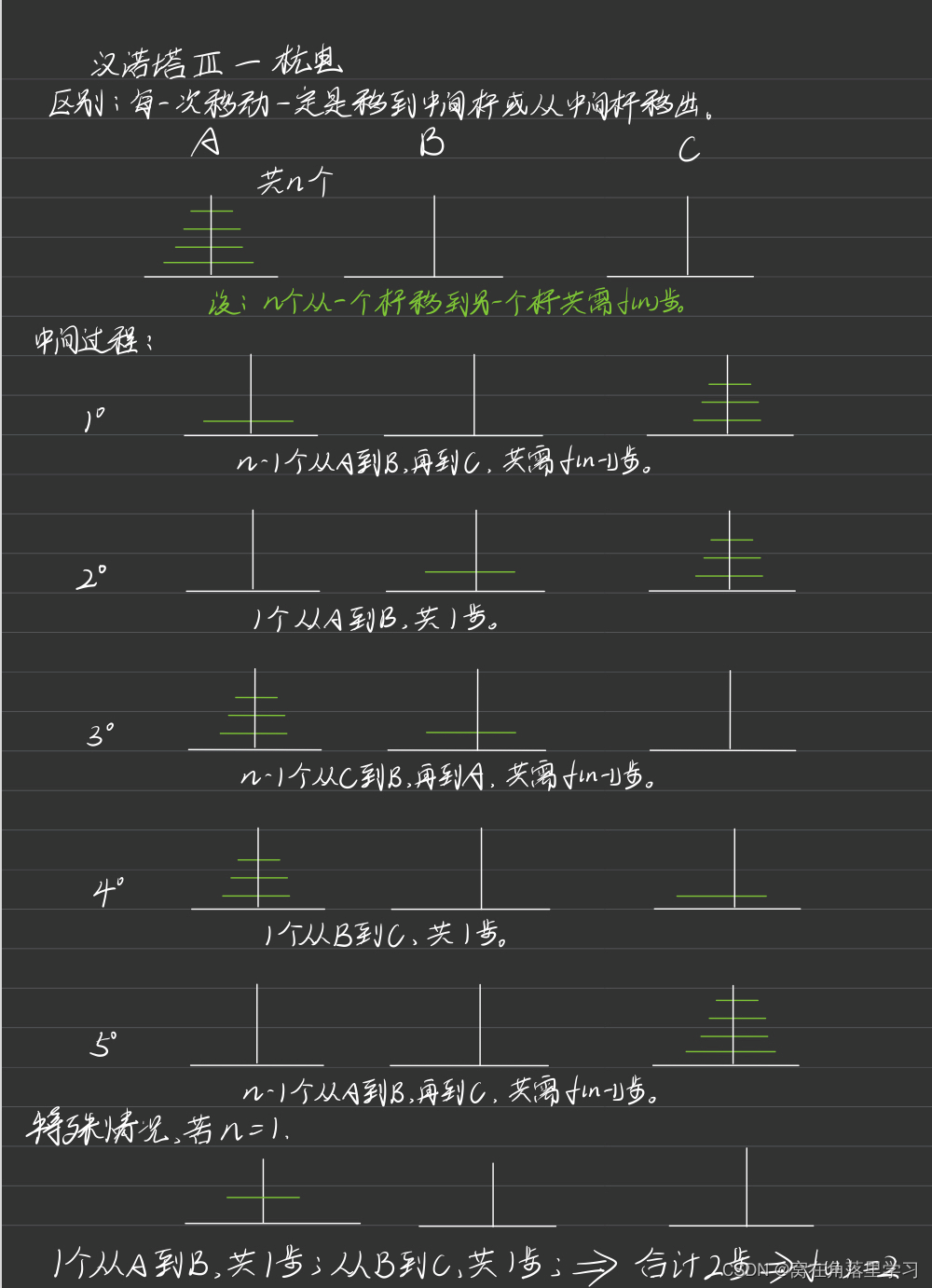
2、汉诺塔III–杭州电子科技大学
描述
约19世纪末,在欧洲的商店中出售一种智力玩具:在一块铜板上有三根杆,最左边的杆自上而
下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的圆盘全部移到右边的杆上,条件是一次只能移动一个圆盘,并且不允许大圆盘放在小圆盘的上面。现在我们改变这个游戏的玩法:不允许直接从最左(右)边移动到最右(左)边(每次移动一定是移到中间杆或从中间杆移出),也不允许大圆盘放到小圆盘的上面。Daisy已经做过原来的汉诺塔问题和汉诺塔Ⅱ问题,但碰到这个问题时,她想了很久都无法解决。请你帮助她。现在有N个圆盘,她至少需要多少次移动才能把这些圆盘从最左边移到最右边?
输入描述:
包含多组数据,每次输入一个N值(1 <= N <= 35)。
输出描述:
对于每组数据,输出移动最小的次数。
示例1
输入:
1
3
12
输出:
2
26
531440
题解:


#include <iostream>
#include <cstdio>
using namespace std;
long long Hanoi01(int n) {
if (n == 1) {
return 2;
} else {
return 3 * Hanoi01(n - 1) + 2;
}
}
long long Hanoi02(int n) {
long long ans = 1;
for (int i = 0; i < n; ++i) {
ans *= 3;
}
ans -= 1;
return ans;
}
/**
* 汉诺塔III--杭州电子科技大学
* @return
*/
int main() {
int n;
while (cin >> n) {
cout << Hanoi01(n) << endl;
//cout << Hanoi02(n) << endl;
}
return 0;
}
二、分治
分治法(Divide and Conquer)是另一个非常重要的算法。
分治法字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多个子问题,子问题之间互相独立且与原问题相同或相似。之后再把子问题分成更小的子问题,以此类推,直到最后的子问题可以简单地直接求解,原问题的解即子问题的解的合并。
由于分治法产生的子问题往往与原问题相同且模式更小,这就为使用递归策略求解提供了条件。
在这种情况下,通过反复利用分治手段,可以使子问题的规模不断缩小,最终缩小到可以直接求解的情况。在从过程中会导致了递归过程的产生。分治与递归就像一对孪生兄,经常同时应用在算法设计中,这也是将分治法和递归策略放在同一章中进行讲解的原因。
分治法的步骤如下:
1. 分:将问题分解为规模更小的子问题。
2. 治:将这些规模更小的子问题逐个击破。
3. 合:将已解决的子问题合并,最终得出"母"问题的解。
分治法 和 贪心策略
相同点:问题分解
区别:
1. 分治法--子问题可能会继续分解
2. 贪心策略--子问题将无需继续分解
1、Fibonacci–上海交通大学
描述
The Fibonacci Numbers{0,1,1,2,3,5,8,13,21,34,55…} are defined by the recurrence: F0=0 F1=1 Fn=Fn-1+Fn-2,n>=2 Write a program to calculate the Fibonacci Numbers.
输入描述:
Each case contains a number n and you are expected to calculate Fn.(0<=n<=30) 。
输出描述:
For each case, print a number Fn on a separate line,which means the nth Fibonacci Number.
示例1
输入:
1
输出:
1
题解:
三种解法:
1. 分治法--O(2ⁿ)
2. 递推法--O(n)
3. 矩阵快速幂--O(logn)
分治法
分为 F(n-1) 和 F(n-2)
将规模为N的问题分解为两个规模分别为N-1、N-2的子问题,不断分解,直到问题规模小于0或者1,便可直接得到子问题的答案。
之后将子问题的答案相加,便可得到母问题的答案。
虽然分治法不是此题的最优解法,但其思想还是值得学习的。
#include <iostream>
#include <cstdio>
using namespace std;
int fibonacci(int n) {
if (n == 1 || n == 0) {
return n;
} else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
/**
* Fibonacci--上海交通大学
* @return
*/
int main() {
int n;
while (cin >> n) {
cout << fibonacci(n) << endl;
}
return 0;
}
/*
* 递推法
*/
#include <iostream>
#include <cstdio>
using namespace std;
const int MAX = 35;
int fibonacci[MAX];
void init() {
fibonacci[0] = 0;
fibonacci[1] = 1;
/*
* 从索引2开始
*/
for (int i = 2; i < MAX; ++i) {
fibonacci[i] = fibonacci[i - 1] + fibonacci[i - 2];
}
}
/**
* Fibonacci--上海交通大学
* @return
*/
int main() {
init();
int n;
while (cin >> n) {
cout << fibonacci[n] << endl;
}
return 0;
}

/*
* 矩阵快速幂
*/
#include <iostream>
#include <cstdio>
using namespace std;
/**
* 矩阵维数
*/
const int DIMENSION = 2;
/**
* 矩阵
*/
struct Matrix {
int row;
int col;
int matrix[DIMENSION][DIMENSION];
Matrix(int row, int col) {
this->row = row;
this->col = col;
}
};
/**
* 矩阵乘法
* @param x
* @param y
* @return
*/
Matrix multiply(Matrix x, Matrix y);
/**
* 矩阵求幂
* @param x
* @return
*/
Matrix quickPower(Matrix x, int n);
/**
* 打印矩阵
* @param x
*/
void printMatrix(Matrix x);
/**
* Fibonacci--上海交通大学
* @return
*/
int main() {
int n;
while (cin >> n) {
Matrix fibonacci = Matrix(2, 2);
fibonacci.matrix[0][0] = 1;
fibonacci.matrix[0][1] = 1;
fibonacci.matrix[1][0] = 1;
fibonacci.matrix[1][1] = 0;
Matrix power = quickPower(fibonacci, n);
Matrix tmp = Matrix(2, 1);
tmp.matrix[0][0] = 1;
tmp.matrix[1][0] = 0;
Matrix ans = multiply(power, tmp);
/*
* 可以打印矩阵进行验证
*/
//printMatrix(ans);
cout << ans.matrix[1][0] << endl;
}
return 0;
}
Matrix multiply(Matrix x, Matrix y) {
Matrix ans(x.row, y.col);
for (int i = 0; i < ans.row; ++i) {
for (int j = 0; j < ans.col; ++j) {
ans.matrix[i][j] = 0;
for (int k = 0; k < x.col; ++k) {
ans.matrix[i][j] += x.matrix[i][k] * y.matrix[k][j];
}
}
}
return ans;
}
Matrix quickPower(Matrix x, int n) {
Matrix ans = Matrix(x.row, x.col);
for (int i = 0; i < ans.row; ++i) {
for (int j = 0; j < ans.col; ++j) {
if (i == j) {
ans.matrix[i][j] = 1;
} else {
ans.matrix[i][j] = 0;
}
}
}
while (n != 0) {
if (n % 2 == 1) {
ans = multiply(ans, x);
}
n = n >> 1;
x = multiply(x, x);
}
return ans;
}
void printMatrix(Matrix x) {
for (int i = 0; i < x.row; ++i) {
for (int j = 0; j < x.col; ++j) {
if (j == 0) {
cout << x.matrix[i][j];
} else {
cout << " " << x.matrix[i][j];
}
}
cout << endl;
}
}
2、二叉树–北京大学
描述
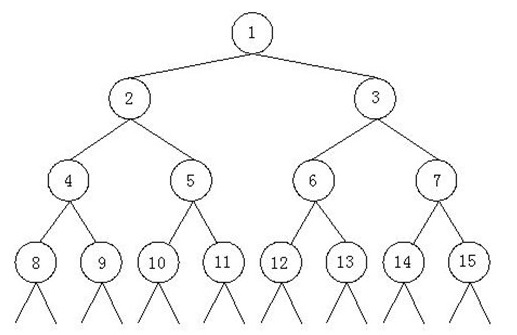
如上所示,由正整数1,2,3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是,结点m所在的子树中一共包括多少个结点。 比如,n = 12,m = 3那么上图中的结点13,14,15以及后面的结点都是不存在的,结点m所在子树中包括的结点有3,6,7,12,因此结点m的所在子树中共有4个结点。
输入描述:
输入数据包括多行,每行给出一组测试数据,包括两个整数m,n (1 <= m <= n <= 1000000000)。
输出描述:
对于每一组测试数据,输出一行,该行包含一个整数,给出结点m所在子树中包括的结点的数目。
示例1
输入:
3 12
0 0
输出:
4
题解:
对于求根结点为m的树中有多少结点数目这个问题,可以将问题分解为求它左子树和右子树的结点数目这两个相同的子问题。
在得到其左、右子树的结点数目后,加上结点m本身便可得到问题的解。
当结点m大于时,以m为根结点的树为空,那么该树的结点数目必定为0,这个便是这个问题可被轻松求解的底层子问题,也是递归出口。
#include <iostream>
#include <cstdio>
using namespace std;
int countNode(int m, int n) {
if (m > n) {
/*
* 递归出口
* 因为一共就n个顶点,所以m>n时结束即可
*/
return 0;
} else {
/*
* 根节点+左子树的节点数+右子树的节点数
*/
return 1 + countNode(2 * m, n) + countNode(2 * m + 1, n);
}
}
/**
* 二叉树--北京大学
* @return
*/
int main() {
int m;
int n;
while (cin >> m >> n) {
cout << countNode(m, n) << endl;
}
return 0;
}