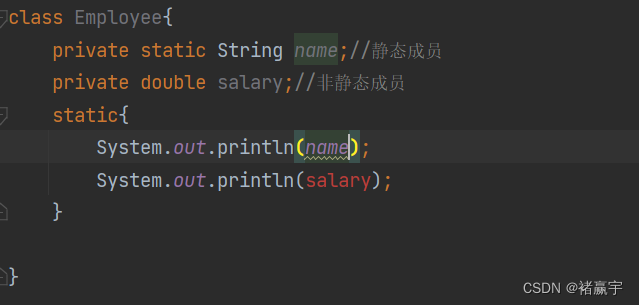
描述

给定一个 n 行 m 列矩阵 matrix ，矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径，使这条路径上的元素是递增的。并输出这条最长路径的长度。

这个路径必须满足以下条件：

1. 对于每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外。

2. 你不能走重复的单元格。即每个格子最多只能走一次。

 

int nextp[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
class Solution {
public:
    int res = 0;
    vector<int> temp;
    void dfs(vector<vector<int>>& matrix, vector<vector<bool>>& book, int curX, int curY, int row, int col)
    {
        book[curX][curY] = true;
        temp.push_back(matrix[curX][curY]);
        if(res < temp.size())
            res = temp.size();
        for(int i = 0; i < 4; i++)
        {
            int newX = curX + nextp[i][0];
            int newY = curY + nextp[i][1];
            if(newX<0 || newX>=row
            || newY<0 || newY>=col)
                continue;
            if(book[newX][newY]==false && matrix[newX][newY]>matrix[curX][curY])
            {
                dfs(matrix, book, newX, newY, row, col);
            }
        }
        book[curX][curY] = false;
        temp.pop_back();
    }
    int solve(vector<vector<int> >& matrix) {
        // write code here
        int row = matrix.size();
        int col = matrix[0].size();
        vector<vector<bool>> book(row, vector(col, false));
        for(int i = 0; i < row; i++)
        {
            for(int j = 0; j < col; j++)
            {
                dfs(matrix, book, i, j, row, col);
            }
        }
        return res;
    }
};

数据范围：1≤n,m≤10001≤n,m≤1000，0≤matrix[i][j]≤10000≤matrix[i][j]≤1000

进阶：空间复杂度 O(nm)O(nm) ，时间复杂度 O(nm)O(nm)

例如：当输入为[[1,2,3],[4,5,6],[7,8,9]]时，对应的输出为5，

其中的一条最长递增路径如下图所示：

示例1

输入：

[[1,2,3],[4,5,6],[7,8,9]]

返回值：

5

说明：

1->2->3->6->9即可。当然这种递增路径不是唯一的。       

示例2

输入：

[[1,2],[4,3]]

返回值：

4

说明：

 1->2->3->4   

备注：

矩阵的长和宽均不大于1000，矩阵内每个数不大于1000