目录
1.二叉搜索树
1.1 二叉搜索树概念
1.2 二叉搜索树操作
1.3 二叉搜索树的实现
1.4 二叉搜索树的应用
1.5 二叉搜索树的性能分析
2.二叉树进阶经典题：
1.二叉搜索树
1.1 二叉搜索树概念
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值若它的右子树不为空，则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树
二叉搜索树又称二叉排序树，因为根据其性质我们可以知道其中序遍历是有序的。
1.2 二叉搜索树操作
1. 二叉搜索树的查找a 、从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。b 、最多查找高度次，走到到空，还没找到，这个值不存在。2. 二叉搜索树的插入插入的具体过程如下：a. 树为空，则直接新增节点，赋值给 root 指针b. 树不空，按二叉搜索树性质查找插入位置，插入新节点3.二叉搜索树的删除首先查找元素是否在二叉搜索树中，如果不存在，则返回 , 否则要删除的结点可能分下面四种情 况：a. 要删除的结点无孩子结点b. 要删除的结点只有左孩子结点c. 要删除的结点只有右孩子结点d. 要删除的结点有左、右孩子结点删除方法：看起来有待删除节点有 4 中情况，实际情况 a 可以与情况 b 或者 c 合并起来，因此真正的删除过程如下：情况 b ：删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点 -- 直接删除情况 c ：删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点 -- 直接删除情况 d ：在它的 右子树中寻找中序下的第一个结点(关键码最小) ，用它的值填补到被删除节点中，再来处理该结点的删除问题 -- 替换法删除
1.3 二叉搜索树的实现
这里使用递归版本和非递归版本进行实现，需要注意的是为了保证封装性，这里大多采用子函数的形式来防止封装性被破坏。其中删除的过程最复杂
//节点类
template <class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
};
//二叉搜索树
template <class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
//为了不破坏封装性，采用子函数的形式不暴露根
BSTree(const BSTree<K>& t)
{
_root = CopyTree(t._root);
}
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root,t._root);
return *this;
}
~BSTree()
{
Destroy(_root);
_root = nullptr;
}
//插入
bool Insert(const K& key)
{
//开始插入第一个的情况
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//不允许插入相同的值
return false;
}
}
cur = new Node(key);
//判断链接的左右
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
//查找
bool Find(const K& key)
{
if (_root == nullptr)
return false;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
//删除
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//找到了
//1.可能是左为空
//2.右为空
//两边都不为空
if(cur->_left == nullptr)
{
//有可能删除根节点
if (cur == _root)
{
_root = _root->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = _root->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
//都不为空
//从当前节点的右子树开始找最小的值
Node* minright = cur->_right;
Node* parent = cur;
while (minright->_left)
{
parent = minright;
minright = minright->_left;
}
cur->_key = minright->_key;
//将最小的值的节点剩下的节点链接给parent
if (parent->_left == minright)
{
parent->_left = minright->_right;
}
else
{
parent->_right = minright->_right;
}
delete minright;
}
return true;
}
}
return false;
}
//打印,为了保证其封装性，可以使用子函数,采用中序遍历
void Print()
{
PrintHelper(_root);
}
//递归版本的插入
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
//递归版本的查找
bool FindR(const K& key)
{
return _FindR(_root, key);
}
//递归版本的删除
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
void Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
Node* CopyTree(Node* root)
{
//前序建树即可
if (root == nullptr)
{
return true;
}
Node* newRoot = new Node(root->_key);
newRoot->_left = CopyTree(root->_left);
newRoot->_right = CopyTree(root->_right);
return newRoot;
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
//找到，删除
Node* del = root;
//还是分3种情况
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
//在当前节点的右子树找到最小值，然后交换
Node* minright = root->_right;
while (minright->_left)
{
minright = minright->_left;
}
//交换
swap(minright->_key, root->_key);
//在右子树中找到要删除的值
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key > key)
{
return _FindR(root->_left, key);
}
else if (root->_key < key)
{
return _FindR(root->_right, key);
}
else
{
return true;
}
}
bool _InsertR(Node*& root,const K& key)
{
if (root == nullptr)
{
//插入,因为这里是引用，所以直接赋值即可
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
//相同
return false;
}
}
void PrintHelper(const Node* _root)
{
//中序遍历
if (_root == nullptr)
return;
PrintHelper(_root->_left);
cout << _root->_key << " ";
PrintHelper(_root->_right);
}
Node* _root = nullptr;
};1.4 二叉搜索树的应用
1. K 模型： K 模型即只有 key 作为关键码，结构中只需要存储 Key 即可，关键码即为需要搜索到 的值 。比如： 给一个单词 word ，判断该单词是否拼写正确 ，具体方式如下：以词库中所有单词集合中的每个单词作为 key ，构建一棵二叉搜索树在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。2. KV模型 ：每一个关键码 key ，都有与之对应的值 Value ，即 <Key, Value> 的键值对 。该种方式在现实生活中非常 常见 ：比如 英汉词典就是英文与中文的对应关系 ，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文 <word, chinese> 就构成一种键值对；再比如 统计单词次数 ，统计成功后，给定单词就可快速找到其出现的次数， 单词与其出现次数就是 <word, count> 就构成一种键值对
KV模型代码变形：（这里只修改了插入和查找，因为这个使用的多，而且到后面的map和set会深入学习）
//改造二叉搜索树变为KV模型
namespace KV
{
template <class K, class V>
struct BSTreeNode
{
BSTreeNode<K,V>* _left;
BSTreeNode<K,V>* _right;
K _key;
V _val;
BSTreeNode(const K& key, const V& val)
:_key(key)
, _val(val)
, _left(nullptr)
, _right(nullptr)
{}
};
template <class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
//插入
bool Insert(const K& key, const V& val)
{
//开始插入第一个的情况
if (_root == nullptr)
{
_root = new Node(key,val);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//不允许插入相同的值
return false;
}
}
cur = new Node(key,val);
//判断链接的左右
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
//查找
Node* Find(const K& key)
{
if (_root == nullptr)
return nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
return cur;
{
}
}
return nullptr;
}
private:
Node* _root = nullptr;
};
}下面就是KV模型的两个例子：
1.在字典中查找你写的单词是否存在：
void TestBSTree1()
{
BSTree<string, string> dict;
dict.Insert("string", "字符串");
dict.Insert("tree", "树");
dict.Insert("left", "左边、剩余");
dict.Insert("right", "右边");
dict.Insert("sort", "排序");
string str;
while (cin >> str)
{
//在字典中查找
BSTreeNode<string,string>* ret = dict.Find(str);
if (ret)
{
cout << ret->_val << endl;
}
else
{
cout << "不存在" << endl;
}
}
}看看结果：
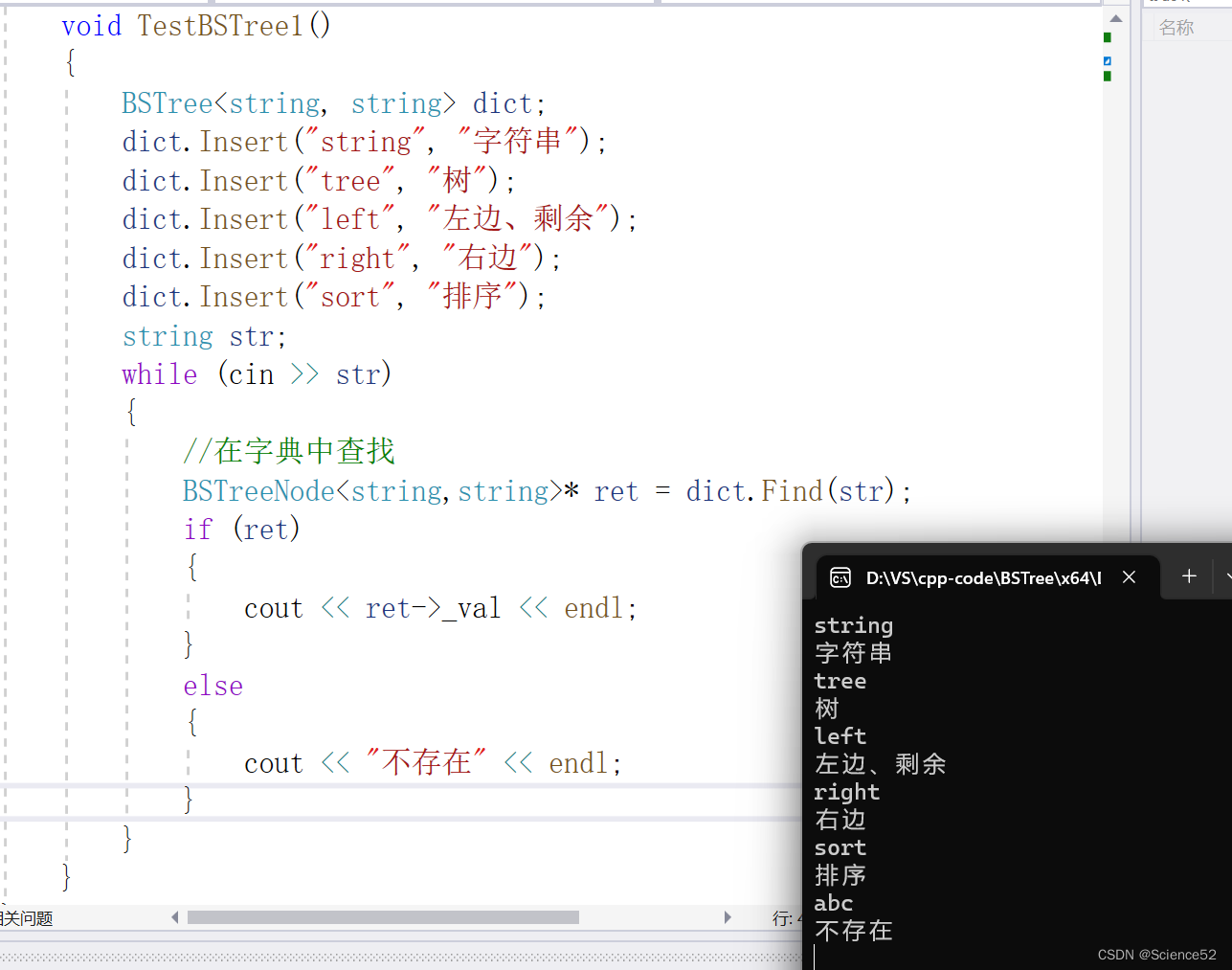
2.统计次数：（常用）：
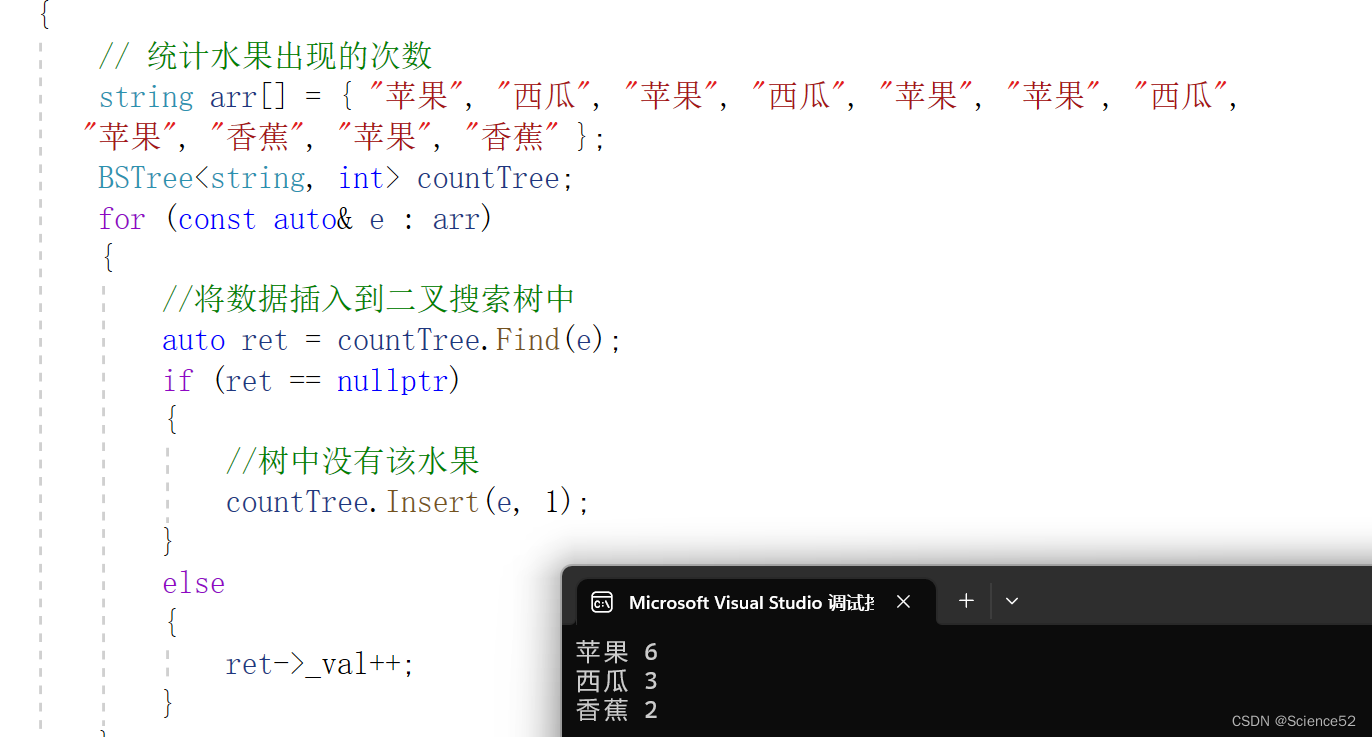
void TestBSTree2()
{
// 统计水果出现的次数
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉" };
BSTree<string, int> countTree;
for (const auto& e : arr)
{
//将数据插入到二叉搜索树中
auto ret = countTree.Find(e);
if (ret == nullptr)
{
//树中没有该水果
countTree.Insert(e, 1);
}
else
{
ret->_val++;
}
}
countTree.Print();
}结果：
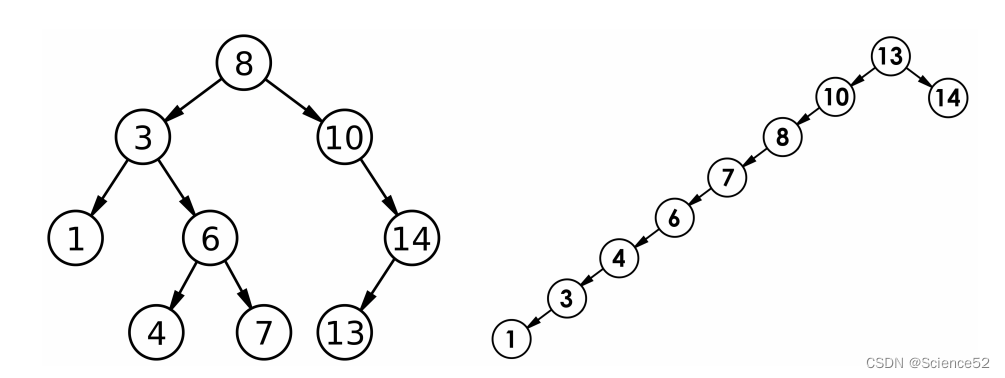
1.5 二叉搜索树的性能分析
插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有
n
个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
最优情况下
，二叉搜索树为完全二叉树
(
或者接近完全二叉树
)
，其平均比较次数为：
logN
最差情况下
，二叉搜索树退化为单支树
(
或者类似单支
)
，其平均比较次数为：
N
后面我们学习了AVL树以及红黑树就可以使二叉搜索树的效率达到最高了。
2.二叉树进阶经典题：
1.根据二叉树创建字符串
思路：根据前序遍历，我们可以通过根左子树右子树的顺序进行递归，但是递归子树的时候需要注意条件，如果左子树是空，但是有右子树就需要保留空括号，如果左子树不为空，但右子树为空，就不需要保留空括号。
class Solution {
public:
void _tree2str(TreeNode* root,string& result)
{
if(root == nullptr)
{
result += "";
return;
}
result += to_string(root->val);
if(root->left || root->right)
{
result += "(";
_tree2str(root->left,result);
result += ")";
}
if(root->right)
{
result += "(";
_tree2str(root->right,result);
result += ")";
}
}
string tree2str(TreeNode* root) {
string result;
_tree2str(root,result);
return result;
}
};2.二叉树的层序遍历
思路：我们可以通过队列来模拟层序遍历：一次输入一层的节点，然后把队列中当层的元素全部弹出，同时进入下一层元素，我们可以通过size来控制当层元素的个数。然后把当层元素放入结果集中
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
if(root == nullptr)
return result;
queue<TreeNode*> q;
q.push(root);
while(!q.empty())
{
vector<int> tmp;
int size = q.size();
while(size--)
{
TreeNode* frontnode = q.front();
q.pop();
tmp.push_back(frontnode->val);
//放入左右节点
if(frontnode->left)
{
q.push(frontnode->left);
}
if(frontnode->right)
{
q.push(frontnode->right);
}
}
result.push_back(tmp);
}
return result;
}
};3.二叉树的最近公共祖先
思路：这题可以使用回溯法来解决，我们可以分别将p和q的路径存放在栈中，然后通过对栈的弹出操作，找到他们相同的节点。其中找路径问题就是回溯问题，我们可以把每次递归的结果先保存起来，如果找到就返回真，就可以结束递归，如果没有找到我们就继续递归，当子树递归到了nullptr时，我们就需要回退，回退的本质就是将栈顶元素pop。
class Solution {
public:
bool _lowestCommonAncestor(TreeNode* root,TreeNode* p,stack<TreeNode*>& st)
{
if(root == nullptr)
{
return false;
}
st.push(root);
if(root == p)
{
return true;
}
if(_lowestCommonAncestor(root->left,p,st))
{
return true;
}
if(_lowestCommonAncestor(root->right,p,st))
{
return true;
}
//回退
st.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//回溯法
stack<TreeNode*> pv;
stack<TreeNode*> qv;
_lowestCommonAncestor(root,p,pv);
_lowestCommonAncestor(root,q,qv);
while(pv.size() != qv.size())
{
if(pv.size() > qv.size())
{
pv.pop();
}
else
qv.pop();
}
while(pv.top() != qv.top())
{
pv.pop();
qv.pop();
}
return pv.top();
}
};4.二叉搜索树与双向链表
思路：因为二叉搜索树的中序是有序的，我们可以先递归到最小的节点，然后通过中序改变它们之间的链接关系。
class Solution {
public:
void _Convert(TreeNode* cur,TreeNode*& prev)
{
if(cur == nullptr)
{
return;
}
//中序走到最小
_Convert(cur->left,prev);
//建立链接关系
//这里是防止第一次prev为空的情况
if(prev)
{
prev->right = cur;
}
cur->left = prev;
prev = cur;
_Convert(cur->right,prev);
}
TreeNode* Convert(TreeNode* root) {
if(root == nullptr)
return nullptr;
TreeNode* prev = nullptr;
_Convert(root,prev);
//返回根
while(root->left)
{
root = root->left;
}
return root;
}
};
5.从前序与中序遍历序列构造二叉树
思路：因为前序是可以确定根的，所以我们可以在中序中找到根，然后划分左右子树的区间，根据前序的顺序，先递归左子树，再递归右子树，当区间不存在时即可回退。
class Solution {
public:
TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int begin,int end,int& i)
{
if(begin > end)
return nullptr;
//从中序中找子树区间
int j = begin;
for(;j<=end;++j)
{
if(inorder[j] == preorder[i])
break;
}
TreeNode* root = new TreeNode(preorder[i++]);
//[begin,j-1] j [j+1,end]
root->left = _buildTree(preorder,inorder,begin,j-1,i);
root->right = _buildTree(preorder,inorder,j+1,end,i);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
//先序找根，中序找子树
//采用闭区间
int i = 0;
return _buildTree(preorder,inorder,0,inorder.size()-1,i);
}
};6.使用非递归实现二叉树的前序遍历
思路：一般递归可以实现的代码，使用非递归都需要使用到数据结构的栈，我们可以将树分成左路节点和右树，我们先迭代左路节点到空，其中把每个值存放在栈中，并保存到结果集中，然后取栈顶元素再走右树即可。而中序遍历所需要保存的结果刚好是前序遍历栈弹出的结果，代码与这个类似。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
//分成两部分，左路节点和右子树
TreeNode* cur = root;
stack<TreeNode*> st;
vector<int> v;
while(!st.empty() || cur)
{
while(cur)
{
v.push_back(cur->val);
st.push(cur);
cur = cur->left;
}
//走右子树
TreeNode* tmp = st.top();
st.pop();
cur = tmp->right;
}
return v;
}
};7.使用非递归实现二叉树的后序遍历
思路：这个和前序以及中序有所不同，就是在确定根的时候，我们需要确定两次，第一次是拿到根并走其右子树，第二次拿到根的时候就可以将根从栈中弹出了。我们也可以使用结构体存放每个节点和节点被取出的次数。当然还有更巧妙的方法：当我们走到右子树的最右端时，我们就可以使用一个指针记录下来，在当前节点回退的时候必然存在cur->right == prev（这个就是用来记录的节点），然后我们再把这个标记节点更新到当前节点，这样就可以不断回退了。具体看代码理解：
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* prev = nullptr;//用来记录根的右子树是否被访问
while(!st.empty() || cur)
{
while(cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
//如果右子树为空或者到最右端返回的时候就回收结果
if(top->right == nullptr || top->right == prev)
{
st.pop();
v.push_back(top->val);
prev = top;//从最右端回来的时候起重要作用
}
else
{
//这时候要往右迭代
cur = top->right;
}
}
return v;
}
};
