文章目录

前言
1. Set / Map接口
2. TreeSet类
3. TreeMap 类
4. HashSet 与 HashMap
- 4.1 HashSet / HashMap 底层哈希表
- 4.2 解决哈希冲突
总结

✨✨✨学习的道路很枯燥，希望我们能并肩走下来！

编程真是一件很奇妙的东西。你只是浅尝辄止，那么只会觉得枯燥乏味，像对待任务似的应付它。但你如果深入探索，就会发现其中的奇妙，了解许多所不知道的原理。知识的力量让你沉醉，甘愿深陷其中并发现宝藏。

前言

本篇是介绍数据结构Set与Map接口，了解TreeMap,HashMap,TreeSet,HashSet类；如有错误，请在评论区指正，让我们一起交流，共同进步！

本文开始

1. Set / Map接口

Set接口继承Collection，Map是独立的接口
进一步认识TreeSet和TreeMap就需要知道底层搜索树是如何查找，插入，删除的；
红黑树过于复杂，先认识一下简单的二叉搜索树，为以后学习做一个铺垫；

简单二叉搜索树特点：
左孩子 < 根节点，右孩子 > 根节点；

简单二叉搜索树查找代码：

//查找key是否存在: 二叉搜索树特点：左孩子小于根节点，右孩子大于根节点
    public TreeNode search(int key) {
        //重新定义访问的头节点
        TreeNode cur = root;
        //遍历二叉树，查找值
        while (cur != null) {
            if(cur.key == key) {
                return cur;
            }else if(cur.key < key) {
                //节点值大于查找值
                cur = cur.right;
            }else {
                //节点值小于查找值
                cur = cur.left;
            }
        }
        return null;//没找到
    }

简单二叉搜索树插入代码：

    //定义根节点
    public TreeNode root;
    //插入一个元素：发现插入二叉搜索树的元素都会插入叶子节点
    public boolean insert(int key) {
   		 //空树直接插入
        if(root == null) {
            root = new TreeNode(key);
            return true;
        }
        TreeNode cur = root;
        TreeNode parent = null;
        //遍历, 并记录父节点位置；
        //真正找到插入位置，cur==null无法插入，就需要记录它的父节点
        while (cur != null) {
            if(cur.key < key) {
                //先记录父节点
                parent = cur;
                cur = cur.right;
            }else if(cur.key == key) {
                //插入一样的直接返回
                return false;
            }else {
                 //cur.key > key
                parent = cur;
                cur = cur.left;
            }
        }
        //找到位置，判断在父节点左还是右
        if(parent.key < key) {
            parent.right = new TreeNode(key);
        }else {
            parent.left = new TreeNode(key);
        }
        return true;
    }

简单二叉搜索树删除代码：
删除的7种情况：
删除节点左为空：是否为根节点；不为根节点，是父节点的左孩子还是右孩子（3种）
删除节点右为空：是否为根节点；不为根节点，是父节点的左孩子还是右孩子（3种）
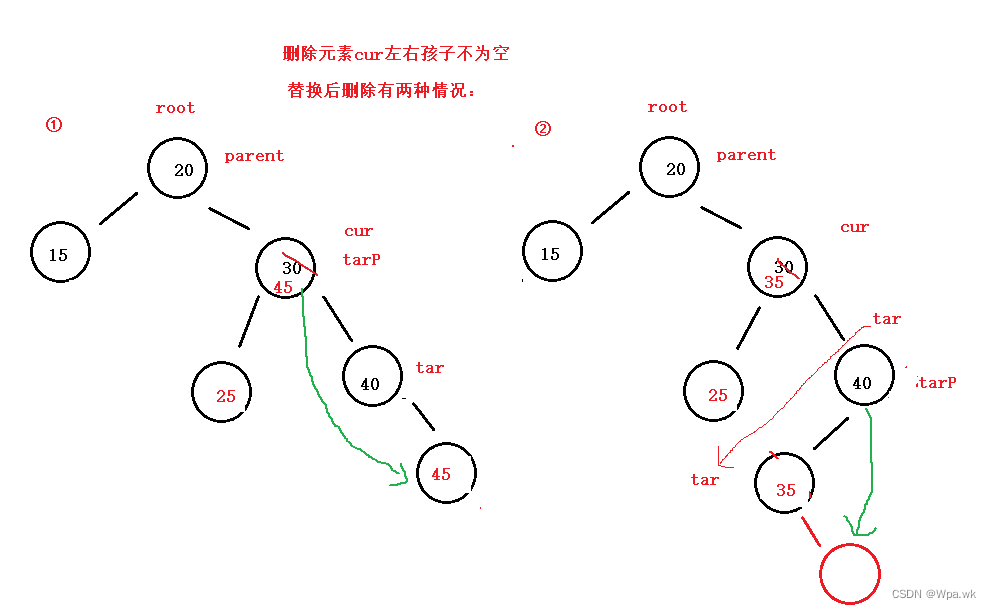
删除节点左右都不为空：替换法，右树最小值与删除值替换或者左树最大值替换；最后删除替换的值；（1种）

 //删除key的值
    public boolean remove(int key) {
        TreeNode cur = root;
        TreeNode parent = null;//记录父节点，删除的情况复杂需要判断
        //先找到删除节点位置
        while (cur != null) {
            if(cur.key < key) {
                parent = cur;
                cur = cur.right;
            }else if(cur.key == key) {
                removeNode(parent,cur);
                return true;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        return false;
    }
    //cur: 为删除节点位置，parent:为删除节点的父节点位置
    private void removeNode(TreeNode parent, TreeNode cur) {
        //判断删除节点左右是否为空
        if(cur.left == null) {
            //左为空，在判断的是否为根节点
            if(cur.key == root.key) {
                //删除节点为根节点，直接移动根节点即可
                root = cur.right;
            }else if(cur == parent.left) {
                //删除节点不为根，为父节点的左位置
                parent.left = cur.right;
            }else {
                //删除节点不为根，为父节点的右位置
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            //右为空，在判断的是否为根节点
            if(cur.key == root.key) {
                //删除节点为根节点，直接移动根节点即可
                root = cur.left;
            }else if(cur == parent.left) {
                //删除节点不为根，为父节点的左位置
                parent.left = cur.left;
            }else {
                //删除节点不为根，为父节点的右位置
                parent.right = cur.left;
            }
        }else {
            //删除节点左右孩子都不为空
            //使用替换法，记录该位置tarP,在其右子树找到最小值与删除值替换
            TreeNode tar = cur.right;
            TreeNode tarP = cur;
            //找右树最小值
            while (tar.left != null) {
                tarP = tar;
                tar = tar.left;
            }
            //替换
            cur.key = tar.key;
            //替换后删除tar位置
            if(tarP.left == tar) {
                tarP.left = tar.right;
            }else {
                //可能没有左子树位置
                tarP.right = tar.right;
            }
        }
    }

2. TreeSet类

TreeSet是Set接口的实现类，它的底层是一颗搜索树（红黑树），红黑树是一颗高度平衡的二叉搜索树；
时间复杂度：O(logn); - 这里是以2为底的
特点：只能存储key，重复的值集合中不添加

Set 集合方法代码测试：

public static void main(String[] args) {
        Set<Integer> set = new TreeSet<>();
        //Set里增加 key - 且不重复添加
        set.add(1);
        set.add(2);
        set.add(1);
        set.add(3);
        System.out.println(set);
        //判断Set集合中是否存在key
        if(set.contains(2)) {
            System.out.println("存在");
        }
        //删除集合中的值 - key
        set.remove(1);
        System.out.println(set);
        //set集合是否为空
        System.out.println(set.isEmpty());
        //判断set集合大小
        System.out.println(set.size());
        //判断集合中的元素是否在set中全部存在
        List<Integer> list = new ArrayList<>();
        list.add(3);
        list.add(2);
        System.out.println(set.containsAll(list));
        //将集合添加到set去重
        List<Integer> list2 = new ArrayList<>();
        list2.add(4);
        list2.add(4);
        set.addAll(list2);
        System.out.println(set);
        //迭代器打印set集合
        Iterator<Integer> it = set.iterator();
        while (it.hasNext()) {
            System.out.print(it.next() + " ");
        }
        System.out.println();
    }

3. TreeMap 类

TreeMap : 底层也是搜索树 - 红黑树；
时间复杂度：O(logn)
特点：存储 key-val, key值唯一且不为空null，val值可替换；key-val可用null值
Map集合的常用方法：
【注】 map中的entrySet() =》每个元素类型 Entry<T,V> entry
entrySet获得所有键值对，可用getKey,getValue获取键或值；

public static void main(String[] args) {
        Map<String,Integer> map = new TreeMap<>();
        //Map集合中增加值
        map.put("a",1);
        map.put("ab",3);
        //map.put("ab",4);
        map.put("abc",2);
        map.put("abd",2);
        //Map集合根据key,获得val
        System.out.println(map.get("a"));
        //key不存在，返回默认值
        System.out.println(map.getOrDefault("c", 666));
        //map集合中的keySet(): 返回集合中所有不重复的key
        for (String s : map.keySet()) {
            System.out.print(s + " ");
        }
        System.out.println();
        //s
        // map.values将集合中的val返回 - val可重复
        for (int x : map.values()) {
            System.out.print(x + " ");
        }
        System.out.println();
        //entrySet() - 返回集合中的所有key-val
        for (Map.Entry<String,Integer> entry : map.entrySet()) {
            System.out.println(entry.getKey() + "---" + entry.getValue());
        }
        //移除map集合中的值,返回被移除的值val
        System.out.println(map.remove("ab"));
        //判断是否包含key
        System.out.println(map.containsKey("abc"));
    }

4. HashSet 与 HashMap

4.1 HashSet / HashMap 底层哈希表

HashSet / HashMap: 底层是哈希表一种数组 + 链表 + 红黑树的结构
时间复杂度：O(1)
哈希表特点：数组中存储每个链表的头节点，根据源码，当链表长度超过8，数组长度超过64，链表会变成红黑树；
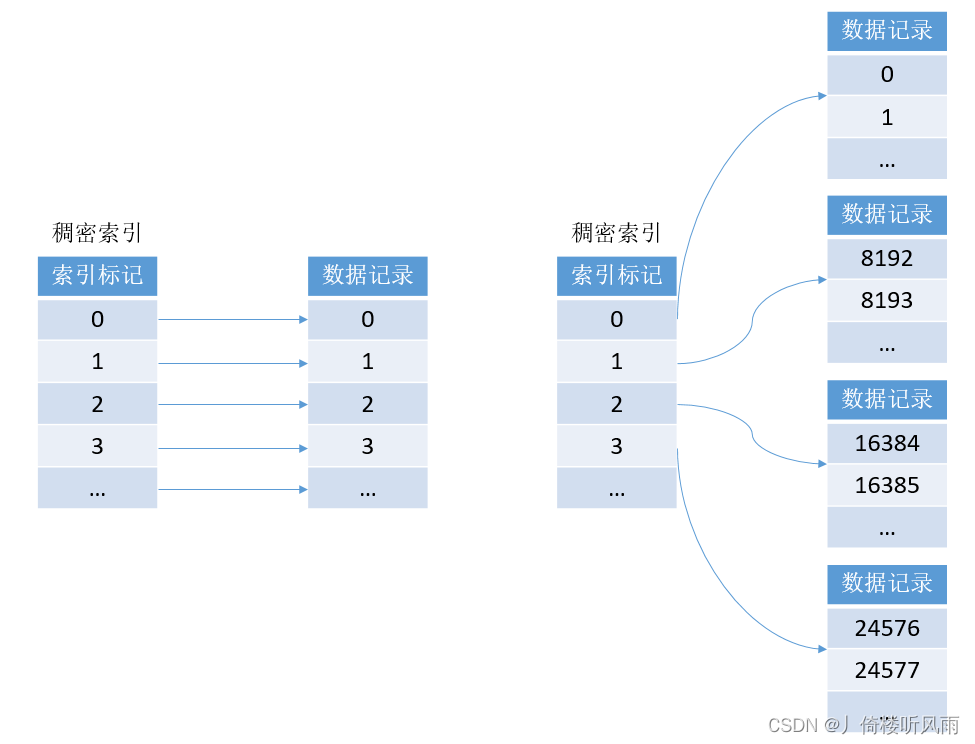
哈希表：在数组中插入元素，需要根据得到的哈希函数得到在数组中的存储地址存储元素，例如：存储元素 / 数组长度 = 数组中存储地址；

计算哈希地址，可能得到一样的地址，就会产生哈希冲突 <=>地址冲突（地址一样）

接下来看一下如何解决？

4.2 解决哈希冲突

方式一：闭散列（开地址法）
①线性探测：
存入数组的数字为3，33，根据 哈希函数(index = 插入的数字 % 数组长度) 得到的余数下标插入，假设长度为10，3插在3位置，33根据哈希函数得到的位置也是3位置，在3位置之后依次寻找没有插入的位置插入即可（3位置后面有地方就插入，没有就接着往后找）；

②二次探测：
当根据哈希函数找到地址一样时（哈希冲突），找下一个地址根据Hi = (H0 + i^2) % len; (i = 1,2,3…), Hi => 下一个地址，H0 => 根据哈希函数计算得到的位置，len: 数组长度；

方式二：开散列（链地址法）
哈希表：一个数组，数组中每个元素存储单链表的头节点（每个元素都是链表）；

代码实现简单的哈希桶：实现put(插入),get(获取)方法

public class HashBucket {
    //数组每个元素为链表，链表每个元素为节点 =》定义节点
    private static class Node {
        private int key;
        private int value;
        Node next;

        public Node(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }

    private Node[]  array;
    private int size;   // 当前的数据个数
    private static final double LOAD_FACTOR = 0.75;//默认的负载因子，不能超过0.75
    private static final int DEFAULT_SIZE = 8;//默认桶的大小,扩容时需要

    public int put(int key, int value) {
        //获取插入的地址：根据哈希函数计算
        //除留余数法
        int index = key % array.length;
        //找到位置，遍历该位置链表，元素是否插入过
        Node cur = array[index];//重头遍历
        while (cur != null) {
            //判断元素是否一样
            if(cur.key == key) {
                //找到，就更新
                cur.value = value;
                return cur.value;
            }
            cur = cur.next;
        }
        //没找到一样的，头插元素
        Node node = new Node(key,value);
        node.next = array[index];
        array[index] = node;//移动头节点
        size++;//计数+1
        //判断是否需要扩容: 超过负载因子需要扩容
        if(loadFactor() > LOAD_FACTOR) {
            resize();
        }
        return cur.value;
    }


    private void resize() {
        //扩容时数组长度改变，会产生新的插入位置，所以原数组中所有元素需要重新插入
        //扩容
        Node[] newArr = new Node[2*array.length];
        //遍历原来数组
        for (int i = 0; i < array.length; i++) {
            Node cur = array[i];//每个链表的头节点
            //就地址更改进新数组
            while (cur != null) {
                //记录下一个节点位置
                Node curNext = cur.next;
                //获取插入新数组中的地址
                int index = cur.key % newArr.length;
                //重新头插
                cur.next = newArr[index];
                newArr[index] = cur;
                cur = curNext;
            }
        }
        array = newArr;//新数组给旧数组，扩容完毕
    }

    //计数当前负载因子：数组中元素个数 / 数组长度；
    private double loadFactor() {
        return size * 1.0 / array.length;
    }


    public HashBucket() {
        //初始化数组可以存储几个元素
        Node[] array = new Node[10];
    }

    public int get(int key) {
        //获取得到节点下标
        int index = key % array.length;
        Node cur = array[index];
        while (cur != null) {
            //判断是否得到节点
            if(cur.key == key) {
                //得到返回值
                return cur.value;
            }
            cur = cur.next;
        }
        return -1;//没找到
    }
}