电子技术——共模抑制

我们在之前学习过，无论是MOS还是BJT的差分输入对，共模信号并不会改变漏极电流的大小，因此我们说差分输入对共模信号无响应。但是实际上由于各种客观非理想因素，例如电流源有限阻抗等，此时共模是影响差分输入对的。

MOS的情况

$R_{SS}$ 的影响

下图是一个MOS的差分输入对，但是电流源是有限阻抗的，阻抗大小为 $R_{SS}$ ，而且我们输入端有两个电压，一是信号本身固有的共模电压 $V_{CM}$ ，另外一个是外界干扰的共模电压 $v_{icm}$ 可能是干扰信号，也可能是噪波。我们的目的就是讨论 $v_{icm}$ 对输出电压的影响：

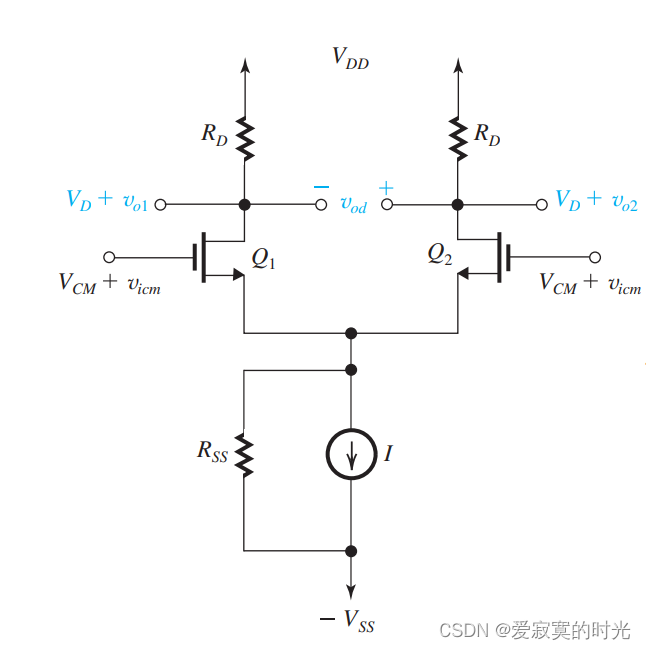
首先我们讨论一下 $R_{SS}$ 对偏置的影响，由于 $R_{SS}$ 的存在，流过MOS的电流要比 $I/2$ 稍稍大一些。然而一般情况下 $R_{SS}$ 都是非常巨大的，因此超出 $I/2$ 的那一部分几乎可以忽略。其次 $R_{SS}$ 对 $A_d$ 也是没有影响的，这是因为假设MOS都是完全相同的，此时源极永远都是虚拟地， $R_{SS}$ 无影响。

现在我们讨论 $v_{icm}$ 存在的影响，考虑下面的电路：

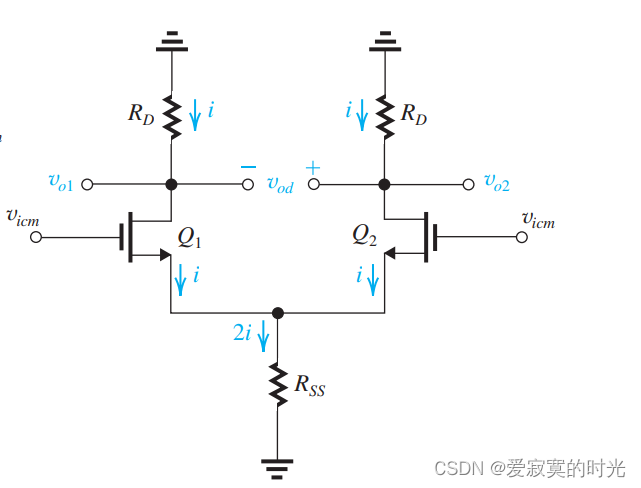
我们移除了所有的DC分量，只考虑信号作用，此时电路仍然是完全对称的，我们将MOS的漏极信号电流记为 $i$ 则流过 $R_{SS}$ 的电流为 $2i$ 。我们使用等效T模型分析：

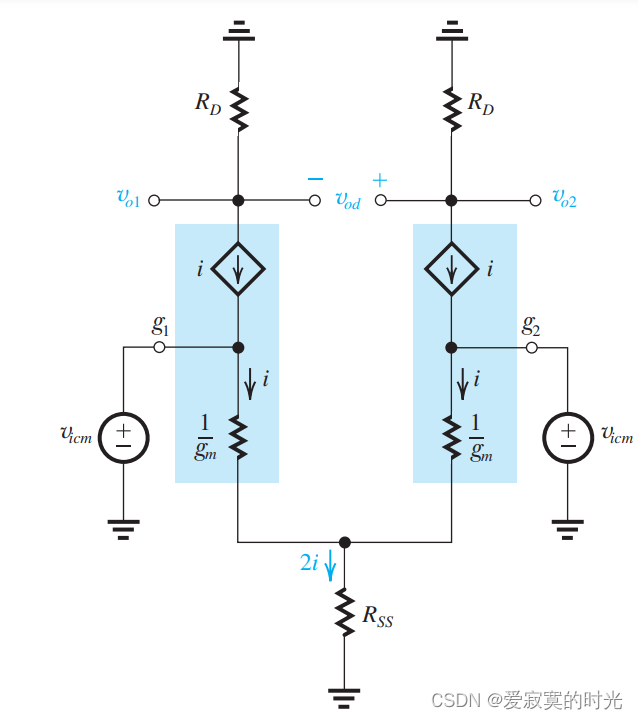
则有：

$$v_{icm}=\frac{i}{g_m}+2i{R}_{SS}$$

所以：

$$i=\frac{v_{icm}}{1/g_m+2R_{SS}}$$

输出信号电压为：

$$v_{o1}=v_{o2}=-\frac{R_D}{1/g_m+2R_{SS}}{v}_{icm}$$

这就说明 $v_{o1}$ 和 $v_{o2}$ 是受 $v_{icm}$ 影响的，影响的比例大约为：

$$\frac{v_o}{v_{icm}}\simeq -\frac{R_D}{2R_{SS}}$$

这里我们假设 $2R_{SS}\gg 1/g_m$ ，尽管如此，其差分输出信号仍然为零。

$$v_{od}=v_{o2}-v_{o1}=0$$

MOS差分输入对抑制了全部的共模信号，是我们想要的结果。但是事实上并不总是如此，特别是电路不对称的情况。由于现在电路的对称性，我们仍然可以使用半电路分析：

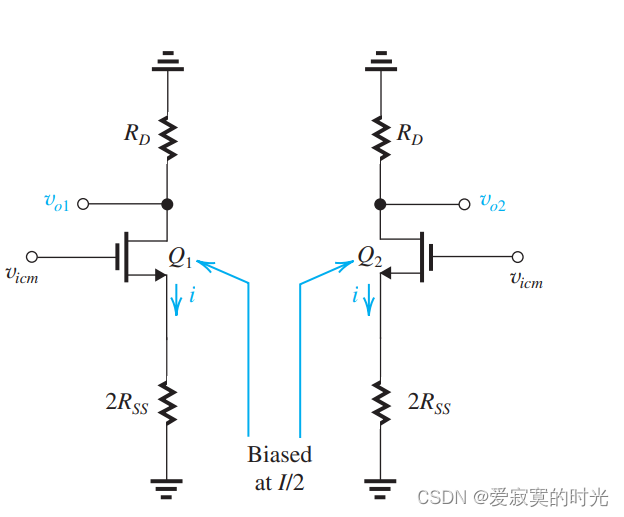
这种半电路我们称为 共模半电路 。

$R_D$ 不匹配的影响

另一种非理想因素是 $R_D$ 不匹配，我们假设 $Q_1$ 为 $R_D$ 而 $Q_2$ 为 $R_D+\Delta R_D$ ，此时的输出端信号电流为：

$$v_{o1}\simeq -\frac{R_D}{2R_{SS}}{v}_{icm}$$

$$v_{o2}\simeq -\frac{R_D+\Delta R_D}{2R_{SS}}{v}_{icm}$$

所以差分信号电压为：

$$v_{od}=v_{o2}-v_{o1}=-\frac{\Delta R_D}{2R_{SS}}{v}_{icm}$$

我们记其 共模增益 为：

$$A_{cm}\equiv \frac{v_{od}}{v_{icm}}=-\frac{\Delta R_D}{2R_{SS}}$$

还可以表示为：

$$A_{cm}=-(\frac{R_D}{2R_{SS}})(\frac{\Delta R_D}{R_D})$$

这说明 $R_D$ 不匹配会影响 $v_{od}$ 的输出，即 $v_{od}$ 存在 $v_{icm}$ 分量，这个分量是我们不想要的。为了衡量 $v_{icm}$ 的占比，我们引入 共模抑制比 定义为：

$$CMRR\equiv \frac{|A_d|}{|A_{cm}|}$$

经常使用分贝来表示：

$$CMRR(dB)=20\log \frac{|A_d|}{|A_{cm}|}$$

$R_D$ 不匹配带来的共模抑制比为：

$$CMRR=(2g_m{R}_{SS})/(\frac{\Delta R_D}{R_D})$$

为了获得更大的共模抑制比，我们可以增大偏置电流，或者增大电流源输出阻抗，以及尽可能使得电路匹配，即 $(\frac{\Delta R_D}{R_D})$ 尽量小。

$g_m$ 不匹配的影响

另外一种非理想因素是两个MOS管本身不匹配，可以看做是 $g_m$ 不匹配的影响。我们假设：

$$g_{m1}=g_m+\frac{1}{2}\Delta g_m$$

$$g_{m2}=g_m-\frac{1}{2}\Delta g_m$$

也就是：

$$g_{m1}-g_{m2}=\Delta g_m$$

虽然此时电路不对称，我们无法使用半电路法分析，我们可以使用直接计算得到：

$$A_{cm}\simeq (\frac{R_D}{2R_{SS}})(\frac{\Delta g_m}{g_m})$$

则共模抑制比为：

$$CMRR=(2g_m{R}_{SS})/(\frac{\Delta g_m}{g_m})$$

这个形式和 $R_D$ 不匹配的影响一样。同样的为了获得更大的共模抑制比，我们可以增大偏置电流，或者增大电流源输出阻抗，以及尽可能使得电路匹配，即 $(\frac{\Delta g_m}{g_m})$ 尽量小。

差分输出和单端输出

以上的讨论都是基于差分输出而言的，如果使用的是单端输出，则CMRR会大大降低，这是因为在本节一开始我们就分析了，即使如果电路是对称的，那么 $v_{icm}$ 也会出现在输出端的两端，如果使用单端输出 $v_{icm}$ 就会出现在输出电压上。如果我们想获得较大的CMRR，我们推荐使用差分输出。之后我们会介绍如何保持CMRR无损的将差分信号转换为单端信号。

BJT的情况

同样对于BJT也存在共模抑制的情况，我们使用如下图的电路以及对应的半电路：

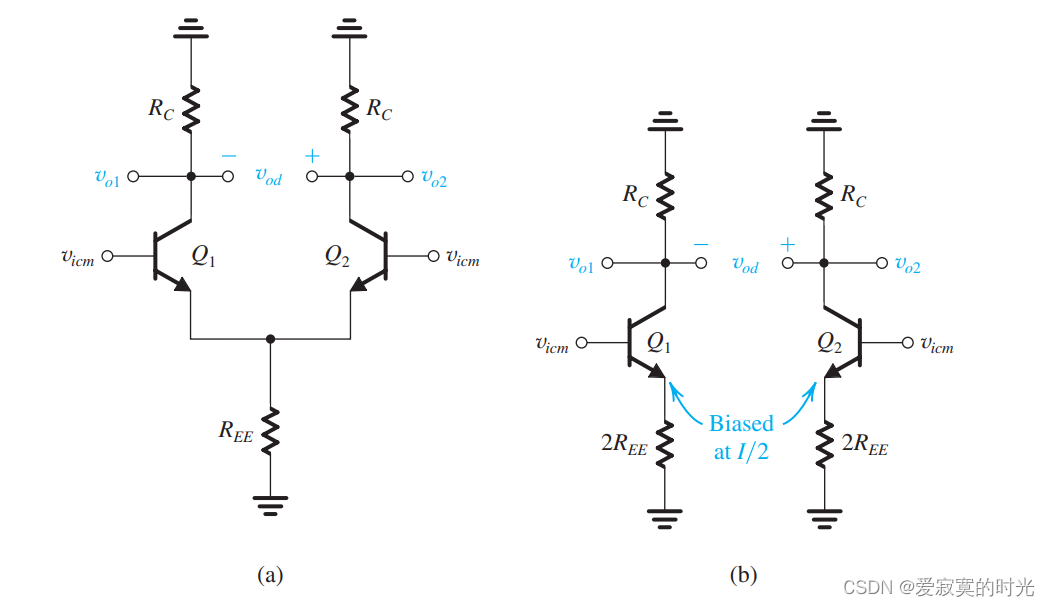
输出信号电压为：

$$v_{o1}=v_{o2}=-\frac{\alpha R_C}{r_e+2R_{EE}}{v}_{icm}$$

说明BJT的同样抑制共模信号。但是当出现电路不匹配的情况下，例如存在 $\Delta R_C$ ：

$$A_{cm}=-\frac{\alpha \Delta R_C}{2R_{EE}+r_e}$$

因为 $\alpha \simeq 1,r_e\ll 2R_{EE}$ 所以：

$$A_{cm}\simeq -(\frac{R_C}{2R_{EE}})(\frac{\Delta R_C}{R_C})$$

因此共模抑制比为：

$$CMRR=(2g_m{R}_{EE})/(\frac{\Delta R_C}{R_C})$$

与MOS具有相同的形式。

BJT的输入阻抗是有限的，因此对于 $v_{icm}$ 来说也存在输入阻抗，如图：

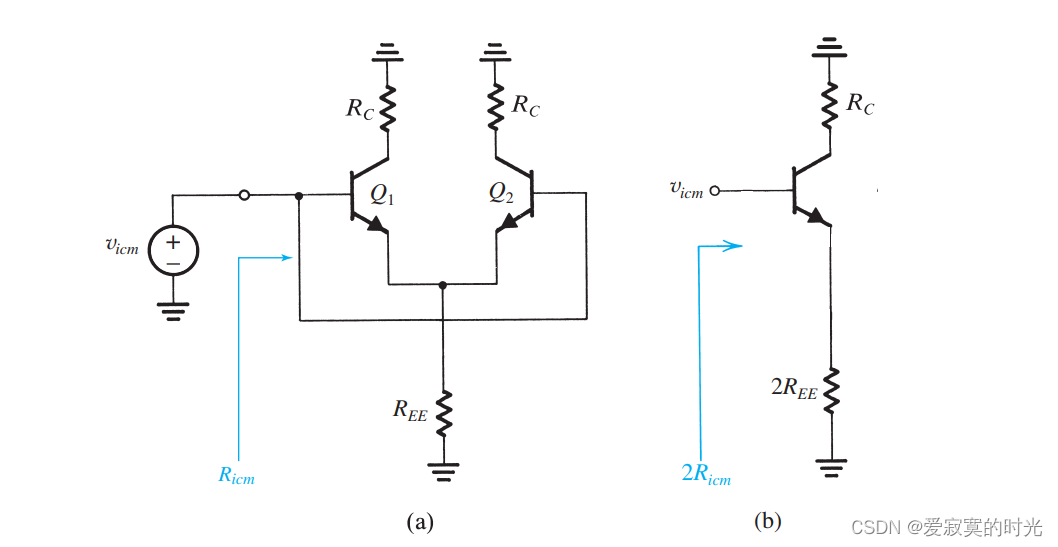
我们定义 $R_{icm}$ 是共模信号的输入阻抗，对应的等效半电路输入阻抗为 $2R_{icm}$ 我们有：

$$R_{icm}\simeq \beta R_{EE}\frac{1+R_C/\beta r_o}{1+\frac{R_C+2R_{EE}}{r_o}}$$