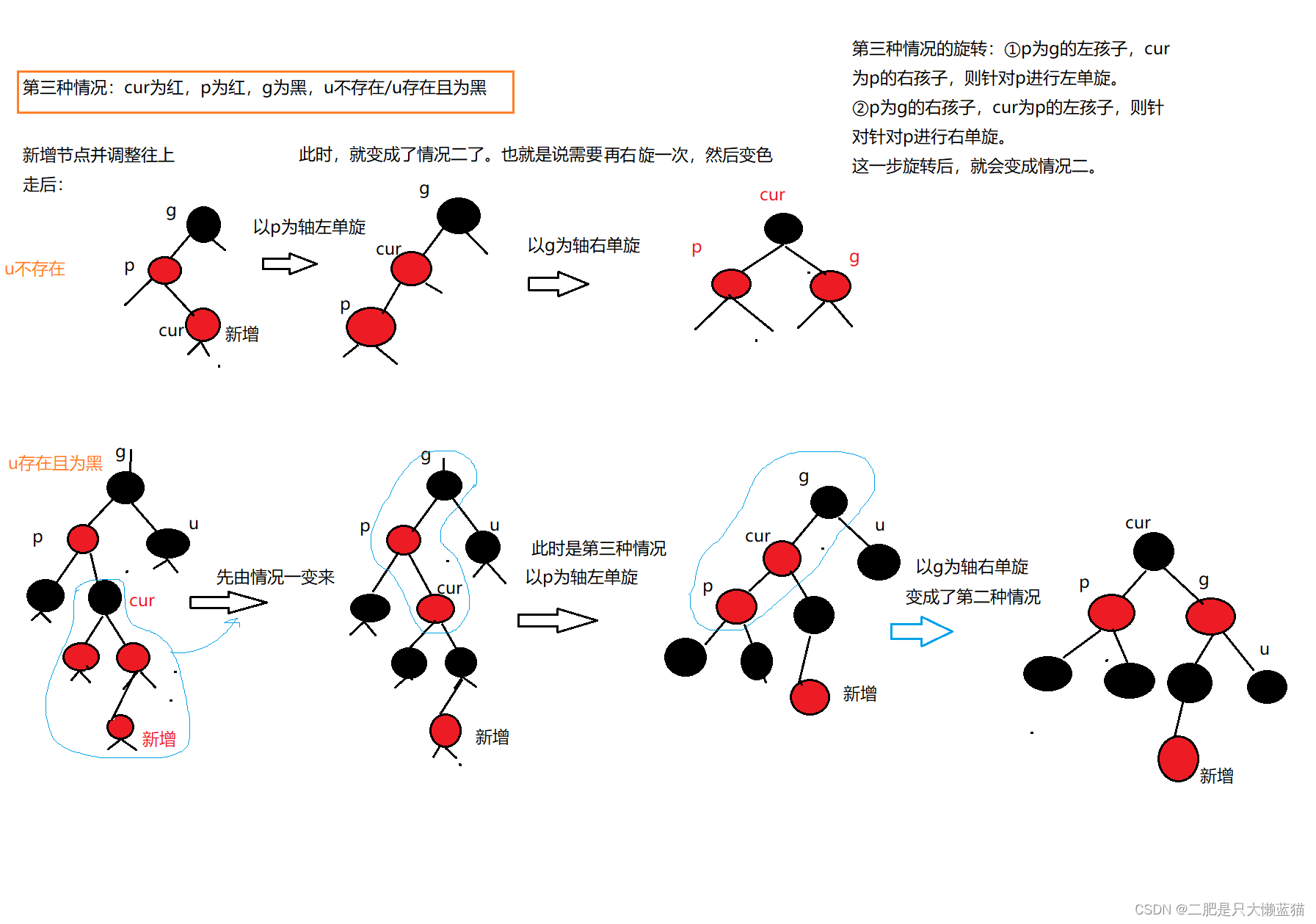
3 熵权法
相对客观的权重计算方法(层次分析法都是自己瞎填)
3.1 原理
指标的变异程度越小,反应的信息越少,对应的权值越低。
一个事件的信息量:I(x) = -ln(p(x))
信息熵:对X可能发生的所有情况的信息量的加权和
∑
\sum
∑[ p(x
i
_{i}
i) * I(x
i
_{i}
i) ]
(当所有p=1/n时值最大为1/n)
3.2 结论
信息熵越大,信息量越小
3.3 计算方式


这里除以ln(n)是为了让最终结果映射到[0,1]
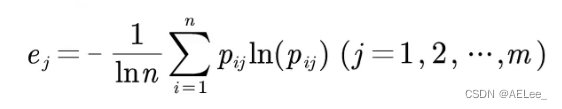
最终用1-e
j
_{j}
j去获得信息效用值,效用值越高,信息越有用。(其中计算出来的概率放在优劣解距离法中)
3.4 反例
比如评定三好学生,一个指标是“是否违纪”,一个指标是“是否缺课”,那么违纪指标可能绝大多数人都是0,而程序会认为这个数据差距过小,权重较低。
4 灰色关联分析
4.1 其他模型坏处(自称)
- 需要大量数据
- 要服从典型概率分布
- 计算量大
- 量化结果和定性分析结果不符
4.2 思想
通过曲线几何形状变化相似程度
4.3 应用1——系统分析
母序列–Y(x
0
_0
0),子序列–X(x
1
_1
1,x
2
_2
2,x
3
_3
3)
1.对变量进行预处理 :每个数据都除以均值
2.计算子序列各个指标与母序列的关联系数:把X分别与Y做差,取一个最小和一个最大值
4.4 应用2——综合评价
刚提到美赛不要用,所以先不看了
5 插值
5.1 拉格朗日插值
在高次拉格朗日的插值中,越高度两点越容易出现龙格现象(波动过大)
解决方案:在左右最近的两个点做二次插值
5.2 高斯插值
见计算方法笔记
6 拟合
6.1 拟合定义
拟合不是像插值一样要契合每一个点,只是和点有比较小的误差即可

平方更好,相比绝对值可以求导,三次方会被正负影响,四次方的异常值影响过大。
6.2 拟合计算
结果:
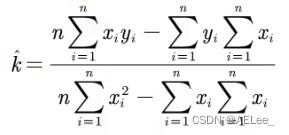
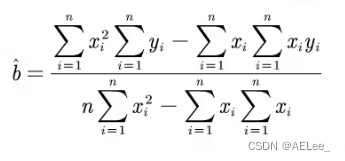
6.3 拟合评价