- 在做数据升维的时候,最常见的手段就是将已知维度进行相乘(或者自乘)来构建新的维度
-
使用 np.concatenate()进行简单的,幂次合并,注意数据合并的方向axis = 1
-
数据可视化时,注意切片,因为数据升维后,多了平方这一维
-
# 4、多项式升维 + 普通线性回归
X = np.concatenate([X,X**2],axis = 1)- 使用 PolynomialFeatures 进行 特征升维
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures() # 使用PolynomialFeatures进行特征升维
poly.fit(X,y)
X = poly.transform(X)- 调整字体大小: plt.rcParams[ 'font.size' ] = 18
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 181.1、多项式回归基本概念
对于多项式回归来说主要是为了扩展线性回归算法来适应更广泛的数据集,比如我们数据集有两个维度 ,那么用多元线性回归公式就是:
,当我们使用二阶多项式升维的时候,数据集就从原来的
扩展成了
。因此多元线性回归就得去多计算三个维度所对应的w值:
。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 1、创建数据,并进行可视化
X = np.linspace(-1,11,num = 100)
y = (X - 5)**2 + 3*X -12 + np.random.randn(100)
X = X.reshape(-1,1)
plt.scatter(X,y)
# 2、创建预测数据
X_test = np.linspace(-2,12,num = 200).reshape(-1,1)
# 3、不进行升维 + 普通线性回归
model_1 = LinearRegression()
model_1.fit(X,y)
y_test_1 = model_1.predict(X_test)
plt.plot(X_test,y_test_1,color = 'red')
# 4、多项式升维 + 普通线性回归
X = np.concatenate([X,X**2],axis = 1)
model_2 = LinearRegression()
model_2.fit(X,y)
# 5、测试数据处理,并预测
X_test = np.concatenate([X_test,X_test**2],axis = 1)
y_test_2 = model_2.predict(X_test)
# 6、数据可视化,切片操作
plt.plot(X_test[:,0],y_test_2,color = 'green')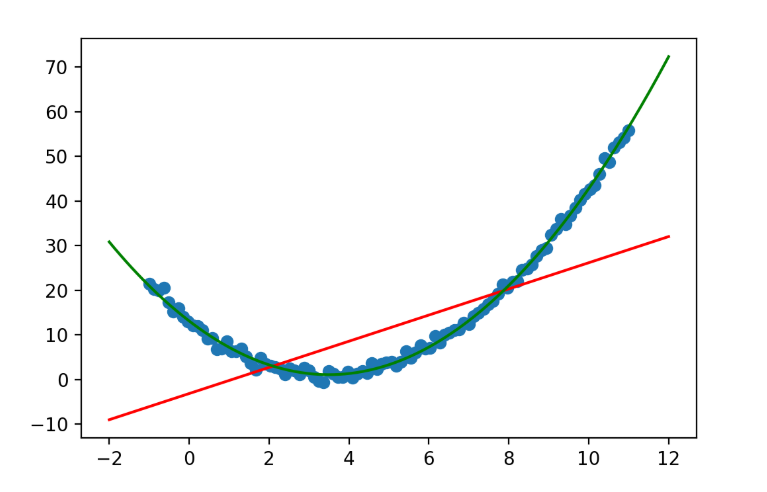
1.2 使用PolynomialFeatures进行特征升维
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.linear_model import SGDRegressor
# 1、创建数据,并进行可视化
X = np.linspace(-1,11,num = 100)
y = (X - 5)**2 + 3*X -12 + np.random.randn(100)
X = X.reshape(-1,1)
plt.scatter(X,y)
# 3、使用PolynomialFeatures进行特征升维
poly = PolynomialFeatures() # 特征升维
poly.fit(X,y)
X = poly.transform(X)
s = StandardScaler() # 归一化
X = s.fit_transform(X)
# 4、训练模型
model = SGDRegressor(penalty='l2',eta0 = 0.01)
model.fit(X,y)
# 2、创建预测数据
X_test = np.linspace(-2,12,num = 200).reshape(-1,1)
X_test = poly.transform(X_test) # 特征升维
X_test_norm = s.transform(X_test) # 归一化
y_test = model.predict(X_test_norm)
plt.plot(X_test[:,1],y_test,color = 'green')1.3 多项式预测
天猫双十一销量与年份的关系是多项式关系!假定,销量和年份之间关系是三次幂关系:
import numpy as np
from sklearn.linear_model import SGDRegressor
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
plt.figure(figsize=(12,9))
# 1、创建数据,年份数据2009 ~ 2019
X = np.arange(2009,2020)
y = np.array([0.5,9.36,52,191,350,571,912,1207,1682,2135,2684])
# 2、年份数据,均值移除,防止某一个特征列数据天然的数值太大而影响结果
X = X - X.mean()
X = X.reshape(-1,1)
# 3、构建多项式特征,3次幂
poly = PolynomialFeatures(degree=3)
X = poly.fit_transform(X)
s = StandardScaler()
X_norm = s.fit_transform(X)
# 4、创建模型
model = SGDRegressor(penalty='l2',eta0 = 0.5,max_iter = 5000)
model.fit(X_norm,y)
# 5、数据预测
X_test = np.linspace(-5,6,100).reshape(-1,1)
X_test = poly.transform(X_test)
X_test_norm = s.transform(X_test)
y_test = model.predict(X_test_norm)
# 6、数据可视化
plt.plot(X_test[:,1],y_test,color = 'green')
plt.bar(X[:,1],y)
plt.bar(6,y_test[-1],color = 'red')
plt.ylim(0,4096)
plt.text(6,y_test[-1] + 100,round(y_test[-1],1),ha = 'center')
_ = plt.xticks(np.arange(-5,7),np.arange(2009,2021))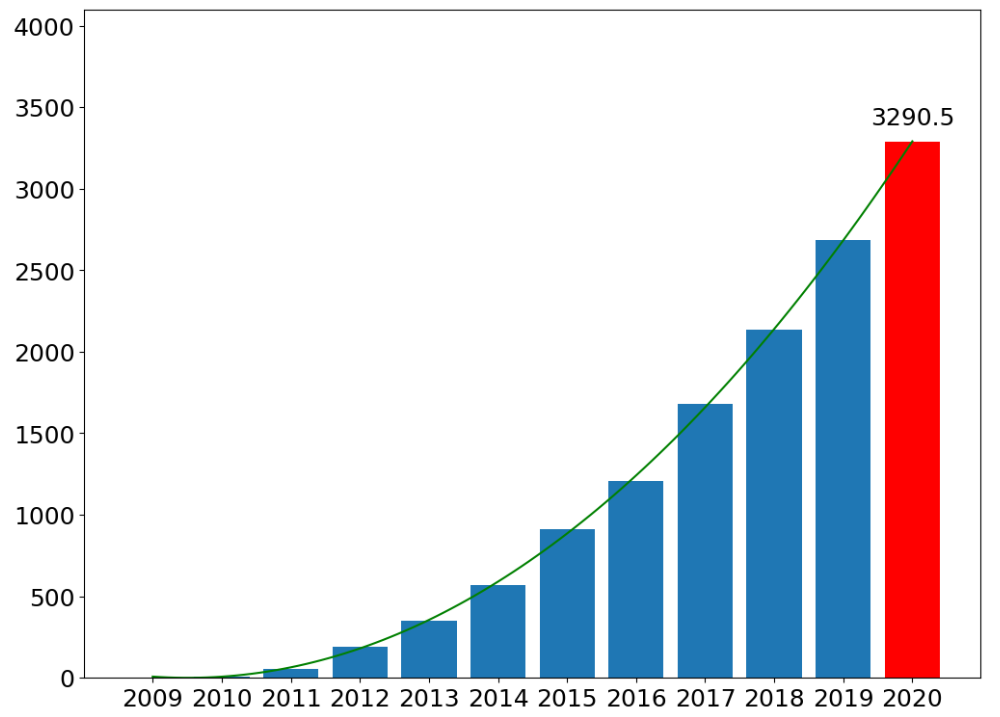






![[K8S]Kubernetes环境检测与API简介](https://img-blog.csdnimg.cn/4cc099c49f32422587a0be7d6814521c.png#pic_center)