WiFi智能插座对于新手接触智能家居产品更加友好，不需要额外购买网关设备

很多智能小配件也给我们得生活带来极大的便捷，智能插座就是其中之一，比如外出忘记关空调，可以拿起手机远程关闭。

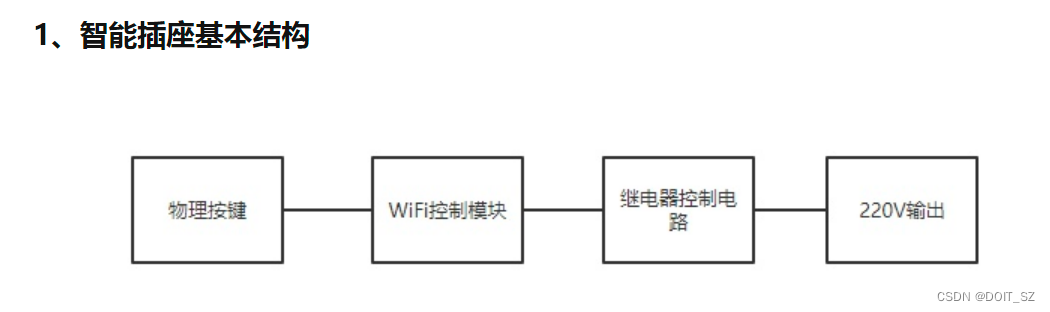
简单说就是：插座可以连接wifi 然后通过手机app进行远程控制、可以语音控制、耗电统计、过载保护、定时开关。

控制指的是 控制开关也就是控制是否通电，进而让普通电器变动“智能”，例如：热水器、电水壶、台灯、加湿器、香薰、空气净化器 等等，想想一下：

当你下班回家想冲个热水澡的时候，只需要打开手机app既可以远程控制，回到家就能洗上热水澡。
当你在家躺在沙发上追着热门电视剧，只需喊一声“xxx帮我烧壶水”，开关就自动打开了，几分钟之后水开了。
当你出门后忘记了断开电源，只需打开手机app，随时随地切断家里的电源，既能省去不必要的耗电也能减少很多安全隐患。
耗电统计指的是可以通过手机app查看到电器的耗电情况，并且如果出现用电过载的情况，可以及时切断电源。

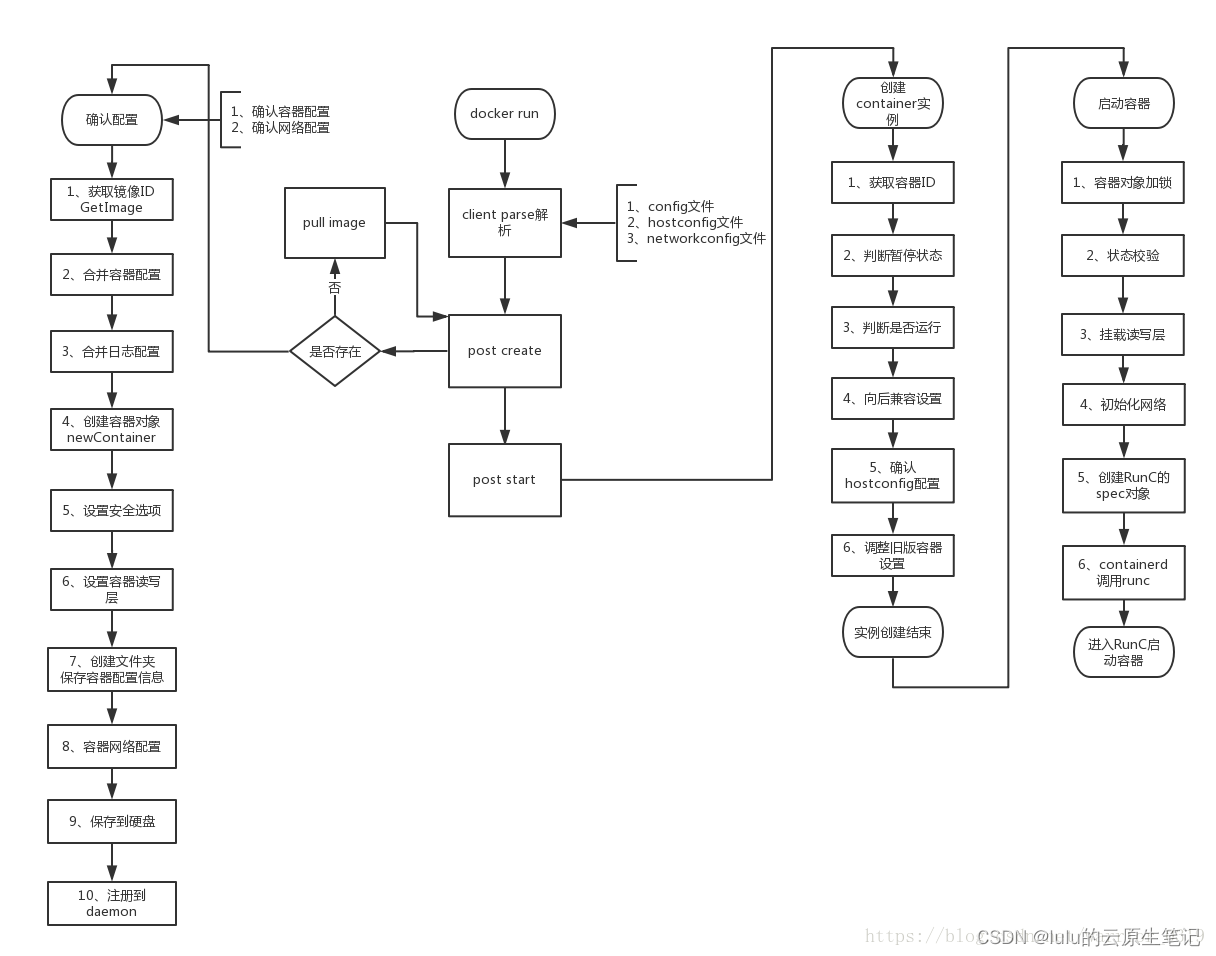
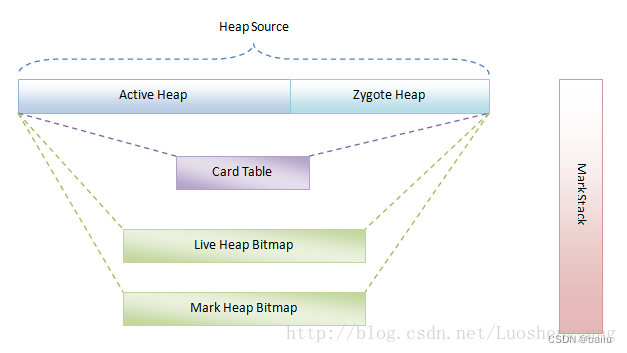
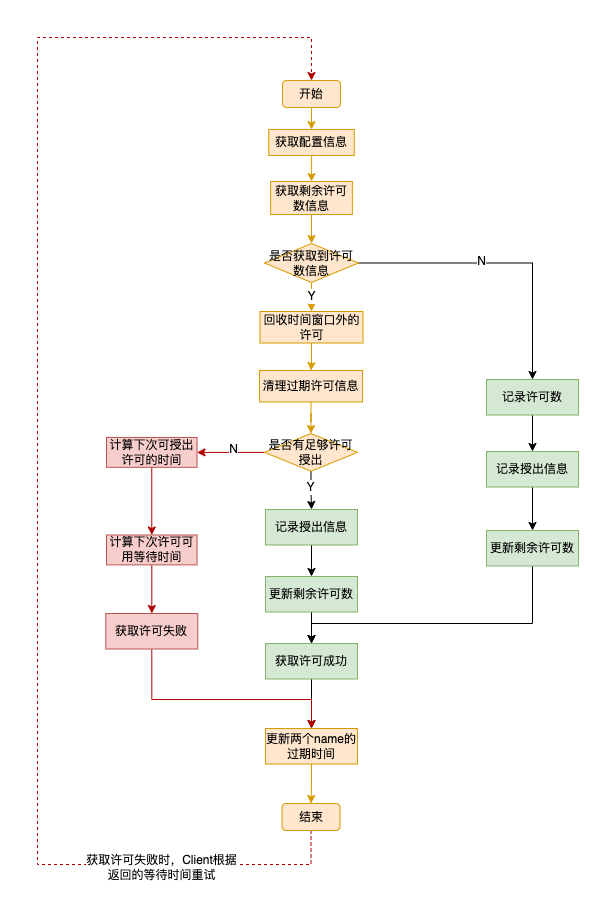
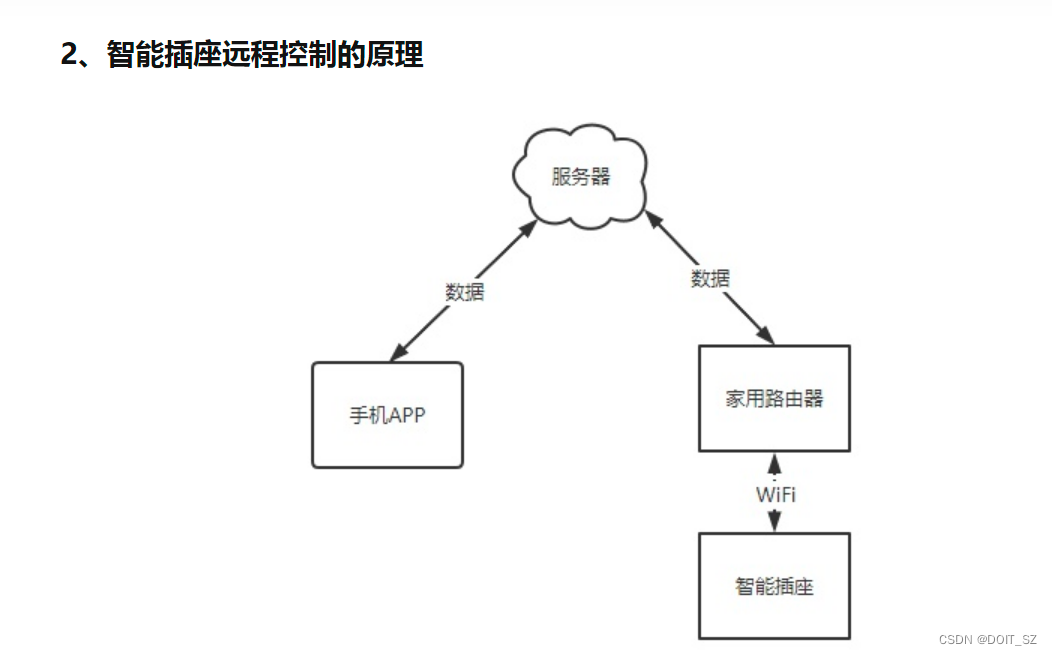
要实现远程控制智能插座，就需要智能插座先连上服务器，这也就是为什么会有在APP内扫描设备，添加设备并且配置WiFi信息的步骤。

当智能插座连上服务器之后，手机打开APP也会连接上服务器，在APP上点击开启开关，就会发送一个指令到服务器，服务器将消息转发给智能插座，智能插座收到指令之后解析出指令的意思，然后把插座打开就完成了一次控制。

3、智能插座作为新手入手的优点
第一，使用方便。智能插座使用上非常简单，只需要将买来的智能插座插到现有的插线板上，将需要控制的电器插到智能插座上就可以了。

第二，性价比高。一个普通WiFi智能插座目前价格一般在40左右，而且一些品牌为了推广时不时还有19.9的。

第三，适用面广。因为使用很方便，理论上只要是传统电器有开关功能的都可以直接接入智能插座，实现自动控制.

4、使用情景介绍
1、如果家里养有鱼，又经常因为外出旅游照顾不了家里的鱼而烦恼，可以考虑将加氧、照明、以及喂食的机器都接入了智能插座，这样就可以直接通过网络就能完成这一系列动作了。

2、如果你担心自己上班时候，小孩偷看电视不好好学习，自己不在家无法控制。那么可以考虑将电视的电源接到了智能插座上，来实现远程查看电视开启关闭情况或者直接远程关掉电视。

(如果觉得智能插座太明显了，可以考虑买了个通断器改装件（就下面那玩意，需要一定动手能力），接在电视机的插线上，把机子涂成了黑色用胶布粘在电视后面，再把按键拆了，免得远程关机后被小孩找到控制器又重新打开电视)

没有计划大规模使用智能家居的话，哪个便宜买哪个。便宜的智能插座体验可以考虑下使用Cozylife的智能插座，这个方案提供商下面的一些设备价格相比其他品牌会有优势点，同时还能支持各大语音平台和Homekit直连。