牛客小白月赛66_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ (nowcoder.com)
冒着期末挂科的风险打了打,缓解了一下网瘾,感觉还行
最近为了期末鸽了很多期的div3,一学期末就手痒想训,感觉再不打人要没了,结果就是预习期末也预习不进去,比赛也没打,这几天不知道在干什么,白白的浪费时间
19号才全部考完,还有8天才训练自由,md,心情非常不愉悦啊

A-先交换
小分类讨论
题意:

思路:
分类讨论即可
#include <bits/stdc++.h>
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
using namespace std;
int n;
int a[mxn];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
int ok=0;
for(int i=2;i<=n;i++){
if(a[i]<a[1]&&a[i]%2==1) ok=1;
}
if(a[1]%2==1) cout<<0<<'\n';
else if(ok&&a[1]%2==0) cout<<1<<'\n';
else cout<<-1<<'\n';
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;cin>>__;
while(__--)solve();return 0;
}B-再交换
构造+小分类讨论
题意:

思路:
构造题,交换的两个数的位置一定是特殊的,考虑i=j的情况进行交换,这样就是小分类讨论
注意特判的情况,当两个串串完全相同时,不代表无解,还可以交换别的数来满足条件
在a数组找到第一个不是最小值的数,在b数组找到最后一个最小值,进行交换即可
#include <bits/stdc++.h>
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
using namespace std;
int n;
string s,t;
void solve(){
s.clear(),t.clear();
cin>>n;
cin>>s>>t;
s=" "+s;
t=" "+t;
int mi=1e9;
for(int i=1;i<=n;i++){
mi=min(mi,s[i]-'a'+1ll);
if(s[i]==t[i]) continue;
else if(s[i]<t[i]){
if(i==n) cout<<1<<" "<<1<<'\n';
else cout<<n<<" "<<n<<'\n';
return;
}else{
cout<<i<<" "<<i<<'\n';
return;
}
}
int ansi;
for(int i=n;i>=1;i--){
if(t[i]-'a'+1==mi){
ansi=i;
break;
}
}
int p=1;
while(s[p]-'a'+1==mi) p++;
if(p!=1) cout<<p<<" "<<p-1<<'\n';
else{
cout<<1<<" "<<ansi<<'\n';
}
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;cin>>__;
while(__--)solve();return 0;
}C-空洞骑士
构造+大(小)分类讨论

思路:
首先这题是让我们构造位置,那位置肯定是特殊的
考虑一个0到1e9的数轴,中间的金币是随机分配的,我们只需要记录第一个金币和最后一个金币的位置,然后去考虑起点s的位置
三种情况:
s=0
s=中间某个位置
s=1e9

画个图就可以发现,s为中间那个位置的贡献一定比另外两种小
如果s在中间,贡献差不多就是1.5个p_end-p_start,但是如果s=0或1e9,贡献显然>2*(p_end-p_start),所以第二种情况可以直接淘汰了
那么讨论另外两种情况,然后算一算贡献就行
当s=0时,t取1e9或1,两种情况算贡献取大的那个
当s=1e9,t=1e9-1或1,两种情况算贡献取大的那个
我自己在写的时候把中间的那种情况也算进去了,但是不影响ac
#include <bits/stdc++.h>
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
const int end_p=1000000000;
using namespace std;
int m;
int p[mxn];
void solve(){
cin>>m;
int p_mx=-1e9,p_mi=1e9;
for(int i=1;i<=m;i++){
cin>>p[i];
p_mx=max(p_mx,p[i]);
p_mi=min(p_mi,p[i]);
}
sort(p+1,p+1+m);
int mx=-1e9,ansi;
for(int i=1;i<=m;i++){
if(mx<min(p_mx-p[i],p[i]-p_mi)){
mx=min(p_mx-p[i],p[i]-p_mi);
ansi=p[i];
}
}
int a1=max(p_mx+p_mx-1ll,(long long)1e9);
int a3=((1e9-1)-p_mi>p_mi?(1e9-1)-p_mi:p_mi)+1e9-p_mi;
int a2=min(p_mx-ansi,ansi-p_mi)+p_mx-p_mi+(p_mx-ansi<ansi-p_mi?p_mi:1e9-p_mx);
int ans_a=max(max(a1,a2),a3);
//cout<<a3<<'\n';
if(ans_a==a1){
if(p_mx-1>1e9-p_mx) cout<<0<<" "<<1<<'\n';
else cout<<0<<" "<<end_p<<'\n';
}else if(ans_a==a2){
if(p_mx-ansi<ansi-p_mi) cout<<ansi<<" "<<0<<'\n';
else cout<<ansi<<" "<<end_p<<'\n';
}else{
if(1e9-1-p_mi>p_mi) cout<<end_p<<" "<<end_p-1<<'\n';
else cout<<end_p<<" "<<0<<'\n';
}
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;//cin>>__;
while(__--)solve();return 0;
}D-障碍
枚举+前缀和
题意:

思路:
这道题只需要注意到x的取值范围,那么就很好做了,关键是比赛的时候还注意不到
L最大取2e5,那么x最大就是500,如果超过500那么答案就会是负的
遇到小数据,我们考虑暴力枚举就好了
去枚举拿掉多少个障碍,然后去维护最大的答案值
#include <bits/stdc++.h>
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
using namespace std;
int n,m,x;
int a[mxn];
void solve(){
cin>>n>>m;
for(int i=1;i<=m;i++) cin>>a[i];
a[0]=0,a[m+1]=n;
int ans=-1e9;
for(int len=0;len<=500;len++){
for(int l=0;l<=m;l++){
int r=l+len+1;
ans=max(ans,a[r]-a[l]-len*len);
}
}
cout<<ans<<'\n';
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;//cin>>__;
while(__--)solve();return 0;
}E生成树与路径
图论+构造
题意:

思路:
关于图论的构造还没怎么写过
这道题的构造条件是:
1.n个点,m条边
2.最小生成树的大小是最短路大小
3.特殊条件是边是个排列
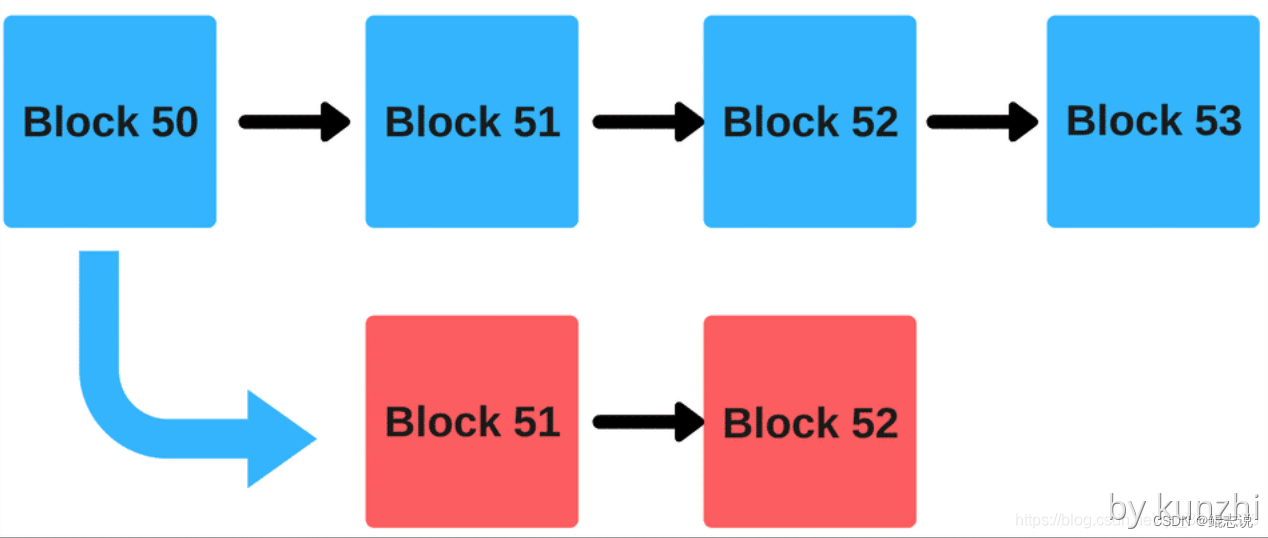
对于第一个条件,考虑构造1到n的一条链,并边长是1-n-1,这样就满足了第一个条件
然后因为要m条边,所以我们要继续连边,但是在连边的过程中要保证第一个条件
我们考虑这样连边:

#include <bits/stdc++.h>
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
using namespace std;
int n,m,u,v,idx=0;
void solve(){
idx=0;
cin>>n>>m;
for(int len=2;len<=n;len++){
for(int l=1;l+len-1<=n;l++){
int r=l+len-1;
cout<<l<<" "<<r<<" "<<++idx<<'\n';
if(idx==m) return;
}
}
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;cin>>__;
while(__--)solve();return 0;
}F-球球大作战
贪心+反证法(?)+二分
题意:


思路:
我们要求的是,对于一个球,是否存在一种方法使得这个球作为最终的胜利者
首先是一个结论:其他n-1个球自相残杀之后,再和这个球去碰撞,这样这个球是最大值
证明:
反证法,如果该球和其他任意一个球撞击:
若这个球比较小,直接输掉
若这个球比较大,权值变成(a1+a2)/2,且a2<a1,所以权值不会变大,证毕
那么,其他n-1个球该怎么去撞可以最小化这n-1个球碰撞后的值呢,求出最好情况就可以看是否存在解法了
另一个结论就是:
这n-1个球从小到大排好序之后最大值和次大值碰撞可以使n-1个值碰撞之后的值最小
(另外n-1个球是无序的,所以可以考虑排序)
证明:
反证法:
考虑三个球,直接去计算它们的贡献:

注意到a1的贡献除了2,a2和a3的贡献除了4
因此先撞大的球会使贡献变小
证毕
如果我们就这样去枚举球,复杂度是O(n2)的,肯定T
但是对于两个球,如果权值较小的那个球都有解的可能性,那权值较大的一定有解
因为,权值较小的球,其他n-1个球碰撞之后的权值一定比除了那个权值较大的球其他n-1个球碰撞之后的权值来的大
所以满足了单调性,直接去二分刚好有解的权值的下标就好了,前提是数组排好序
#include <bits/stdc++.h>
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
using namespace std;
int n,ans;
int a[mxn],b[mxn];
bool check(int x){
int ans=a[n];
for(int i=n-1;i>=1;i--){
if(i==x) continue;
ans+=a[i];
ans/=2;
}
return ans<=a[x];
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
sort(a+1,a+1+n);
int l=1,r=n;
while(l<=r){
int mid=l+r>>1;
if(check(mid)){
ans=mid;
r=mid-1;
}else l=mid+1;
}
//cout<<ans<<'\n';
int s=a[ans];
for(int i=1;i<=n;i++){
if(b[i]>=s) cout<<1;
else cout<<0;
}
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int __=1;//cin>>__;
while(__--)solve();return 0;
}