题目描述

原题链接：416. 分割等和子集

解题思路

题目要求是划分出两个相等的集合，那么这两个相等的集合相加，一定等于偶数并且为总集合的二分之一，若总集合求和后不为偶数，则一定不可以划分，直接返回false即可。

因为本题的每个数只能用一次，本题可转化为01背包问题，背包容量为原集合求和的二分之一，选择nums中的数，进行装取，当装入的容量达到求和的二分之一时，说明可以划分集合。其中，原集合中的数=物品体积=物品价值，找到某种装入方式价值最大，也就是找到某种方式，在确定体积下装入最多。

动态规划五步曲：

（1）dp[j]的含义： 在背包体积j的条件下，可装入的物品体积最大之和。

（2）递推公式： dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])

（3）dp数组初始化： dp[0] = 0

（4）遍历顺序： 因采用滚动数组，因此先物品，再背包，内层按背包容量从大到小的顺序遍历。

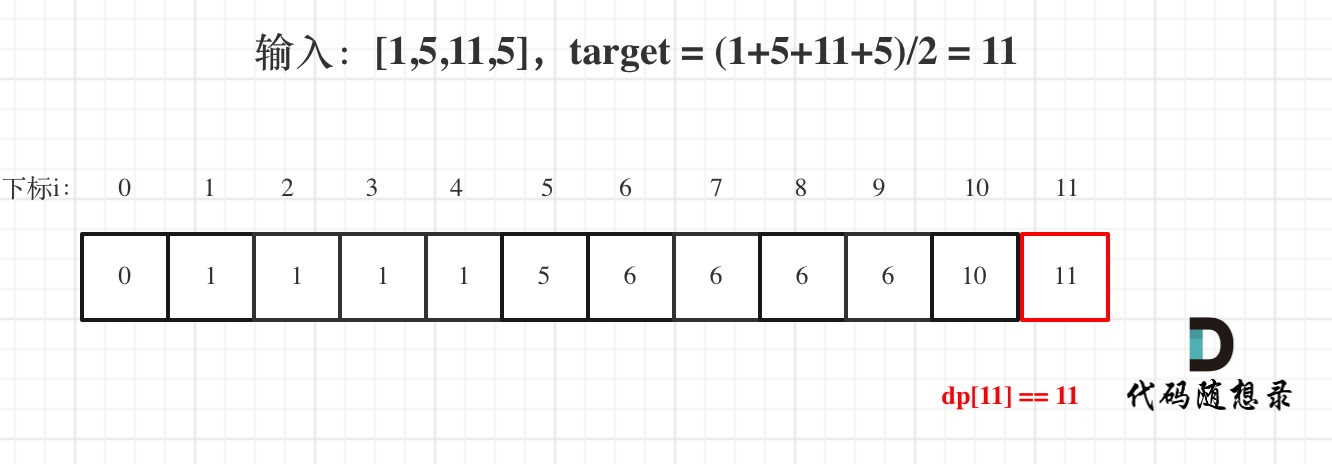
（5）举例：

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sumNums = 0;
        for(int i = 0; i < nums.size(); i++)     sumNums += nums[i];
        if(sumNums % 2 != 0)            return false;
        sumNums /= 2;

        int dp[10001] = {0};
        int n = nums.size();        
        for(int i = 0; i < n; i++) {
            for(int j = sumNums; j >= nums[i]; j--) {
                dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
            }
        }

        return dp[sumNums] == sumNums;
    }
};

二维数组

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sumNums = 0;
        for(int i = 0; i < nums.size(); i++)     sumNums += nums[i];
        if(sumNums % 2 != 0)                     return false;
        sumNums /= 2;

        int n = nums.size();
        int dp[201][10001] = {0};
        for(int i = 1; i < n; i++) {
            for(int j = 1; j <= sumNums; j++) {
                if(nums[i - 1] > j)     
                    dp[i][j] = dp[i - 1][j];
                else 
                    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i - 1]] + nums[i - 1]);
            }
        }

        return dp[n - 1][sumNums] == sumNums;
    }
};

参考文章：416. 分割等和子集