文章目录
- 一、前言
- 二、概述
- 三、打家劫舍第一晚
- 四、打家劫舍第二晚
- 五、打家劫舍第三晚......
一、前言
大家好久不见,正如标题所示,今天我不打算聊一些枯燥的算法理论,我们来聊一聊程序员有多厉害!
注意!!!:本文诣在讲解
动态规划里的打家劫舍问题,无任何不良导向!!!
二、概述
一个月黑风高的夜晚~,你回到了村庄,你是一名资深的程序员,你工作认真努力,但苦于老板压迫,生活常常捉襟见肘,于是你的内心萌生了罪恶的想法!你准备在这个村庄里打劫!
三、打家劫舍第一晚
第一天晚上,你来到了一个村庄,你计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的 唯一制约因素 就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。而你想要在一夜之内偷取最高金额。
聪明的你知道如果报警器响起会发生什么,所以你打算运用你作为程序员的聪明才智来帮助你完成打劫!
于是你简单分析了街道房屋的构成,并将其抽象为了数组,简单分析报警器就可以知道,只要不偷相邻元素的钱就不会触发报警!
看过前两期动态规划的你,立马就意识到这是一个动态规划问题,没看过也没关心,你稍微动了一下脑筋,梳理出来以下思路:
✔️dp数组
在第0间~第 i 间房子内,要遵守相邻房间不能偷的原则,偷得最大金额!这个i是会变化的,所以你决定使用一个dp数组来保存你能偷的最大金额
dp[i] 表示:
第0间房子~第i间房子内按照规则能偷取的最大金额
✔️状态转移
片刻后,你决定要偷一共i间房子的钱,并打听好了每间房子有多少钱可以偷(value)。
于是你想,若要求dp[i],无非就两种情况:
1. 偷第i家
2.不偷第i家
1.那如果偷第i家,根据规则,相邻房间不能再偷,所以第i-1家就要避开
- dp[i] = dp[i-2] + value[i]
2.那如果不偷第i家,根据规则,i-1家就不需要避开
- dp[i] = dp[i-1];
而我们只需要在上述两种情况下选金额较大的即是dp[i]的值!因此状态转移方程即为:
dp[i] = max(dp[i-1],dp[i-2] + value[i]);
到这里,你不禁感叹不愧是程序员,轻松做到了其他人做不到的事情!
✔️初始化
推导出上述动态转移方程,你就自然而然想到前两个元素要初始化,那初始化为什么好呢,回顾了一下dp数组的含义,你顺利完成了初始化
- dp[0] = value[0];
- dp[1] = max(value[0],value[1]);
简单解释一下:
你只有一间房子可选,你就说你选不选吧~
不能都选,但总得选个贵的吧~
✨参考代码
class Solution {
public:
int rob(vector<int>& nums) {
if(nums.size() == 0) return 0;
if(nums.size() == 1) return nums[0];
vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]);
for(int i = 2;i<nums.size();i++){
dp[i] = max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[nums.size()-1];
}
};
四、打家劫舍第二晚
昨晚你作案非常顺利,成功拿到了最大金额,为了避免被别人发现,第二天你来到了一个新的村庄,村庄结构变成了一个环形!,你同样不能偷相邻房间的钱!!
你分析了一下,发现这个村庄的构成与上个村庄非常相似,只是首尾相连了而已,那这样的变化会带来什么问题呢?
很简单,无非就是选择了第一家就不能偷最后一家,选择了最后一家,就一定不能偷第一家。
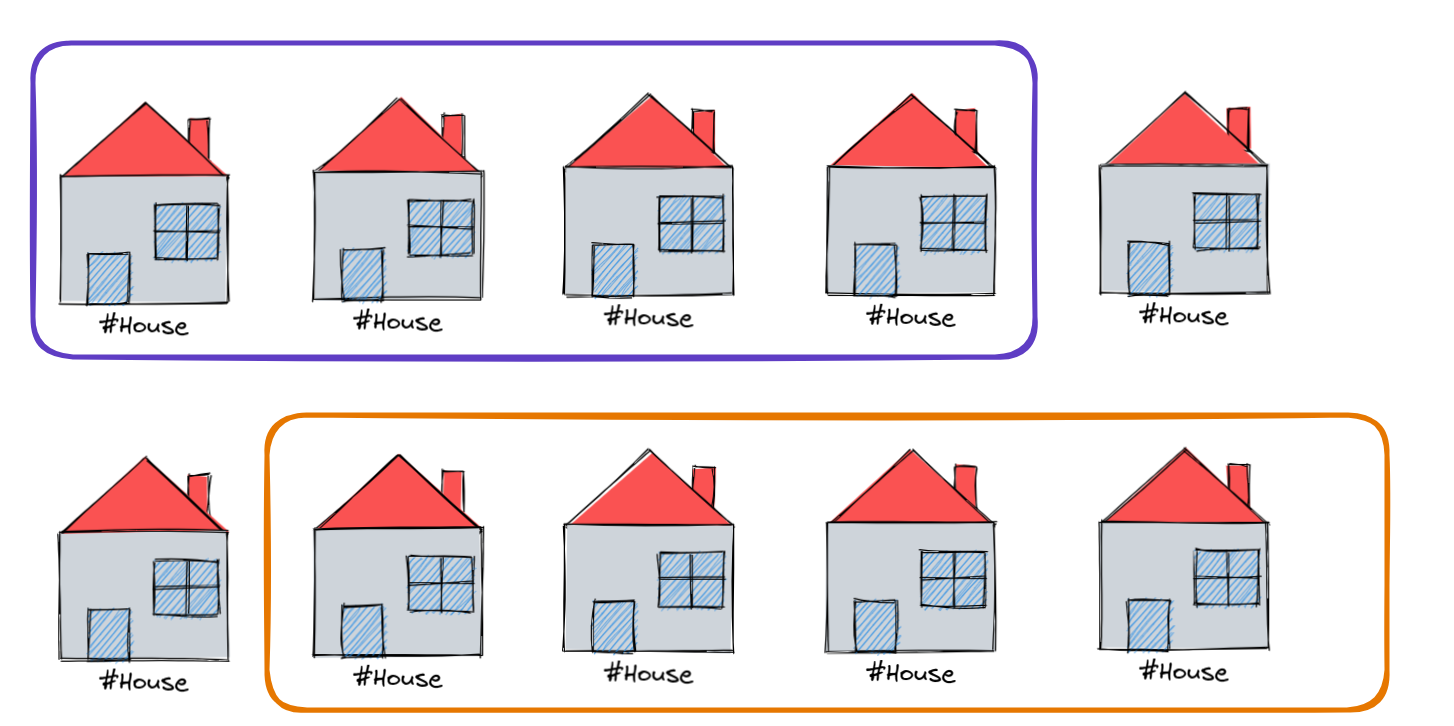 这样,你成功将一个环形结构拆成了两个队列结构,只要分别求出他们,选择最大的那个即可!
这样,你成功将一个环形结构拆成了两个队列结构,只要分别求出他们,选择最大的那个即可!
那分别求每一个队列的过程,和你第一天的情况完全一致,你也很轻松的偷到了最多的钱。
class Solution {
public:
//抽象第一天的过程
int robRange(vector<int>& nums,int start,int end)
{
if (end == start) return nums[start];
vector<int> dp(nums.size());
dp[start] = nums[start];
dp[start+1] = max(nums[start],nums[start+1]);
for(int i = start+2;i<=end;i++)
{
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[end];
}
int rob(vector<int>& nums) {
if (nums.size() == 0) return 0;
if (nums.size() == 1) return nums[0];
int result1 = robRange(nums, 0, nums.size() - 2); // 第一个队列
int result2 = robRange(nums, 1, nums.size() - 1); //第二个队列
return max(result1, result2);//选择最大的那个啦!!!
}
};
五、打家劫舍第三晚…
鉴于你前两晚作案都非常顺利,不出所料,第三天晚上你再次来到了一个村庄,这次村庄结构竟然变成了二叉树!!作为程序员的你马上就兴奋了起来,那么你到底能不能顺利偷得第三个村庄,拿到最多钱呢。
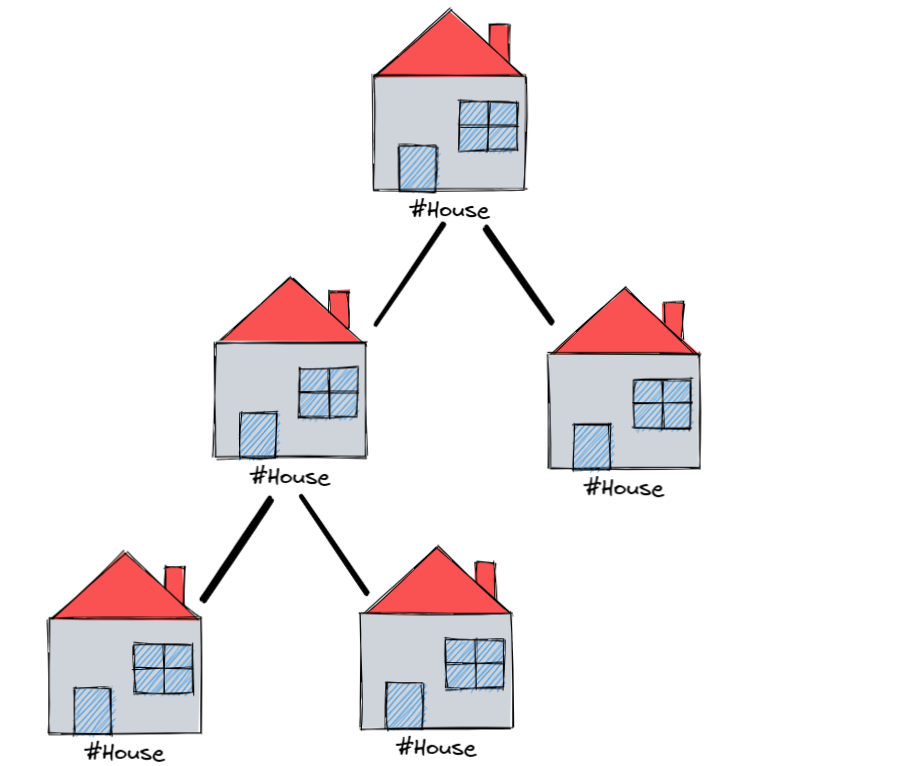
欲知后事如何,且听下节课分解!!!大家可以先自己想一想,下次我们先学会二叉树的基本知识,再来偷最后的村子!
如果你感觉本篇文章对你有所帮助,可以点赞 + 收藏 +关注 支持一下学者哦~ 我们下次再见~