前言
这是一个经典的图论问题了
最近复习离散的时候又恰好看到了,发现自己以前的解法似乎有点bug
然后开始出反例卡自己,结果发现卡不掉?
然后再好好想了想,发现这个看起来有问题的做法可能确实没问题。
注意:欧拉路、欧拉回路、欧拉图、半欧拉图四个概念的区别
Fleury算法
这是离散数学书上的经典求解欧拉路的算法之一

非常好理解,只不过如何快速判断正在删边的图的桥实现起来比较麻烦,如果没有好的数据结构的支持,时间复杂度将会多乘一个(n+m),所以正常情况下我们不用Fleury算法来求解欧拉路
逐步插入回路法
这个方法离散数学书上并没有细讲,而仅仅只用一句话带过了

我们可以先来看看定理15.1(欧拉回路的判定定理)的充分性证明
充分性:G是无向连通图且没有奇度顶点=>G中存在欧拉回路(G是欧拉图)


大致意思就是
(1)G中必定存在圈
书中用可以证明四个字带过了
这个可以用极大路径法证明
因为δ(G)≥2,那么找一条图中的极大路径,路径的端点一定存在一条边连向路径中的点(否则路径就可以继续延长,与极大路径矛盾),这样就会构成一个圈。
(2)删掉这个圈后,剩下的连通分支都是欧拉图(由归纳法假设可得)
(3)以这个大圈上的一点为出发点,走到与删掉后的连通分支上的点后,先把子欧拉回路走完,然后再继续向前走。
证明过程如此,那么如何将其转换为算法呢?
可以利用归纳法的思想,对图G进行分治,先任意找圈,然后删圈,判连通性,在各个连通分支递归,答案返回后再一起整合……反正写起来巨麻烦,而且没必要
另一种可能的解法
为什么说是可能呢,因为我也感觉自己不能很严谨的证明这个做法的正确性
先上代码:

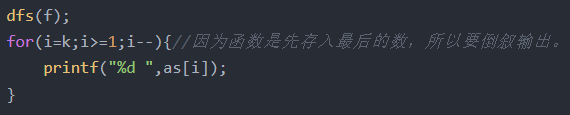
这里省略了对图进行(半)欧拉图判定的过程以及选起始点的过程
只保留了计算的主体部分
可以说是非常诡异,初看时觉得有点道理,细想之后发现完全不对劲,但是它却AC了
于是我开始举反例
8
0 1 1 1 1 0 1 1
1 0 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 1 1 0 0
1 0 0 1 0 1 0 0
0 0 0 1 1 0 0 0
1 0 0 0 0 0 0 1
1 0 0 0 0 0 1 0
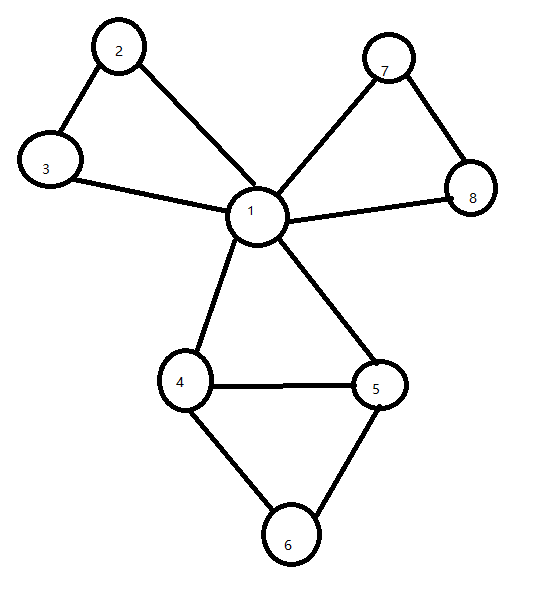

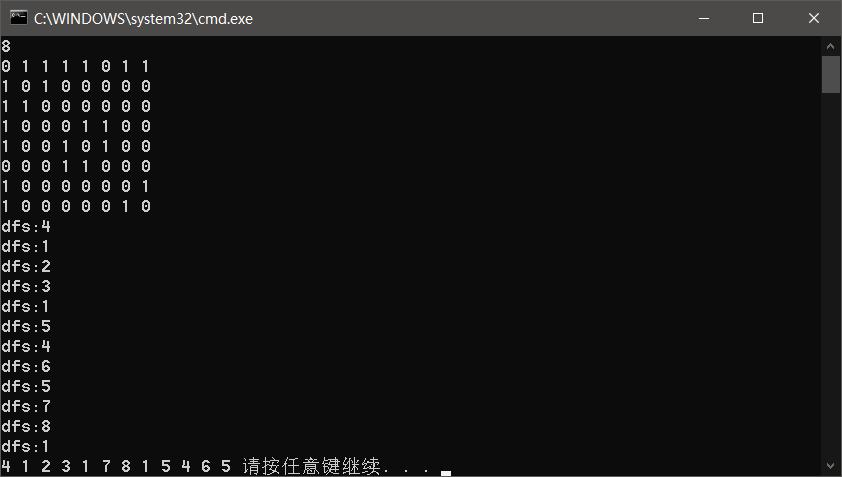
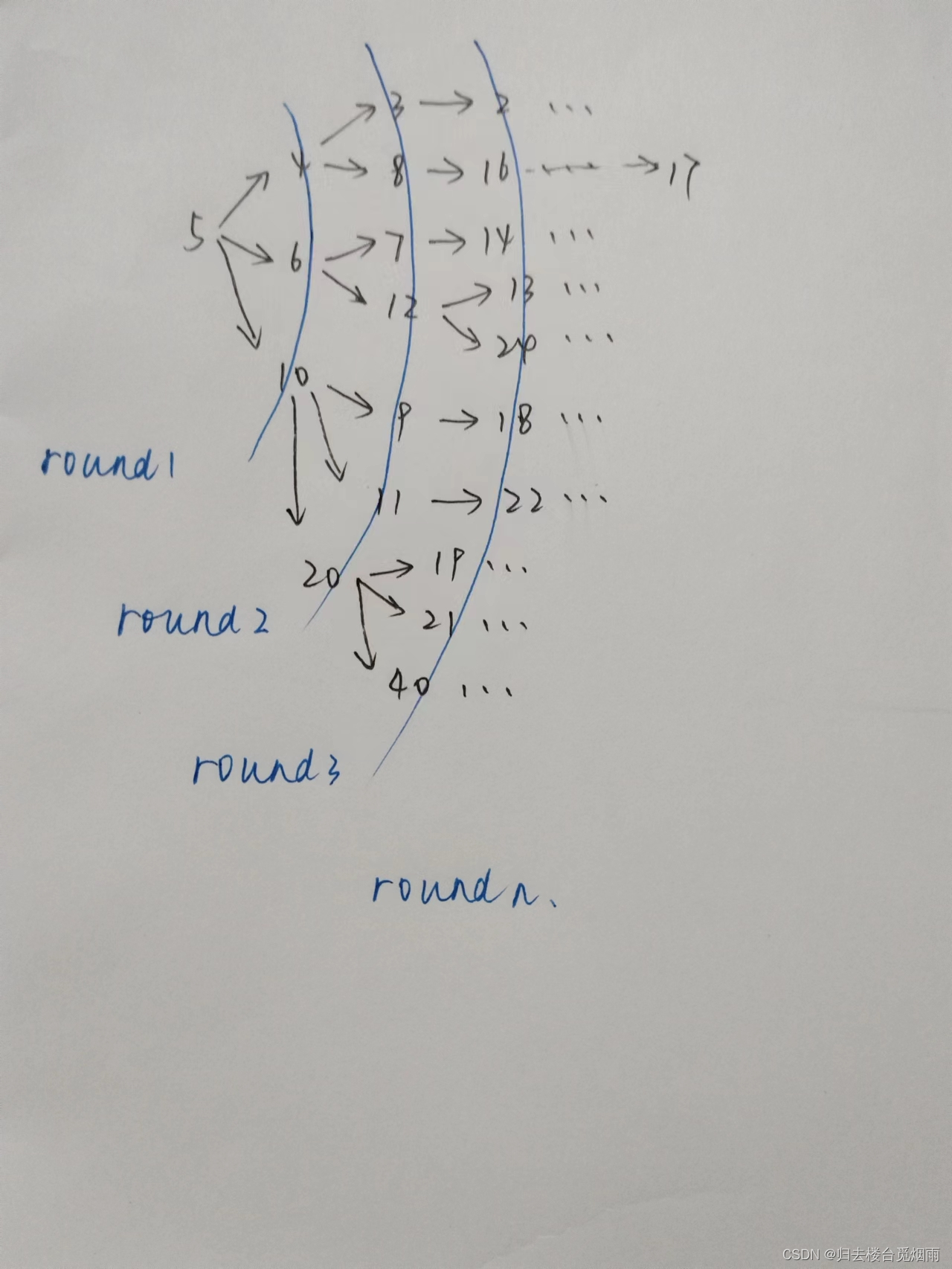
可以发现程序的dfs过程确实时错误的,但是最后输出的结果确实对的
关键就是在于保存答案的位置和输出答案的顺序。
dfs输出的位置是入栈的位置,而保存答案的位置是出栈的位置
Fluery算法告诉我们,我们在做一笔画时出错的原因是,在不必要的时候先走了桥,导致没办法走回来
也就是说,我们应该最后走桥
虽然这个做法中我们并不能保证我们最后走的是桥
但是我们知道
先走桥的肯定会先出栈(因为会走不通,导致退栈回溯)
所以过桥的答案一定会被先统计到
而且最后又是倒序输出,这样就间接地保证了过桥之后的答案最后输出
也就间接地保证了这个做法的正确性。
这个做法是OI中比较普遍的欧拉路求解算法,然而我的这个证明是很不严谨的,希望有识之士可以补充更加严谨的证明。
完结撒花~~~~( •̀ ω •́ )y