电子技术——MOS差分输入对

差分输入系统因其极高的共模抑制能力,差分输入几乎是是构建所有通用模拟IC的基本前级输入,也是现代信号传输理论的基础。本节我们讲解MOS差分输入对。
MOS差分输入对
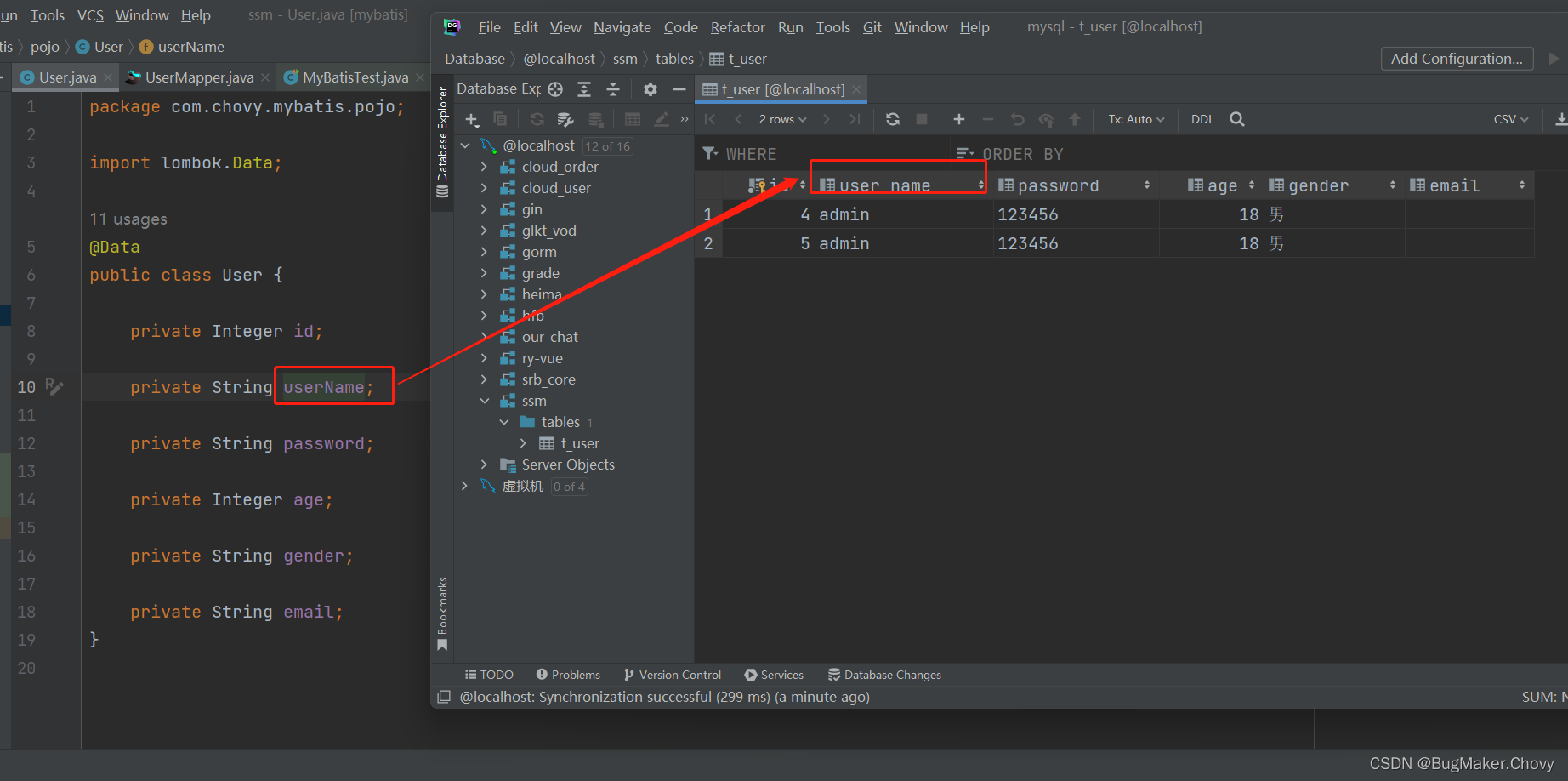
下图展示了MOS差分输入对的基本原理图:
一个MOS差分输入对是由两个完全匹配的MOS管
Q
1
Q_1
Q1 和
Q
2
Q_2
Q2 组成,并且他们的源极相连,共用一个电流源偏置
I
I
I ,这通常是我们在上一章学习的MOS电流镜,但是在这里我们先假设这是一个理想的电流源并且有无限大的阻抗。尽管我们在漏极使用电阻
R
D
R_D
RD 但是在实际情况下是通过主动负载实现的,只是我们为了说明差分输入对的功能而使用简单的电阻负载,无论使用那种阻抗,唯一一点需要保证的是每一个MOS都处在饱和区。
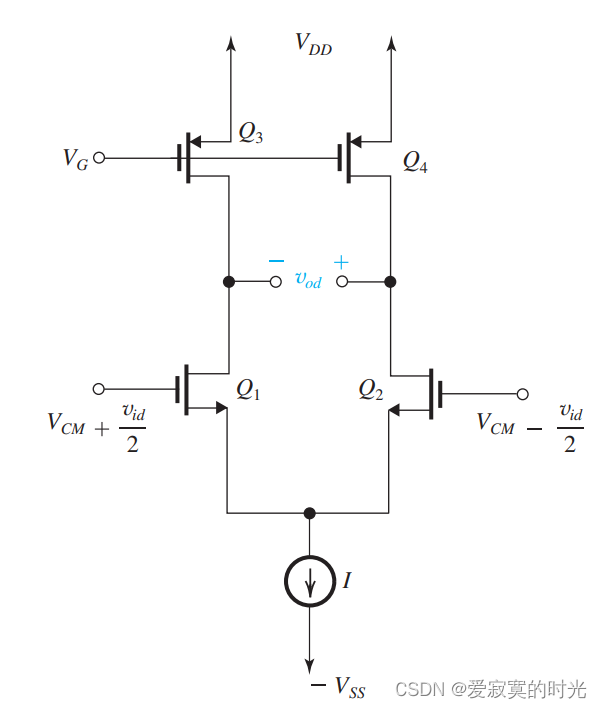
MOS差分输入对有两个输入端 v G 1 v_{G1} vG1 和 v G 2 v_{G2} vG2 ,以及两个输出端 v D 1 v_{D1} vD1 和 v D 2 v_{D2} vD2 。
共模输入
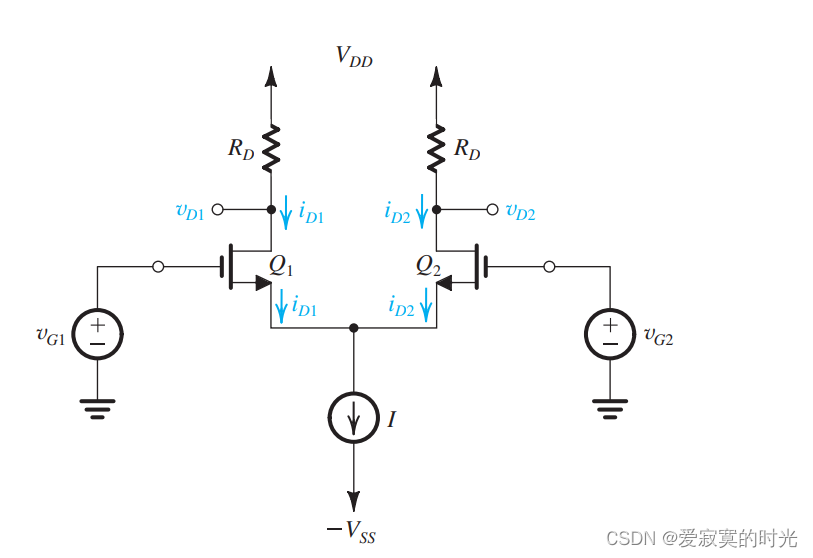
为了说明差分输入对如何工作,我们首先讨论在共模输入下的情况。也就是说,两个输入的电压信号源是完全相等的,如下图:
此时两个输入端的信号源均为
v
G
1
=
v
G
2
=
V
C
M
v_{G1} = v_{G2} = V_{CM}
vG1=vG2=VCM ,因为
V
C
M
V_{CM}
VCM 同时出现在两个输入端,因此我们称其为 共模信号电压 。因为电路完全对称,电流
I
I
I 被两个MOS平分,即
i
D
1
=
i
D
2
=
I
/
2
i_{D1} = i_{D2} = I/2
iD1=iD2=I/2 。源极电压可以表示为:
V S = V C M − V G S V_S = V_{CM} - V_{GS} VS=VCM−VGS
因为MOS处在饱和区,有饱和电流:
I 2 = 1 2 k n ′ W L ( V G S − V t ) 2 \frac{I}{2} = \frac{1}{2} k_n' \frac{W}{L} (V_{GS} - V_t)^2 2I=21kn′LW(VGS−Vt)2
因此 V O V V_{OV} VOV 为:
V O V = I / k n ′ ( W / L ) V_{OV} = \sqrt{I/k_n'(W/L)} VOV=I/kn′(W/L)
这导出漏极输出电压:
v D 1 = v D 2 = V D D − I 2 R D v_{D1} = v_{D2} = V_{DD} - \frac{I}{2}R_D vD1=vD2=VDD−2IRD
因此,输出端电压的差值为零。现在我们调整 V C M V_{CM} VCM 的大小,只要保证MOS都处在饱和区,那么电路就是完全对称的,输出端电压的差值始终为零,差分输入对不会对共模信号产生相应,或是说是抑制共模信号。
MOS差分输入对一个重要的属性是 输入共模信号范围 。这是令MOS差分输入对正确工作的 V C M V_{CM} VCM 区间。以上面的电路图为例, V C M V_{CM} VCM 的最大值是MOS管在饱和区的边界点:
V C M m a x = V t + V D D − I 2 R D V_{CMmax} = V_t + V_{DD} - \frac{I}{2} R_D VCMmax=Vt+VDD−2IRD
最小值是MOS允许流过电流为 I I I 的边界点:
V C M m i n = − V S S + V C S + V t + V O V V_{CMmin} = -V_{SS} + V_{CS} + V_t + V_{OV} VCMmin=−VSS+VCS+Vt+VOV
这里 V C S V_{CS} VCS 是电流源 I I I 允许的最小压降。
差分输入
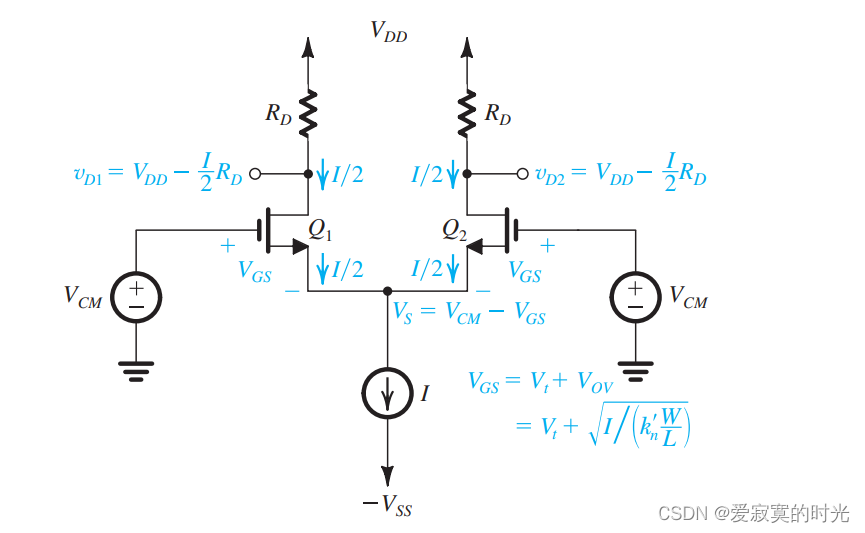
现在我们将 Q 2 Q_2 Q2 的栅极置地,在 Q 1 Q_1 Q1 的栅极应用电压 v i d v_{id} vid ,如下图所示:
因为
v
i
d
=
v
G
S
1
−
v
G
S
2
v_{id} = v_{GS1} - v_{GS2}
vid=vGS1−vGS2 若
v
i
d
v_{id}
vid 是正数,那么
v
G
S
1
>
v
G
S
2
v_{GS1} > v_{GS2}
vGS1>vGS2 进而
i
D
1
>
i
D
2
i_{D1} > i_{D2}
iD1>iD2 ,最终使得
v
D
2
−
v
D
1
v_{D2} - v_{D1}
vD2−vD1 是正的,另外一方面,若
v
i
d
v_{id}
vid 是负数,最终将导致
v
D
2
−
v
D
1
v_{D2} - v_{D1}
vD2−vD1 是负的。
我们发现,若输入端电压存在差值,那么MOS差分输入对就会对其进行响应,体现在输出端的差值上。我们称输入存在差值的信号称为 差分信号 。
MOS差分输入对一个重要的属性是 输入差分信号范围 。这是令MOS差分输入对正确工作的 v i d v_{id} vid 区间。
首先存在正边界,当电流 I I I 完全从 Q 1 Q_1 Q1 流过,此时 i D 1 = I i_{D1} = I iD1=I ,而且对于 Q 2 Q_2 Q2 来说,此时处于截止区的边界 v G S 2 = V t v_{GS2} = V_t vGS2=Vt 即 v S = − V t v_S = -V_t vS=−Vt 。则:
I = 1 2 ( k n ′ W L ) ( v G S 1 − V t ) 2 I = \frac{1}{2} (k_n' \frac{W}{L}) (v_{GS1} - V_t)^2 I=21(kn′LW)(vGS1−Vt)2
这导出:
v G S 1 = V t + 2 I / k n ′ ( W / L ) = V t + 2 V O V v_{GS1} = V_t + \sqrt{2I/k_n'(W/L)} = V_t + \sqrt{2}V_{OV} vGS1=Vt+2I/kn′(W/L)=Vt+2VOV
这里 V O V V_{OV} VOV 是当漏极电流为 I / 2 I/2 I/2 的时候的MOS过驱动电压。则此时:
v i d m a x = v G S 1 + v S = 2 V O V v_{idmax} = v_{GS1} + v_S = \sqrt{2}V_{OV} vidmax=vGS1+vS=2VOV
若 v i d > 2 V O V v_{id} > \sqrt{2}V_{OV} vid>2VOV 则 I D 1 I_{D1} ID1 继续保持 I I I ,为了保证 v G S 1 = V t + 2 V O V v_{GS1} = V_t + \sqrt{2}V_{OV} vGS1=Vt+2VOV 则 v S v_S vS 同步增加,因此 Q 2 Q_2 Q2 处于截止状态。对于负边界也同样,因此 v i d v_{id} vid 的范围在:
− 2 V O V ≤ v i d ≤ 2 V O V -\sqrt{2}V_{OV} \le v_{id} \le \sqrt{2}V_{OV} −2VOV≤vid≤2VOV
大信号模型
接下来,我们对MOS差分输入对的大信号模型进行定量分析,我们仍然假设MOS都是完全匹配的且忽略厄尔利电压。我们只讨论大信号模型下漏极电流对差分信号的响应,因此漏极接入什么都无所谓的,我们使用下图的一般情况:
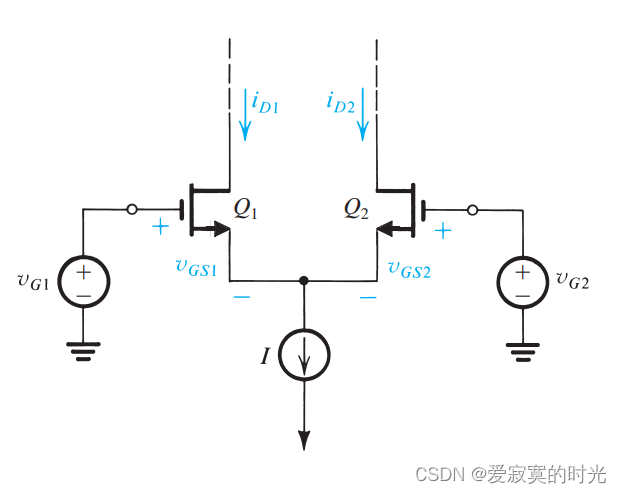
在开始之前,我们先提前写出漏极电流表达式:
i D 1 = 1 2 k n ′ W L ( v G S 1 − V t ) 2 i_{D1} = \frac{1}{2} k_n' \frac{W}{L} (v_{GS1} - V_t)^2 iD1=21kn′LW(vGS1−Vt)2
i D 2 = 1 2 k n ′ W L ( v G S 2 − V t ) 2 i_{D2} = \frac{1}{2} k_n' \frac{W}{L} (v_{GS2} - V_t)^2 iD2=21kn′LW(vGS2−Vt)2
对两边同时开方得到:
i D 1 = 1 2 k n ′ W L ( v G S 1 − V t ) \sqrt{i_{D1}} = \sqrt{\frac{1}{2} k_n' \frac{W}{L}}(v_{GS1} - V_t) iD1=21kn′LW(vGS1−Vt)
i D 2 = 1 2 k n ′ W L ( v G S 2 − V t ) \sqrt{i_{D2}} = \sqrt{\frac{1}{2} k_n' \frac{W}{L}}(v_{GS2} - V_t) iD2=21kn′LW(vGS2−Vt)
作差得到:
i D 1 − i D 2 = 1 2 k n ′ W L ( v G S 1 − v G S 2 ) \sqrt{i_{D1}} - \sqrt{i_{D2}} = \sqrt{\frac{1}{2} k_n' \frac{W}{L}}(v_{GS1} - v_{GS2}) iD1−iD2=21kn′LW(vGS1−vGS2)
带入 v G S 1 − v G S 2 = v G 1 − v G 2 = v i d v_{GS1} - v_{GS2} = v_{G1} - v_{G2} = v_{id} vGS1−vGS2=vG1−vG2=vid 得到:
i D 1 − i D 2 = 1 2 k n ′ W L v i d \sqrt{i_{D1}} - \sqrt{i_{D2}} = \sqrt{\frac{1}{2} k_n' \frac{W}{L}}v_{id} iD1−iD2=21kn′LWvid
又因为总电流恒定:
i D 1 + i D 2 = I i_{D1} + i_{D2} = I iD1+iD2=I
这是一个二元方程,解得:
i D 1 = I 2 + k n ′ W L I ( v i d 2 ) 1 − ( v i d / 2 ) 2 I / k n ′ W L i_{D1} = \frac{I}{2} + \sqrt{k_n' \frac{W}{L}I}(\frac{v_{id}}{2}) \sqrt{1 - \frac{(v_{id}/2)^2}{I/k_n'\frac{W}{L}}} iD1=2I+kn′LWI(2vid)1−I/kn′LW(vid/2)2
i D 2 = I 2 − k n ′ W L I ( v i d 2 ) 1 − ( v i d / 2 ) 2 I / k n ′ W L i_{D2} = \frac{I}{2} - \sqrt{k_n' \frac{W}{L}I}(\frac{v_{id}}{2}) \sqrt{1 - \frac{(v_{id}/2)^2}{I/k_n'\frac{W}{L}}} iD2=2I−kn′LWI(2vid)1−I/kn′LW(vid/2)2
当 v i d = 0 v_{id} = 0 vid=0 的时候,存在:
i D 1 = i D 1 = I / 2 i_{D1} = i_{D1} = I/2 iD1=iD1=I/2
对应:
v G S 1 = v G S 2 = V G S v_{GS1} = v_{GS2} = V_{GS} vGS1=vGS2=VGS
这里:
I / 2 = 1 2 k n ′ W L ( V G S − V t ) 2 = 1 2 k n ′ W L V O V 2 I/2 = \frac{1}{2}k_n'\frac{W}{L}(V_{GS} - V_t)^2 = \frac{1}{2}k_n'\frac{W}{L}V_{OV}^2 I/2=21kn′LW(VGS−Vt)2=21kn′LWVOV2
我们将 I / V O V 2 I/V_{OV}^2 I/VOV2 带入到 k n ′ ( W / L ) k_n'(W/L) kn′(W/L) 中:
i D 1 = I 2 + ( I V O V ) ( v i d 2 ) 1 − ( v i d / 2 V O V ) 2 i_{D1} = \frac{I}{2} + (\frac{I}{V_{OV}})(\frac{v_{id}}{2}) \sqrt{1 - (\frac{v_{id}/2}{V_{OV}})^2} iD1=2I+(VOVI)(2vid)1−(VOVvid/2)2
i D 2 = I 2 − ( I V O V ) ( v i d 2 ) 1 − ( v i d / 2 V O V ) 2 i_{D2} = \frac{I}{2} - (\frac{I}{V_{OV}})(\frac{v_{id}}{2}) \sqrt{1 - (\frac{v_{id}/2}{V_{OV}})^2} iD2=2I−(VOVI)(2vid)1−(VOVvid/2)2
这个两个表达式描述了漏极电流对差分信号的响应。为了方便,我们绘制 i D / I i_D/I iD/I 和 v i d / V O V v_{id}/V_{OV} vid/VOV 的归一化图像:
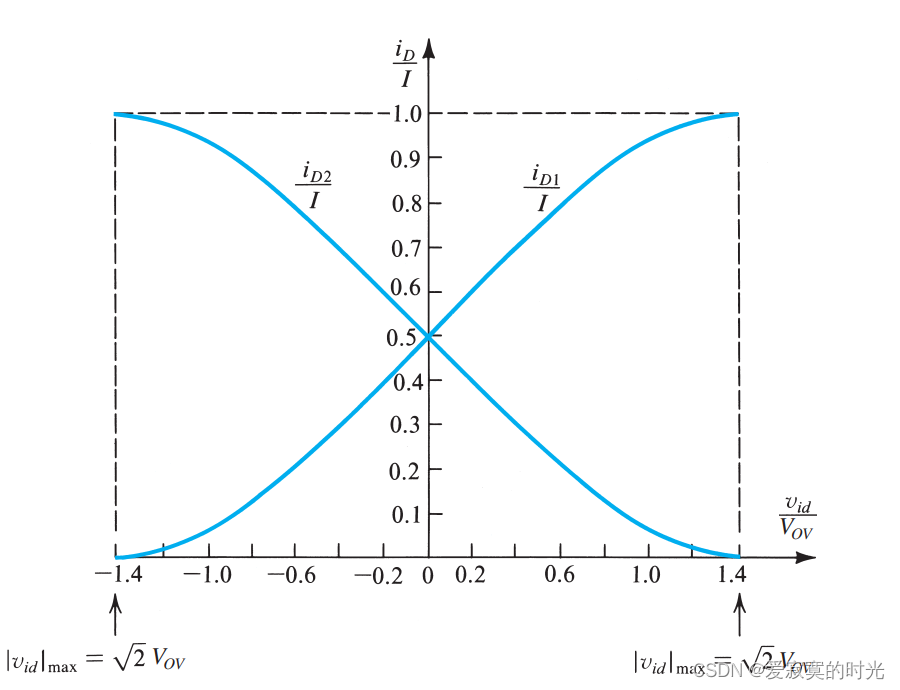
注意到,当 v i d = 0 v_{id} = 0 vid=0 的时候,两个漏极电流均为 I / 2 I/2 I/2 ;让 v i d v_{id} vid 向正方向移动,此时 i D 1 i_{D1} iD1 增大而 i D 2 i_{D2} iD2 减小,并且保证总和始终为 I I I 。当 v i d v_{id} vid 达到 2 V O V \sqrt{2}V_{OV} 2VOV 的时候, I I I 完全流入 Q 1 Q_1 Q1 。对于负数区域来说也同样。
观察到漏极电流对差分信号做出的响应并不是线性的,因为存在一个包含 v i d 2 v_{id}^2 vid2 的项,为了获得一个线性区域,我们保证 ( v i d / 2 ) ≪ V O V (v_{id}/2) \ll V_{OV} (vid/2)≪VOV ,这就是小信号估计的条件,可以近似得到:
i D 1 ≃ I 2 + ( I V O V ) ( v i d 2 ) i_{D1} \simeq \frac{I}{2} + (\frac{I}{V_{OV}})(\frac{v_{id}}{2}) iD1≃2I+(VOVI)(2vid)
i D 2 ≃ I 2 − ( I V O V ) ( v i d 2 ) i_{D2} \simeq \frac{I}{2} - (\frac{I}{V_{OV}})(\frac{v_{id}}{2}) iD2≃2I−(VOVI)(2vid)
我们令电流差值:
i d = ( I V O V ) ( v i d 2 ) i_d = (\frac{I}{V_{OV}})(\frac{v_{id}}{2}) id=(VOVI)(2vid)
此时 i D 1 i_{D1} iD1 增加 i d i_d id 而 i D 2 i_{D2} iD2 减少 i d i_d id 。之前我们在MOSFET章节学到过,当MOS的漏极偏置电流为 I I I 的时候,此时互导系数为 g m = 2 I V O V g_m = \frac{2I}{V_{OV}} gm=VOV2I 。在这里我们同样见到了,这里的每个MOS的互导系数为 I V O V \frac{I}{V_{OV}} VOVI 因为每个漏极偏置电流为 I 2 \frac{I}{2} 2I 。为什么电压是 v i d 2 \frac{v_{id}}{2} 2vid ?仅仅是因为让 v g s 1 = v i d / 2 v_{gs1} = v_{id}/2 vgs1=vid/2 以及 v g s 2 = − v i d / 2 v_{gs2} = -v_{id}/2 vgs2=−vid/2 才能让 i D 1 i_{D1} iD1 增加 i d i_d id 而 i D 2 i_{D2} iD2 减少 i d i_d id 。
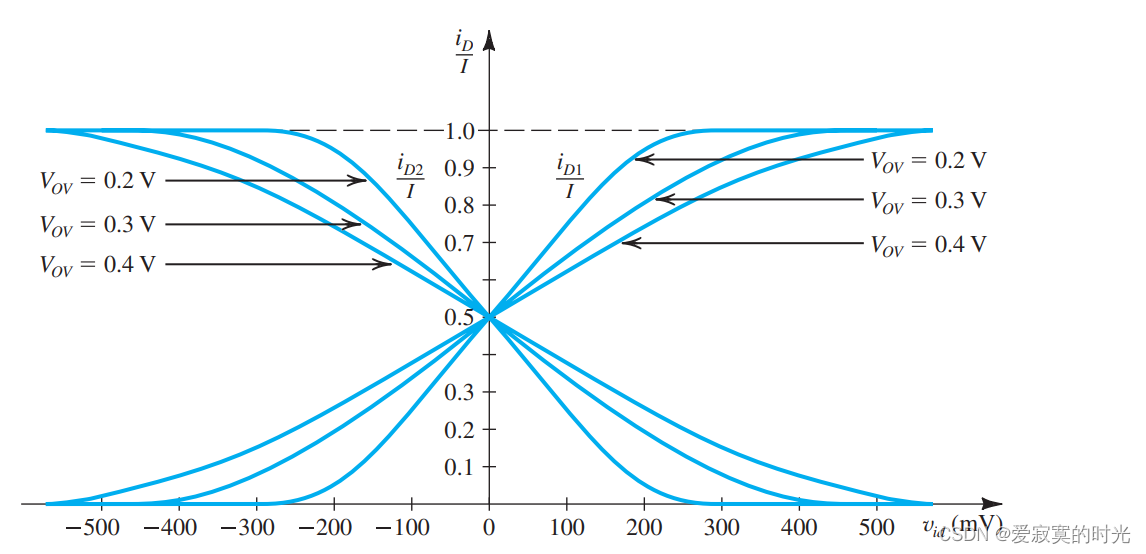
现在我们回到一开始的那个式子,让 V O V V_{OV} VOV 越大则响应越线性。通过使用更小的 W / L W/L W/L 的MOS管可以做到。代价就是也同时减小了 g m g_m gm 减小了增益,虽然可以通过增大偏置 I I I 来弥补增益的损失,但是这却增加了放大器的实际功耗,这通常被IC设计所限制。下图展示了不同 V O V V_{OV} VOV 的响应曲线:
小信号模型
接下来我们讨论MOS差分输入对的小信号模型。
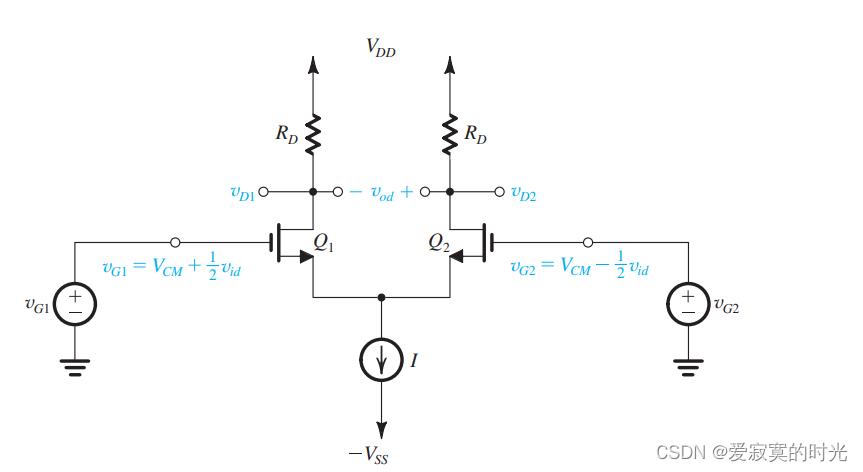
下图展示了MOS差分输入对的输入电压:
v
G
1
=
V
C
M
+
1
2
v
i
d
v_{G1} = V_{CM} + \frac{1}{2}v_{id}
vG1=VCM+21vid
v G 2 = V C M − 1 2 v i d v_{G2} = V_{CM} - \frac{1}{2}v_{id} vG2=VCM−21vid
其中 V C M V_{CM} VCM 是共模信号输入,可以看着是输入的DC电压。一般情况下, V C M V_{CM} VCM 是电源电压的中值,例如当使用完全互补的双电源方案,此时 V C M = 0 V_{CM} = 0 VCM=0 。
对于差分信号 v i d v_{id} vid 使用 互补 (或 平衡 )行为输入到MOS差分输入对。也就是说, v G 1 v_{G1} vG1 增加 v i d / 2 v_{id}/2 vid/2 而 v G 2 v_{G2} vG2 减少 v i d / 2 v_{id}/2 vid/2 。这是大部分的输入配置,因为MOS差分输入对的输入一般是另一个MOS差分输入对的输出。有时,也有使用 单端输入 的情况,例如我们一开始讨论的那个电路。不同的输入方式造成了电流需求上的一些微妙的差异。
而对于输出,也同样有两个方式。第一种是使用一个输出端和地之间的电压,这种方式也称为 单端输出 ,此时 v o 1 v_{o1} vo1 (或 v o 2 v_{o2} vo2 )对地的电压是DC偏置 ( V D D − I 2 R D ) (V_{DD} - \frac{I}{2}R_D) (VDD−2IRD) 以及输出信号电压。第二种是使用一个输出端和另一个输出端的电压,称为 差分输出 ,此时输出电压 v o d v_{od} vod 没有DC分量,完全是由信号分量组成。
为了分析MOS差分输入对对小信号 v i d v_{id} vid 的响应,我们移除所有DC分量,如图:
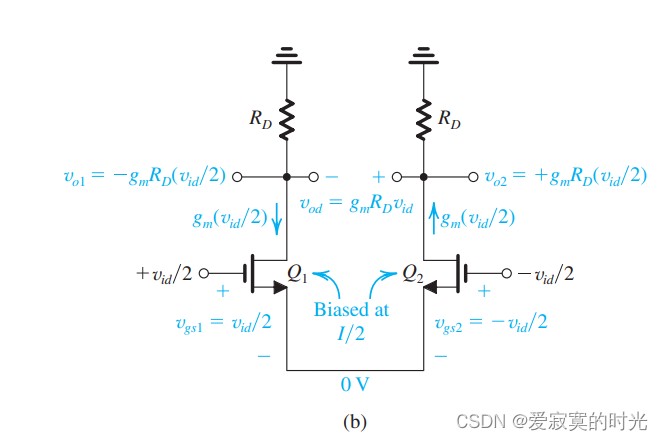
由于电路的对称性,我们知道源极的信号电压一定是
v
i
d
/
2
v_{id}/2
vid/2 和
−
v
i
d
/
2
-v_{id}/2
−vid/2 ,也就是0V,这形成了一个 虚拟AC地 。此时
v
g
s
1
=
v
i
d
/
2
v_{gs1} = v_{id}/2
vgs1=vid/2 而
v
g
s
2
=
−
v
i
d
/
2
v_{gs2} = -v_{id}/2
vgs2=−vid/2 ,所以
Q
1
Q_1
Q1 增加电流
g
m
(
v
i
d
/
2
)
g_m(v_{id}/2)
gm(vid/2) 而
Q
2
Q_2
Q2 减少电流
g
m
(
v
i
d
/
2
)
g_m(v_{id}/2)
gm(vid/2) ,这里
g
m
g_m
gm 是MOS的互导系数:
g m = 2 I D V O V = I V O V g_m = \frac{2I_D}{V_{OV}} = \frac{I}{V_{OV}} gm=VOV2ID=VOVI
为了进一步说明,我们使用等效T模型:
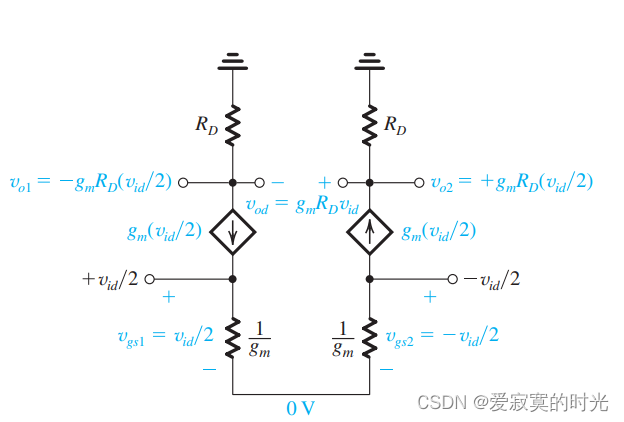
另外,我们发现,AC信号地是自动形成的,不需要使用大容值的旁路电容,这也是MOS差分输入对的优点之一。
则输出电压可以表示为:
v o 1 = − g m v i d 2 R D v_{o1} = -g_m\frac{v_{id}}{2}R_D vo1=−gm2vidRD
v o 2 = + g m v i d 2 R D v_{o2} = +g_m\frac{v_{id}}{2}R_D vo2=+gm2vidRD
若是单端输出,则增益为:
∣ A v ∣ ≡ v o v i d = 1 2 g m R D |A_v| \equiv \frac{v_{o}}{v_{id}} = \frac{1}{2}g_mR_D ∣Av∣≡vidvo=21gmRD
若是差分输出,则增益为:
A d ≡ v o d v i d = v o 2 − v o 1 v i d = g m R D A_d \equiv \frac{v_{od}}{v_{id}} = \frac{v_{o2} - v_{o1}}{v_{id}} = g_mR_D Ad≡vidvod=vidvo2−vo1=gmRD
可以看出差分输出的增益是单端输出的两倍。然而,单端输出应用于其他应用,我们之后会讨论。
我们在分析互补输入的时候,等效于分析一个半电路,如图:
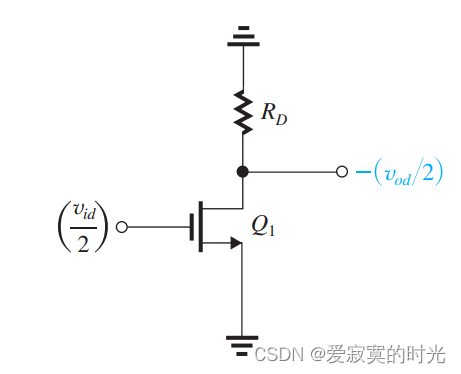
若考虑厄尔利电压,则:
A d = g m ( R D ∣ ∣ r o ) A_d = g_m(R_D || r_o) Ad=gm(RD∣∣ro)
电流源负载的差分放大器
为了获得更大的增益,我们可以将 R D R_D RD 换成主动负载,如图:
此时使用半电路法分析:
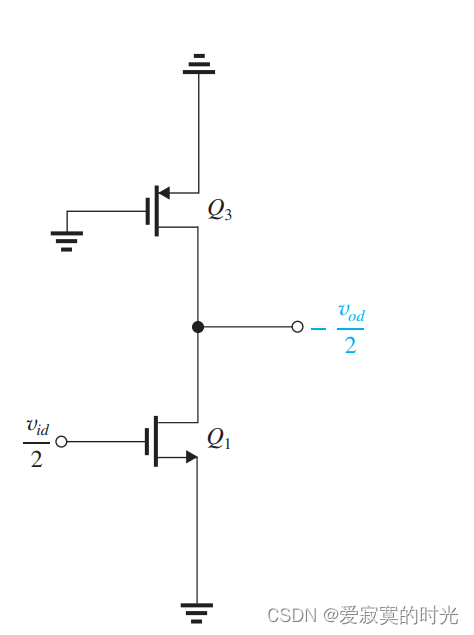
得到增益为:
A d = g m 1 ( r o 1 ∣ ∣ r r o 3 ) A_d = g_{m1}(r_{o1} || r_{r_{o3}}) Ad=gm1(ro1∣∣rro3)
共源共栅差分放大器
若想进一步提升MOS差分输入对的增益,可以使用共源共栅差分放大器,如图:
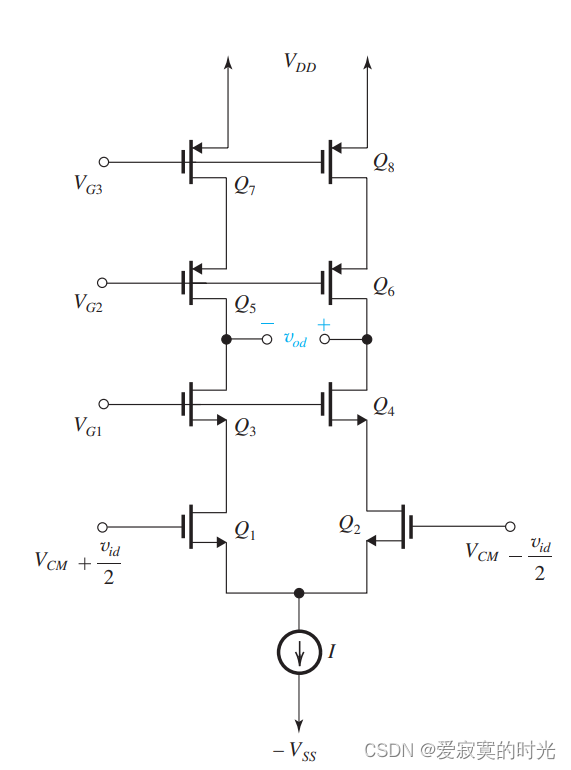
使用半电路分析:
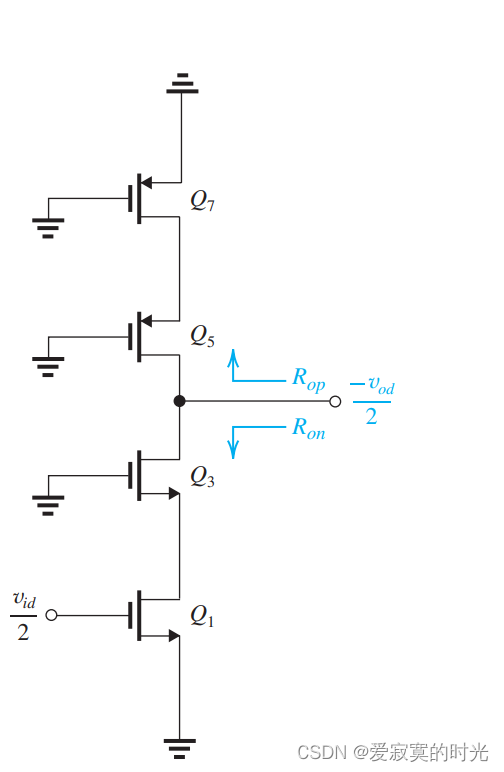
得到:
A d = g m 1 ( R o n ∣ ∣ R o p ) A_d = g_{m1}(R_{on} || R_{op}) Ad=gm1(Ron∣∣Rop)
这里:
R o n = ( g m 3 r o 3 ) r o 1 R_{on} = (g_{m3}r_{o3})r_{o1} Ron=(gm3ro3)ro1
R o p = ( g m 5 r o 5 ) r o 7 R_{op} = (g_{m5}r_{o5})r_{o7} Rop=(gm5ro5)ro7