深度学习实战（11）：使用多层感知器分类器对手写数字进行分类

news2024/12/25 1:26:07

使用多层感知器分类器对手写数字进行分类

图 1：多层感知器网络

1.简介

1.1 什么是多层感知器（MLP）？

MLP 是一种监督机器学习 (ML) 算法，属于前馈人工神经网络 [1] 类。该算法本质上是在数据上进行训练以学习函数。给定一组特征和一个目标变量（例如标签），它会学习一个用于分类或回归的非线性函数。在本文中，我们将只关注分类案例。

1.2 MLP和逻辑回归有什么相似之处吗？

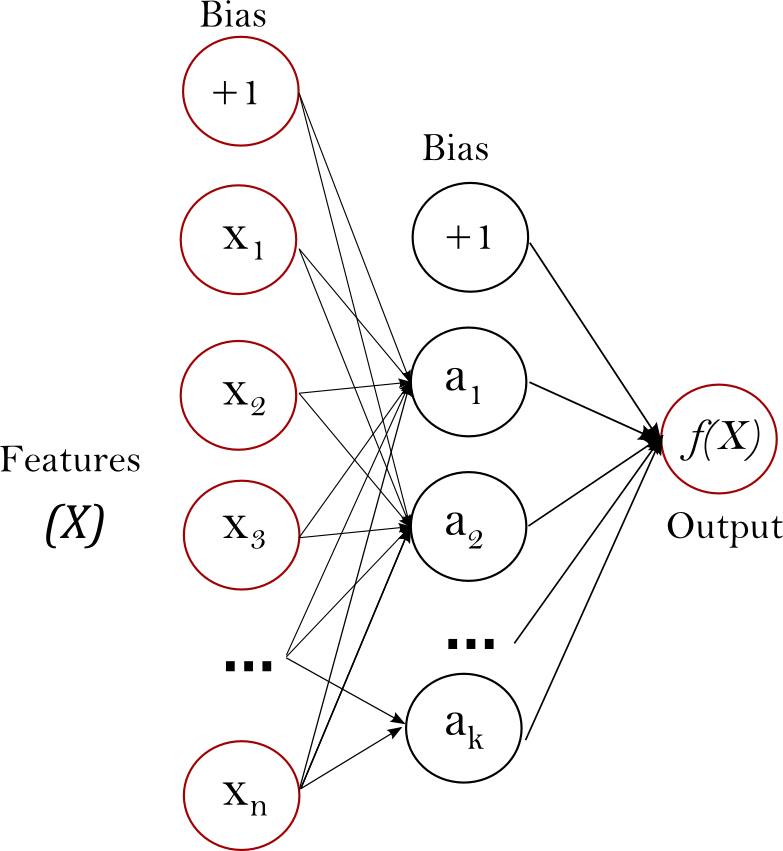
有！逻辑回归只有两层，即输入和输出，但是，在 MLP 模型的情况下，唯一的区别是我们可以有额外的中间非线性层。这些被称为隐藏层。除了输入节点（属于输入层的节点）之外，每个节点都是一个使用非线性激活函数的神经元[1]。由于这种非线性性质，MLP 可以学习复杂的非线性函数，从而区分不可线性分离的数据！请参见下面的图 2，了解具有一个隐藏层的 MLP 分类器的可视化表示。

1.3 MLP 是如何训练的？

MLP 使用反向传播进行训练。

1.4 MLP的主要优缺点.

优点：

可以学习非线性函数，从而分离不可线性分离的数据。
缺点：
隐藏层的损失函数导致非凸优化问题，因此存在局部最小值。
不同的权重初始化可能会导致不同的输出/权重/结果。
MLP 有一些超参数，例如隐藏神经元的数量，需要调整的层数（时间和功耗）。
MLP 可能对特征缩放敏感。

2.使用scikit-learn的Python动手实例

2.1 数据集

对于这个实践示例，我们将使用 MNIST 数据集。 MNIST 数据库是一个著名的手写数字数据库，用于训练多个 ML 模型。有 10 个不同数字的手写图像，因此类别数为 10 （参见图 3）。

注意：由于我们处理图像，因此这些由二维数组表示，并且数据的初始维度是每个图像的 28 by 28 ( 28x28 pixels )。然后二维图像被展平，因此在最后由矢量表示。每个 2D 图像都被转换为维度为 [1, 28x28] = [1, 784] 的 1D 向量。最后，我们的数据集有 784 个特征/变量/列。

图 3：数据集中的一些样本

2.2 数据导入与准备

import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.neural_network import MLPClassifier
# Load data
X, y = fetch_openml("mnist_784", version=1, return_X_y=True)
# Normalize intensity of images to make it in the range [0,1] since 255 is the max (white).
X = X / 255.0

请记住，每个 2D 图像现在都转换为维度为 [1, 28x28] = [1, 784] 的 1D 矢量。我们现在来验证一下。

print(X.shape)

这将返回： (70000, 784) 。我们有 70k 个扁平图像（样本），每个图像包含 784 个像素（28*28=784）（变量/特征）。
因此，输入层权重矩阵的形状为

784 x #neurons_in_1st_hidden_layer.

输出层权重矩阵的形状为

#neurons_in_3rd_hidden_layer x #number_of_classes

2.3 模型训练

现在让我们构建模型、训练它并执行分类。我们将分别使用 3 个隐藏层和 50,20 and 10 个神经元。此外，我们将设置最大迭代次数 100 ，并将学习率设置为 0.1 。这些是我在简介中提到的超参数。我们不会在这里微调它们。

# Split the data into train/test sets
X_train, X_test = X[:60000], X[60000:]
y_train, y_test = y[:60000], y[60000:]
classifier = MLPClassifier(
    hidden_layer_sizes=(50,20,10),
    max_iter=100,
    alpha=1e-4,
    solver="sgd",
    verbose=10,
    random_state=1,
    learning_rate_init=0.1,
)
# fit the model on the training data
classifier.fit(X_train, y_train)

2.4 模型评估

现在，让我们评估模型。我们将估计训练和测试数据和标签的平均准确度。

print("Training set score: %f" % classifier.score(X_train, y_train))
print("Test set score: %f" % classifier.score(X_test, y_test))

训练集分数：

0.998633

测试集分数：

0.970300

2.5 成本函数演变的可视化

训练期间损失减少的速度有多快？让我们制作一个漂亮的图表看一看！

fig, axes = plt.subplots(1, 1)
axes.plot(classifier.loss_curve_, 'o-')
axes.set_xlabel("number of iteration")
axes.set_ylabel("loss")
plt.show()

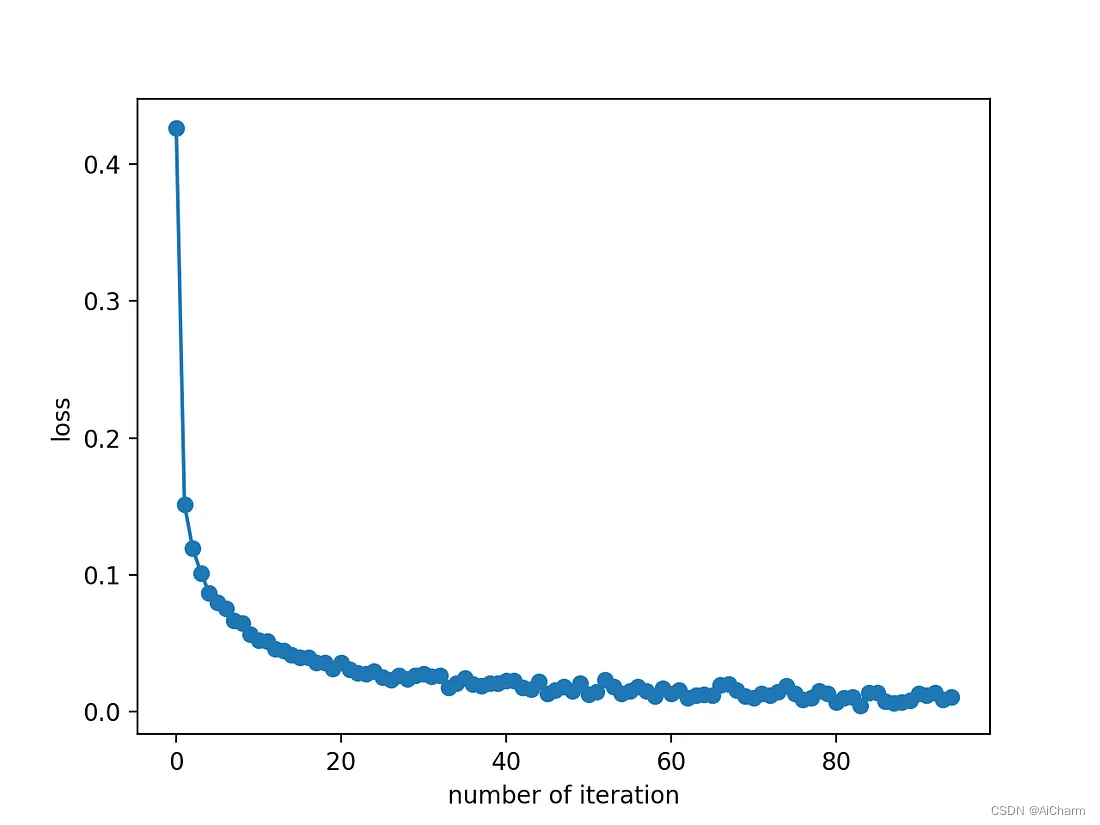
图 4：训练迭代中损失的演变
在这里，我们看到损失在训练期间下降得非常快，并且在 40th 迭代后饱和（请记住，我们将最大 100 次迭代定义为超参数）。

2.6 可视化学习到的权重

这里我们首先需要了解权重（每一层的学习模型参数）是如何存储的。

根据文档，属性 classifier.coefs_ 是形状为 (n_layers-1, ) 的权重数组的列表，其中索引 i 处的权重矩阵表示层 i 和层 i+1 之间的权重。在这个例子中，我们定义了 3 个隐藏层，我们还有输入层和输出层。因此，我们希望层间权重有 4 个权重数组（图 5 中的 in-L1, L1-L2, L2-L3 和 L2-out ）。

类似地， classifier.intercepts_ 是偏置向量列表，其中索引 i 处的向量表示添加到层 i+1 的偏置值。

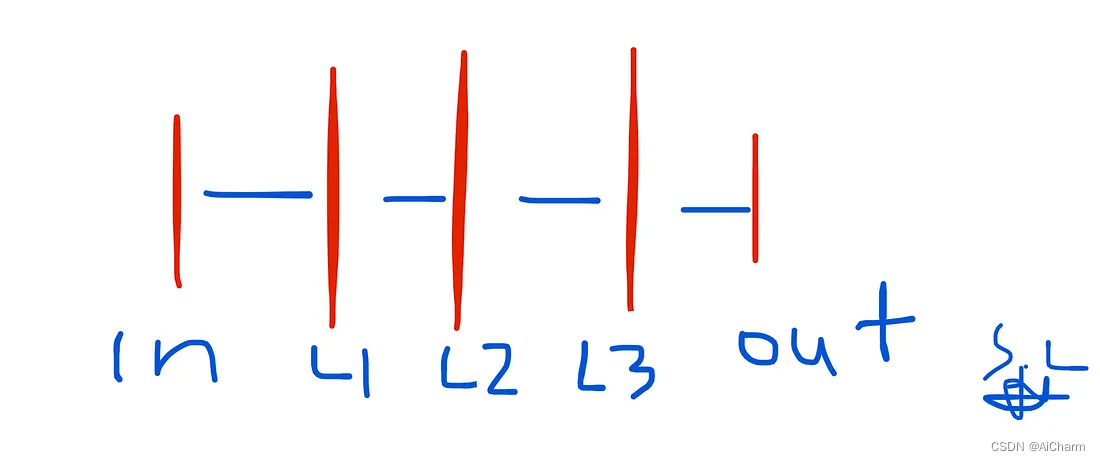
在这里插入图片描述

让我们验证一下：

len(classifier.intercepts_) == len(classifier.coefs_) == 4

正确返回 True 。

输入层权重矩阵的形状为

784 x #neurons_in_1st_hidden_layer.

输出层权重矩阵的形状为

#neurons_in_3rd_hidden_layer x #number_of_classes.

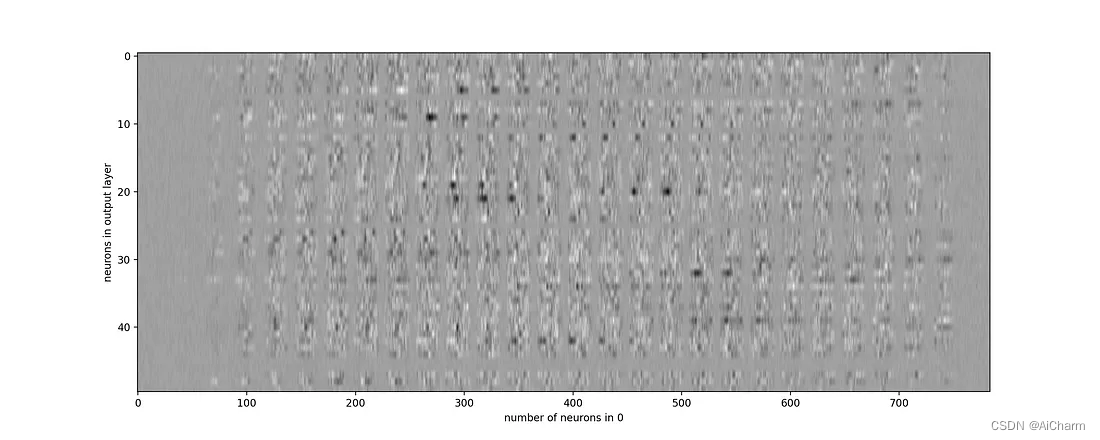
2.7 可视化输入层的学习权重

target_layer = 0 #0 is input, 1 is 1st hidden etc
fig, axes = plt.subplots(1, 1, figsize=(15,6))
axes.imshow(np.transpose(classifier.coefs_[target_layer]), cmap=plt.get_cmap("gray"), aspect="auto")
axes.set_xlabel(f"number of neurons in {target_layer}")
axes.set_ylabel("neurons in output layer")
plt.show()

图 6：输入层和第一个隐藏层之间的神经元学习权重的可视化
将它们重新整形并绘制为 2D 图像。

# choose layer to plot
target_layer = 0 #0 is input, 1 is 1st hidden etc
fig, axes = plt.subplots(4, 4)
vmin, vmax = classifier.coefs_[0].min(), classifier.coefs_[target_layer].max()
for coef, ax in zip(classifier.coefs_[0].T, axes.ravel()):
    ax.matshow(coef.reshape(28, 28), cmap=plt.cm.gray, vmin=0.5 * vmin, vmax=0.5 * vmax)
    ax.set_xticks(())
    ax.set_yticks(())
plt.show()

3.总结

MLP 分类器是一种非常强大的神经网络模型，可以学习复杂数据的非线性函数。该方法使用前向传播来构建权重，然后计算损失。接下来，反向传播用于更新权重，从而减少损失。这是以迭代方式完成的，迭代次数是一个输入超参数，正如我在简介中所解释的那样。其他重要的超参数是每个隐藏层中的神经元数量和隐藏层总数。这些都需要微调。
更多Ai资讯：公主号AiCharm
在这里插入图片描述