一维数组前缀和的概念

前缀和的概念很简单，我们用一维数组的前缀和来举例，有如下一维数组：

arr = [1, 2, 3, 4, 5]

该数组的前缀和数组如下

preSum = [1, 3, 6, 10, 15]

关系如下：

• preSum[0] = arr[0]
• preSum[1] = arr[0] + arr[1]
• preSum[2] = arr[0] + arr[1] + arr[2]
• preSum[3] = arr[0] + arr[1] + arr[2] + arr[3]
• preSum[4] = arr[0] + arr[1] + arr[2] + arr[3] + arr[4]

可以发现前缀和数组元素 preSum[i]的值 其实就是 arr数组 0~i 前缀子数组的和。

而计算得到前缀和数组，可以利用动态规划，其状态转移方程如下：

• preSum[0] = arr[0]
• preSum[i] = preSum[i-1] + arr[i] ； （i  >= 1）

一维数组前缀和的应用

一维前缀和可以用于求解数组任意区间的和。

比如有数组 arr = [1,2,3,4,5]，我们通过动态规划得到其前缀和数组：preSum = [1,3,6,10,15]，现在要求arr给定[l,r]区间范围内元素的和。

一般策略是，for循环遍历arr的l~r索引的元素累加。但是如果给定的区间特别多呢？那就意味着要多次for循环遍历对应区间元素进行累加。这必然产生一个问题：重复计算。

即每次求解给定区间元素和的时间复杂度都是O(n)。

但是利用前缀和，我们就可以在O(1)时间内得出给定区间的元素和。

比如，现在要求arr数组的[l,r]区间的元素和，利用前缀和求解公式如下：

subSum = preSum[r] - preSum[l-1]

比如，arr数组[1,3]区间的和 = preSum[3] - preSum[0] = 10 - 1 = 9

二维矩阵前缀和的概念

二维前缀和即二维矩阵的前缀和，比如现在有如下二维矩阵matrix

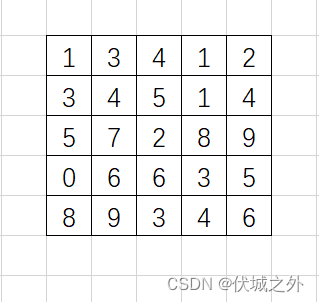
preSum[i][j] 表示 左上角(0,0)坐标到右下角(i, j)坐标范围内元素的和，比如：

preSum[2][3]表示的前缀和求解范围如下

那么我们该如何计算preSum[i][j]呢？

此时同样需要利用动态规划，即利用关联状态之间的转移：

preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + matrix[i][j]

是不是感觉贼复杂的状态转移公式？

下面我们通过画图，来帮助你理解这个公式：

preSum[i][j]其实就是上图黄色区域

preSum[i-1][j] 如下图区域

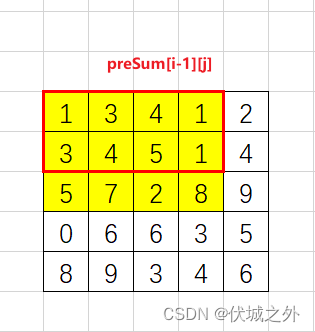
preSum[i][j-1]如下图区域 

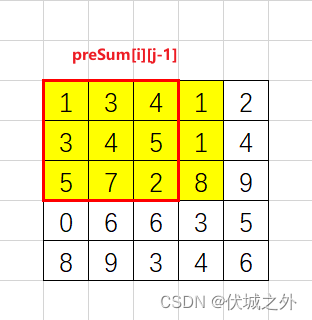
那么preSum[i-1][j] + preSum[i][j-1]是什么样子呢？其实就是如下区域，并且有重叠部分，就是下图颜色比较重的红色区域：

 

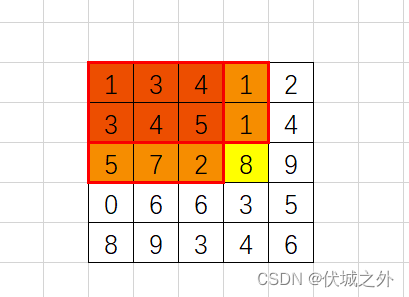
 而这个重叠区域其实就是 preSum[i-1][j-1]。

因此 preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1]其实是如下区域的元素和

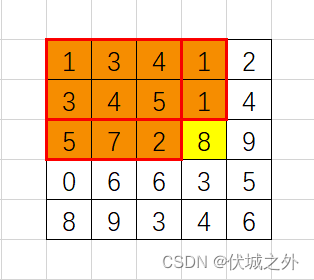
 此时，我们发现该区域和preSum[i][j]区域仅仅只相差了一个matrix[i][j]元素（即上图仅剩的黄色元素）。

因此，得到状态转移方程如下：

preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + matrix[i][j]

而完整的状态状态方程如下：

• preSum[0][0] = matrix[0][0]
• preSum[0][1] = preSum[0][0] + matrix[0][1]
• preSum[1][0] = preSum[0][0] + matrix[1][0]
• preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + matrix[i][j]；（i >=1 && j >=1）

补充的三个红色转移公式，是为了避免第四个公式产生数组越界异常。

二维矩阵前缀和的应用

同一维数组前缀和相同，二维矩阵前缀和也用于在O(1)时间内，求解出二维矩阵中任意矩形范围内元素之和。

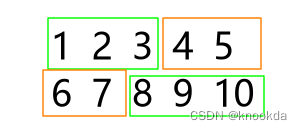
比如求解matrix矩阵中，左上角[i1,j1]到右下角[i2,j2]矩形范围的元素之和，如下图

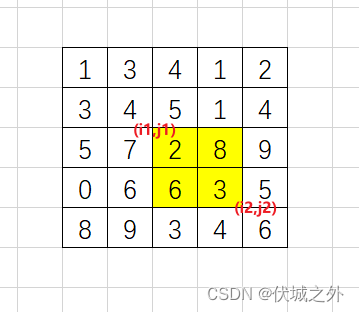
其实这个矩形范围，可以看成是：

(0,0) ~ (i2,j2)  区域  减去 (0,0)~(i2, j1) + (0,0)~(i1, j2) 再加上 (0,0)~(i1,j1)

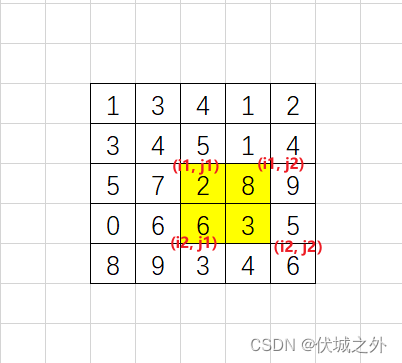
即计算公式如下：

preSum[i2][j2] - (preSum[i2][j1] + preSum[i1][j2]) + preSum[i1][j1]

这样我们基于二维矩阵前缀和，就能用O(1)的时间计算出任意给定矩形范围内元素之和。

一维数组的差分数列

一维数组的差分数组概念也很简单，比如有一维数组arr = [1, 2, 3, 4, 5]，那么arr对应的差分数列即为 diff = [1, 1, 1, 1, 1]

原理是：

• diff[0] = arr[0]
• diff[1] = arr[1] - arr[0]
• diff[2] = arr[2] - arr[1]
• diff[3] = arr[3] - arr[2]
• diff[4] = arr[4] - arr[3]

差分数列的求解很简单，即:

• diff[0] = arr[0]
• diff[i] = arr[i] - arr[i-1]

那么差分数列有什么用呢？

在介绍差分数列的应用之前，我们需要先了解差分数列的一个特性，那就是差分数列，也可以看出一个数组，那么这个数组的前缀和数组是什么呢？

我们来计算一下：

• diffPreSum[0] = diff[0]
• diffPreSum[1] = diff[0] + diff[1]
• diffPreSum[2] = diff[0] + diff[1] + diff[2]
• diffPreSum[3] = diff[0] + diff[1] + diff[2] + diff[3]
• diffPreSum[4] = diff[0] + diff[1] + diff[2] + diff[3] + diff[4]

那么差分数列diff = [1, 1, 1, 1, 1] 对应的前缀和数组diffPreSum = [1, 2, 3, 4, 5]

是不是似曾相识？arr = [1, 2, 3, 4, 5]

没错，arr数组的差分数列是diff，diff的前缀和数组又变回了arr。

即：一个数组arr的差分数列的前缀和数组就是arr

那么为什么diff[4] = 1，diffPreSum[4]就变为了5呢？过程如下：

• diff[4] = arr[4] - arr[3]
• diffPreSum[4] = diff[0] + diff[1] + diff[2] + diff[3] + diff[4]
•                        = arr[0] + (arr[1] - arr[0]) + (arr[2] - arr[1]) + (arr[3] - arr[2] ) + (arr[4] - arr[3])
•                        = arr[4]

扩展：一个数组arr的前缀和数组的差分数列就是arr

即，差分和前缀和可以看成互逆运算。

那么了解了差分数列这个特性有什么用呢？

差分数列通常用于 给一个区间所有元素 统统加上 一个增量。

比如，现在有数组list，现在要给它区间 [l, r] 范围内所有元素加上d。

按照以往思路，我们通常是for循环遍历list数组的 [l, r] 区间每个元素，并给遍历元素+d，这个操作的时间复杂度是O(n)。如果要对多个区间进行+d，那么就需要进行多次for。

但是，我们可以定义一个差分数列 diff，长度和list相同，且数组元素全部初始化为0。

如果要给list数组的 [l, r] 区间每个元素+d，则只需要花费O(1)将:

• diff[l] += d
• diff[r+1] -= d

然后求解diff的前缀和数组即可。

比如：list 长度为5，则初始化差分数列 diff = [0, 0, 0, 0, 0]

现在要给list的[1,3]区间每个元素 + 2，则：

• diff[1] += 2
• diff[4] -= 2

即 diff 差分数列变为 [0, 2, 0, 0, -2]

然后求解diff差分数列的前缀和diffPreSum为：[0, 2, 2, 2, 0]

最后 遍历list，将list[i] += diffPreSum[i] 即可。