01背包除了可以用形象的二维动态数组表示外,还可以使用空间复杂度更低的一维滚动数组。
目录
文章目录
前言
一、滚动数组的基本理解
二、确定dp及其下标含义
三、确定递推公式
四、确定初始化
五、确定遍历顺序
1.用物品(正序)遍历背包(正序)
实现代码:
手写图解:
2.用背包(正序)遍历物品(正序)
实现代码:
手写图解:
3.用物品(正序)遍历背包(逆序)
实现代码:
手写图解: 编辑
总结
前言
晦涩难懂的滚动数组,有两个非常重要的点:①倒序②物品嵌套背包遍历
一、滚动数组的基本理解
我对于滚动数组的理解是:
滚动数组是基于二维数组之上产生的,之所以滚动数组能够用一维的方式去完成和二维同样的工作,原因就是在于这个滚动数组能够重复产生数据,进而有“滚动”的效果。
滚动数组的本质还是二维数组,只是数据不再产生新的行,只在一行上一直进行数据的覆盖更新,因此要特别注意数据污染的情况。
二、确定dp及其下标含义
三、确定递推公式
与二维dp数组相同,dp[j]的状态可以由两种状态得来:
①拿第i件物品(拿了以后,背包容量会减,价值会增加);
②不拿第i件物品;
所以可得:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
四、确定初始化
由递推公式可得:dp[j]是由它之前的数据得来的,也即想要知道dp[j]的数值,就需要知道dp[j-x]的数据。(x是往前推的、未定的下标)
所以初始化只需要初始化dp[0]为0即可。(目前分析来说)
五、确定遍历顺序
与二维数组相同的是,一维dp数组仍然需要遍历物品和背包容量两种变量,只有这样才能模拟出将物品放入背包的过程。
1.用物品(正序)遍历背包(正序)
实现代码:
for (int j = 0; j < bagCapacity; j++)
{
for (int i = 0; i < weight.size(); i++)
{
// 背包容量够放
if (j >= weight[i])
{
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
// 不够放
else
{
dp[j] = dp[j];
}
}
}手写图解:

由此我们可以很明显地看出在一维dp数组的情况下,数据覆盖的时候会发生污染,发现了物品0被放进dp[2]两次。
难道是遍历前后顺序不对?
2.用背包(正序)遍历物品(正序)
实现代码:
for (int i = 0; i < weight.size(); i++)
{
for (int j = 0; j < bagCapacity; j++)
{
// 背包容量够放
if (j >= weight[i])
{
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
// 不够放
else
{
dp[j] = dp[j];
}
}手写图解:

交换后,还是不可避免地发生了数据污染。
由此我们可以知道:
正序遍历的时候会将上一个物品装进背包两回,导致错误,而逆序就可保证dp[j]不受前面数据的影响(这时前面的数据仍然都是0),也就保证了每件物品只被放进去一次。
分析到这,我们也可以知道:初始化必须让整个dp数组的值都初始化为0(后面的dp[j]不能受前面数据的影响)。
3.用物品(正序)遍历背包(逆序)
实现代码:
for (int i = 0; i < weight.size(); i++)
{
for (int j = bagCapacity; j >= 0; j--)
{
// 背包容量够放
if (j >= weight[i])
{
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
// 不够放
else
{
dp[j] = dp[j];
}
}
}手写图解:
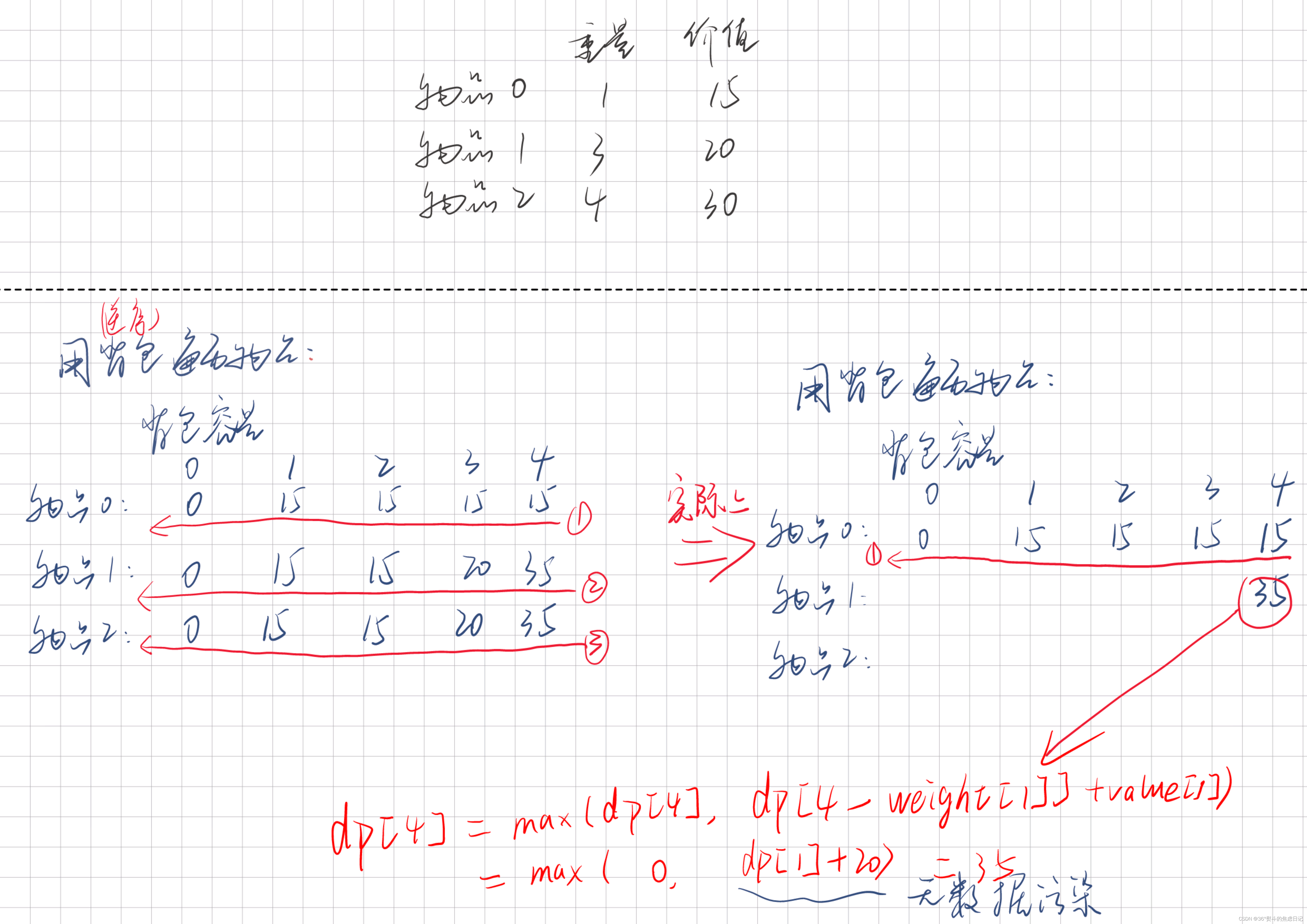
总结
最后我也验证了,既然遍历背包容量的时候需要倒序,那么可不可以再将倒序的背包和正序的物品颠倒位置?
运行结果:
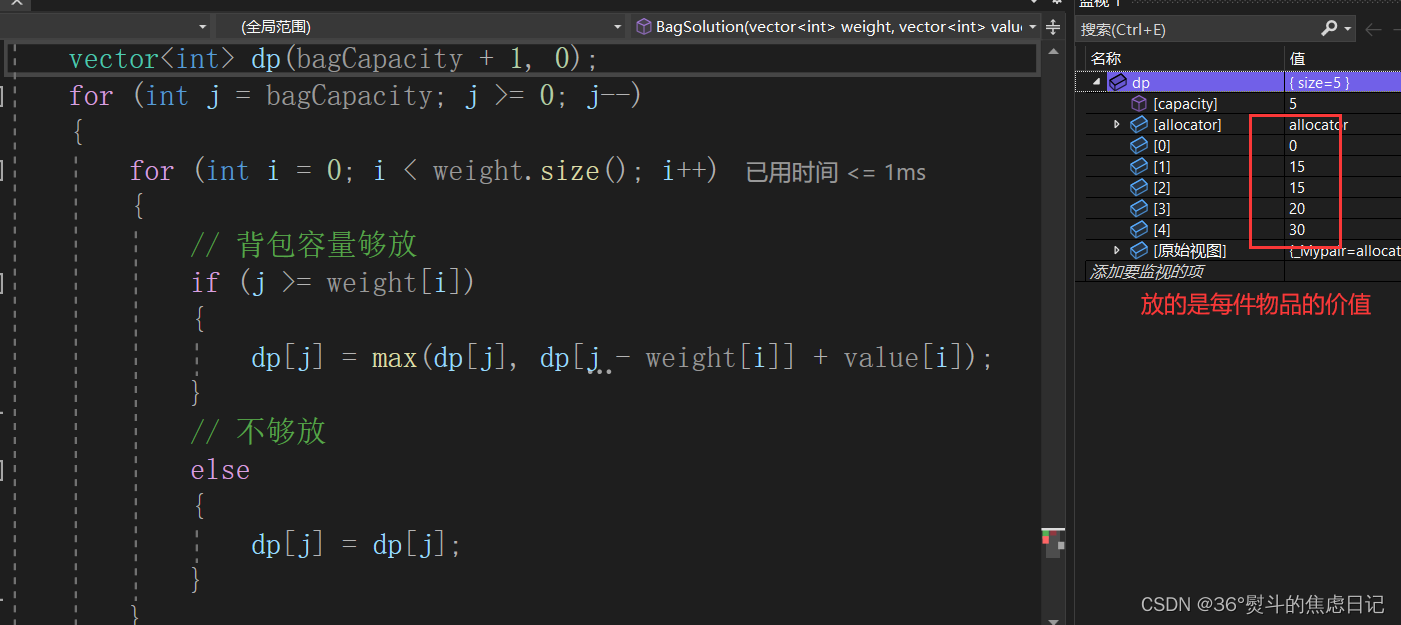
原因是:从后向前遍历背包容量,见到能放进去的物品就跟已经已经在背包里的价值相比较,选择大的,但是这样一来不会发生价值的相加,只是看哪个物品价值高,并且在背包容量范围内,那就放进背包成为dp[j]。
遍历顺序在较复杂的dp题中是非常重要的一环。



![[SSD固态硬盘技术 9] FTL详解](https://img-blog.csdnimg.cn/img_convert/9216fea96be3478986df13d923878edd.png)