最小二乘拟合问题 求解超定方程
首先写这篇博客之前说一个背景,这个最小二乘拟合问题是我在去年面试实习的时候被问到的,然后当时是非常的尴尬,没有回答上来里面的问题。Hhh 所以这篇博客来进行一个补充学习一下下。感觉这个最小二乘问题还是比较重要的,废话不多说,开始讲解!
编辑切换为居中
添加图片注释,不超过 140 字(可选)
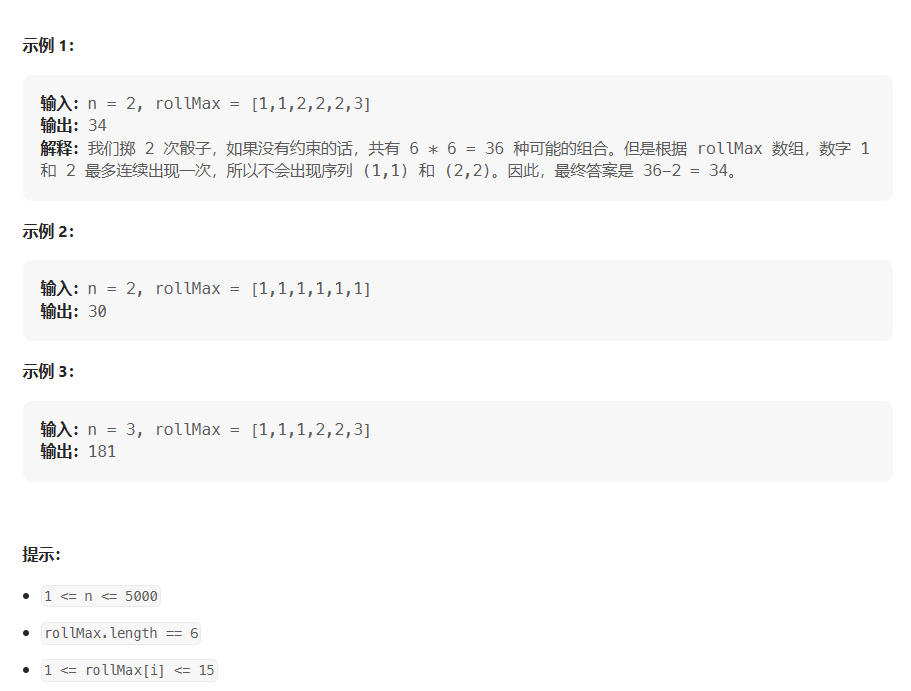
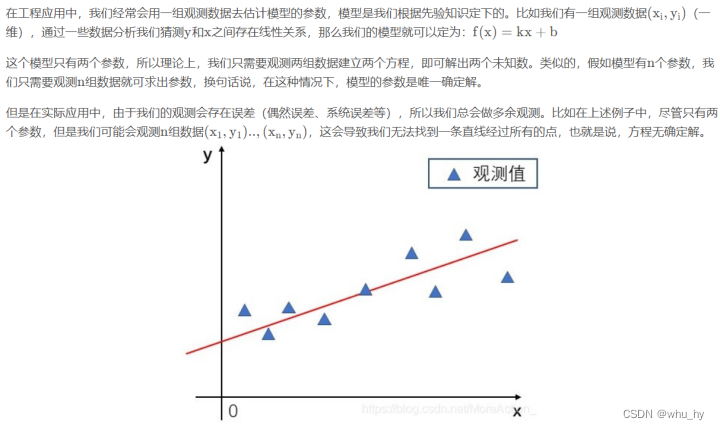
就是说这个背景,有多组观测值的时候如何拟合一条直线让他们的目标函数最小。这也即是求解一个超定方程的问题,因为你观测到了多组数据,而一条直线只有两个参数,那么这多出来的数据必然造成了方程的超定现象。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
画考点! 这里为什么要用二范数作为目标函数,其他范数可不可以呢。这是面试官问我的,当时我可能被问懵了 。。。 然后说了不知道。然后这个问题我之前搜了一下好像是实数域上的范数是等价的,那么二范数可以等价为一范数或者其他。那么这时候就可以说其他范数也可以。但是这里的话,说二范数最接近真实情形的,那么这作为数学和实际生活中的又一个分歧。这里到底为什么能用二范数的话,到下面再写。这里先把背景介绍完再说哈。
高斯证明的误差的平方和最小最能反应实际情况,高斯无敌!

编辑切换为居中
添加图片注释,不超过 140 字(可选)
然后这里的话就是最小二乘求解参数的公式啦!只要你按照这个公式,往里面一代入,那么求解出来的向量就是你所需要求解的参数啦!这个公式的推导也是非常的简单,就是考虑极值点导数为0的情况,然后求导数为0,那么最后一套流程下来以后,得到的解便是所要求解的参数啦!

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这里的话就是最小二乘的几何含义,x是对A矩阵的列向量的线性组合,那么b不在这个组合中。我们就要想办法找一个p向量让他非常接近b向量,那么求出来的ax=p即是原方程的最小二乘解。总的来说,即我们找不到ax=b的解,那么我们找一个p,让它非常接近b,这样求出来的ax=p的解即是最小二乘解,也就是我们所要求解的那个解。
误差平方和相关:
这一部分主要讲解为什么目标函数使用二范数,而不是其他范数。这个地方是偏向于实际生活的,如果按照纯数学的角度来说,实数域上的一切范数都是等价的,那么用啥范数都是无所谓的。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这里使用误差平方法是在各方程的误差之间建立了一种平衡,从而防止某一极端误差取得支配地位,而这有助于揭示系统的更接近真实的状态。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这里的话进行一个快速的介绍。就是说撇开最小二乘不提的话,在求解观测参数的时候我们常用的方法就是最大似然,也即概率相乘,然后取log,然后求导,最后令导数为0,求解出来的那个参数就是最大似然估计出来的参数。然后这里又说了最大似然估计得到的其实就是最小二乘得到的东西,那么这里用最小二乘法其实就是误差满足正态分布的极大似然估计。那么就合情合理地解释了为什么使用误差平方和作为目标函数了。因为它符合误差数据的分布,这样能够更好地拟合模型。
https://blog.csdn.net/MoreAction_/article/details/121591653
上面是链接。
矩阵的正定问题:

编辑切换为居中
添加图片注释,不超过 140 字(可选)
背景介绍,这里求解参数sita的时候,因为有一个求逆的操作,但是里面的矩阵不一定可逆,那么该如何解决呢,本小节讨论这个问题。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
最小二乘法里面如果遇到了不可逆和病态的问题,那么这种情况下就要引入岭回归。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
这里的话在括号里面加了莱姆大乘单位矩阵来保证了求逆运算的可行性。这个是不是非常眼熟!啊 对 就是LM方法,就是视觉slam14讲中介绍完高斯牛顿法以后紧接着介绍了LM方法就是在不可求逆的情况下该怎么让其变成能够求逆的方法。
https://blog.csdn.net/MoreAction_/article/details/125004112
附一个链接。