文章目录
- 互不侵犯
- 矩阵计数
互不侵犯
题目传送门
在N×N的棋盘里面放K个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共8个格子。
升级版的八皇后问题,但是绝不是深搜dfs可以解决的,这是个指数型复杂度的问题,我们只能使用状态压缩DP
我们可以把每一行看作一个二进制数,则我们就可以使用01规定此格子有无国王。
例如每一行为: 0101 则四个位置分别表示: 空,有国王,空,有国王
我们不妨对国王所能攻击到达的 八个位置展开讨论,只要别的国王不在这八个位置中,则就是一种方案数。
因此我们首先判断在一行中左右是否存在相邻的1的情况:我们称左右相邻的这种情况为第一性质
- 判断 i 的右边有没有国王,则就是判断 1的右边是不是也为1,则可以把 i 右移一位,与 i 相与,若结果为0则不是相邻的1
- 判断 i 的左边有没有国王,则就是判断 1的左边是不是也为1,则可以把 i 左移一位,与 i 相与,若结果为0则不是相邻的1

第一性质的判断我们可以通过预处理来求出:
- cnt 数组记录每一行国王出现的数量
- zt数组记录如果左右不相邻为1,则记录这个二进制状态是合法的,因为我们通过这种状态来往下求出下面的行。
我们不光要使得 第一性质 即行左右满足不相邻为1,还要使得行的左上右下,左下右上,正上正下都满足不相邻为1,我们称它为第二性质
第二性质如何判断? 注意我们在这时已经转移到了 两行之间的状态,所以说应该是 i 与 i-1 行,
- 正上正下: 只需满足 i & j 等于0 即可满足。
- 左上右下:只需满足 (j<<1)&1 等于0 即可。
- 左下右上: 只需满足 (i<<1)&j 等于0 即可。
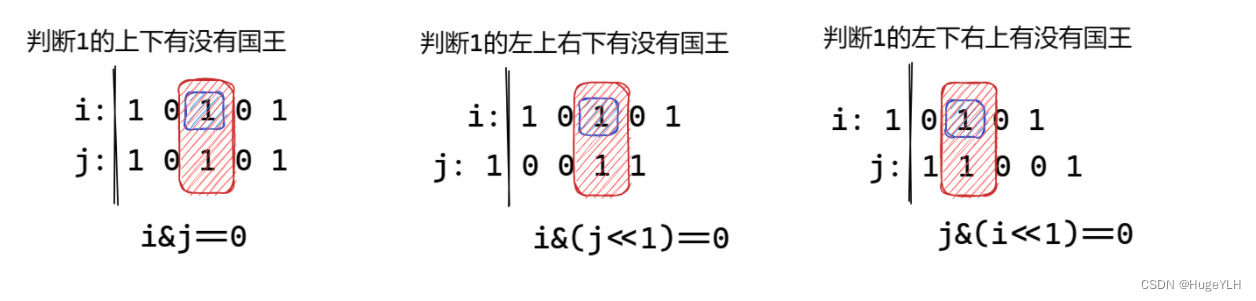
如果它既满足第一性质,也满足第二性质,则我们就可以通过状态转移来转移状态:
定义dp[i] [j] [S] :表示第i行,选择j个国王的状态为S,的时候的方案数
注意:此时的S为 一个二进制数字,表示满足的同一行 第一性质的二进制数字,例如 001,010 ,100,101 都是满足的第一性质的二进制数字,因此只要我们的一行满足了,我们便可以通过枚举每一行加之第二性质的判断来使得整个棋盘都满足第一和第二性质
状态转移方程如下:
d
p
[
i
]
[
j
]
[
s
1
]
+
=
d
p
[
i
−
1
]
[
j
−
c
n
t
[
s
1
]
]
[
s
2
]
dp[i][j][s1] +=dp[i-1][j-cnt[s1]][s2]
dp[i][j][s1]+=dp[i−1][j−cnt[s1]][s2]
解释:第 i 行选 j 个国王的状态 s1 的方案数的 += 第 i-1行,选 j - cnt[ s1 ] 个国王的状态 s2 的方案数
其中 cnt 记录了某一个状态的国王个数(即1的个数),通过 zt 数组的值来获得,zt数组记录状态,cnt[s1]就等于 s1状态的国王的数量
//TODO: Write code here
int n,m;
const int N=1e3+10;
int nums[N],dp[10][100][2000];//i行,j个国王,k个状态
int cnt[N],zt[N];//cnt[i]表示第i行国王的数量,zt[i]表示所有满足条件的左右不相邻的状态
int num;//所有可能的状态总数
void init()
{
/*
预处理行内的相邻的情况: 保证行内,左右的数字不都是1
*/
for (int i=0;i<(1<<n);i++)
{
int temp=0,s=i;
while (s)
{
if (s&1) temp++;//如果最后一位是1
s>>=1;
}
cnt[i]=temp; //第i行数字的二进制的国王数量
if (((i>>1)&i)==0 && ((i<<1)&i)==0) zt[++num]=i;//左右不相邻,这一状态合法
}
}
signed main()
{
cin>>n>>m;
//首先预处理行内的情况
init();
/*
dp[i][j][k]表示第i行有j个国王,状态为k的方案数
*/
//然后处理行之间的情况
dp[0][0][0]=1;
for (int i=1;i<=n;i++)//枚举每一行
{
for (int l=1;l<=num;l++)//枚举第i行的状态
{
int s1=zt[l];//获得第i行的状态,就是一个二进制数字:0代表空,1代表国王
for (int k=1;k<=num;k++)//枚举第i-1行的状态
{
int s2=zt[k];//获得第i-1行的状态,就是一个二进制数字:0代表空,1代表国王
//第i行与第i-1行的上下,左上右下,左下右上都不存在相邻的1
if ((s1&s2)==0 && (s1&(s2>>1))==0 && ((s2<<1)&s1)==0)
{
for (int j=0;j<=m;j++)//枚举国王的个数
{
if (j-cnt[s1]>=0)
{
dp[i][j][s1]+=dp[i-1][j-cnt[s1]][s2];
}
}
}
}
}
}
int ans=0;
for (int i=1;i<=num;i++)//枚举所有的状态
{
ans+=dp[n][m][zt[i]];//累加第n行选择m个国王的数量
}
cout<<ans;
#define one 1
return 0;
}
矩阵计数
矩阵计数 - 蓝桥云课 (lanqiao.cn)
一个 �×�N×M 的方格矩阵,每一个方格中包含一个字符 O 或者字符 X。
要求矩阵中不存在连续一行 3 个 X 或者连续一列 3 个 X。
问这样的矩阵一共有多少种?
这道题目与上面的《互不侵犯》较为相似,上题让我们找到满足国王在它的周围八个方向不能存在别人的总方案数,而这道题目让我们在 一行和一列中不能连续出现 3 个 x
我们像之前一样,首先把 每一行的状态预处理出来,然后我们便可以在通过for循环枚举每一行接着往下求。
进行预处理,我们称之为 第一性质,即首先要满足一行中不能连续出现三个X,我们可以通过以下的代码解决:
- check传入一个参数,通过 对传入的这个参数进行移位操作,如果出现了 计数大于等于3,则代表出现了连续的 XXX,因此我们此时就不能选用这个状态,返回true,返回false才是我们需要的正确结果
- 在init中我们枚举的一行的最大状态为 111,最小为 000,这与 m 列数有关,不要写成 n行数
- 记录满足条件的状态,存储合法状态在 zt 数组中
bool check(int num)
{
int c = 0;
while (num)
{
if ((num & 1)==1) c++;
else c = 0;
if (c >= 3)
{
return true; //出现了三种连续的1
}
num >>= 1;
}
return false;
}
void init()
{
//预处理每行
for (int i = 0; i <(1<<m); i++)//最大111状态 最小000状态
{
if (!check(i))
{
zt[++num] = i; //统计合法的状态个数,并存储
}
}
}
我们设 dp 数组为 dp[i] [j] [k] 表示以第 i 行 具有的 j 状态,第 i-1 行具有的 k 状态所表示的最大的方案数
即,我们的dp数组每次保留两行,因此我们可以通过当前行与前一行的 dp数组 来共同表示一个第三行。
状态转移方程:
d
p
[
i
]
[
z
t
[
j
]
]
[
z
t
[
k
]
]
+
=
d
p
[
i
−
1
]
[
z
t
[
k
]
]
[
z
t
[
p
]
]
dp[i][zt[j]][zt[k]]+=dp[i-1][zt[k]][zt[p]]
dp[i][zt[j]][zt[k]]+=dp[i−1][zt[k]][zt[p]]
我们通过一个四重循环来解决这个问题,首先枚举行数,然后枚举三个状态,只有当 三个状态的与运算为0的时候,则此时满足第二性质,意味着这一列不会有三个连续的 X,此时我们便可以利用这三个状态进行状态转移
- 四重for循环前要做的准备:
- 因为我们的需要枚举连续三行的状态,如果当 i =1的时候,它具有 前一行为0,但是没有前一行的前一行,因此我们需要把 dp[1] [zt[i]] [0] 初始化为0,代表这个状态默认为0方案
- 结果的查找:
- 寻找一个最大值,在最后一行 n中,枚举n的状态与前一行的状态
AC code
#include <bits/stdc++.h>
using namespace std;
#define int long long
//状压DP:矩阵计数
namespace test48
{
int n, m;
const int N = 1005;
int dp[1<<6][1<<6][1<<6];//从i行选择j个X状态为S的方案数
int zt[N],num;//cnt存储每一行的X的数量 zt存储这一个合法的状态
bool check(int num)
{
int c = 0;
while (num)
{
if ((num & 1)==1) c++;
else c = 0;
if (c >= 3)
{
return true; //出现了三种连续的1
}
num >>= 1;
}
return false;
}
void init()
{
//预处理每行
for (int i = 0; i <(1<<m); i++)//最大111状态 最小000状态
{
if (!check(i))
{
zt[++num] = i; //统计合法的状态个数,并存储
}
}
}
void test()
{
cin >> n >> m;
//第一性质:左右不相邻
init();
for (int i = 1; i <= num; i++)
{
dp[1][zt[i]][0] = 1;
}
for (int i = 1; i <= n; i++)
{
for (int p = 1; p <= num; p++)//枚举第i行
{
int s1 = zt[p];
for (int l = 1; l <= num; l++)//枚举第i-1行
{
int s2 = zt[l];
for (int r = 1; r <= num; r++)//枚举第i-2行
{
int s3 = zt[r];
//如果正上与正下不相邻,则满足第二性质
if ((s1 & s2 & s3) == 0)//三行不同时为1则是一个合法状态
{
//第i行的合法状态为s1,前一行的合法状态为s2 -->
//第i-1行的合法状态为s2,第i-2行的合法状态为s3
dp[i][s1][s2] += dp[i - 1][s2][s3];
}
}
}
}
}
int ans = 0;
for (int i = 1; i <= num; i++)
{
for (int j = 1; j <= num; j++)
{
ans += dp[n][zt[i]][zt[j]];
}
}
cout << ans;
}
}
signed main()
{
using namespace test48;
test48::test();
return 0;
}
态为s3
dp[i][s1][s2] += dp[i - 1][s2][s3];
}
}
}
}
}
int ans = 0;
for (int i = 1; i <= num; i++)
{
for (int j = 1; j <= num; j++)
{
ans += dp[n][zt[i]][zt[j]];
}
}
cout << ans;
}
}
signed main()
{
using namespace test48;
test48::test();
return 0;
}







![[Golang实战]如何快速接入chatgpt/openai?[引入go-gpt3][新手开箱可用]](https://img-blog.csdnimg.cn/7cd791742c7c43899aac49236c96e35b.png)