一、树与二叉树

在这里插入图片描述

二、二叉树

1.二叉树：度不超过2的树（度：树的分支），每个节点最多有两个孩子节点，两个孩子节点被区分为左孩子节点和右孩子节点。
2.满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
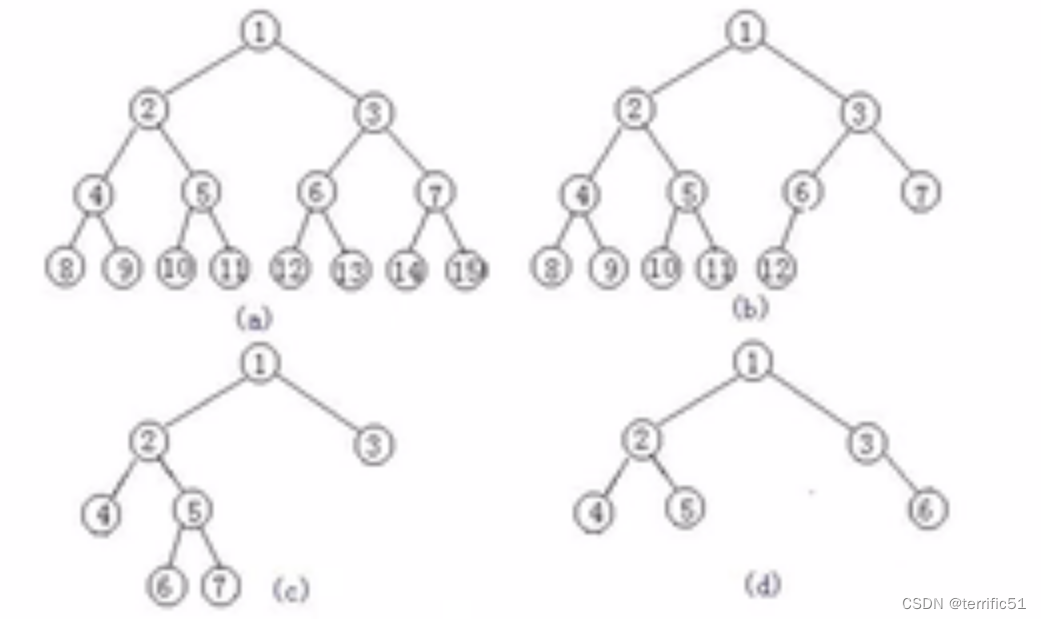
在这里插入图片描述
(a)满二叉树；(b)完全二叉树；©(d)非满二叉树、非完全二叉树
3.二叉树的存储方式——链式存储方式，顺序存储（列表）方式

顺序存储

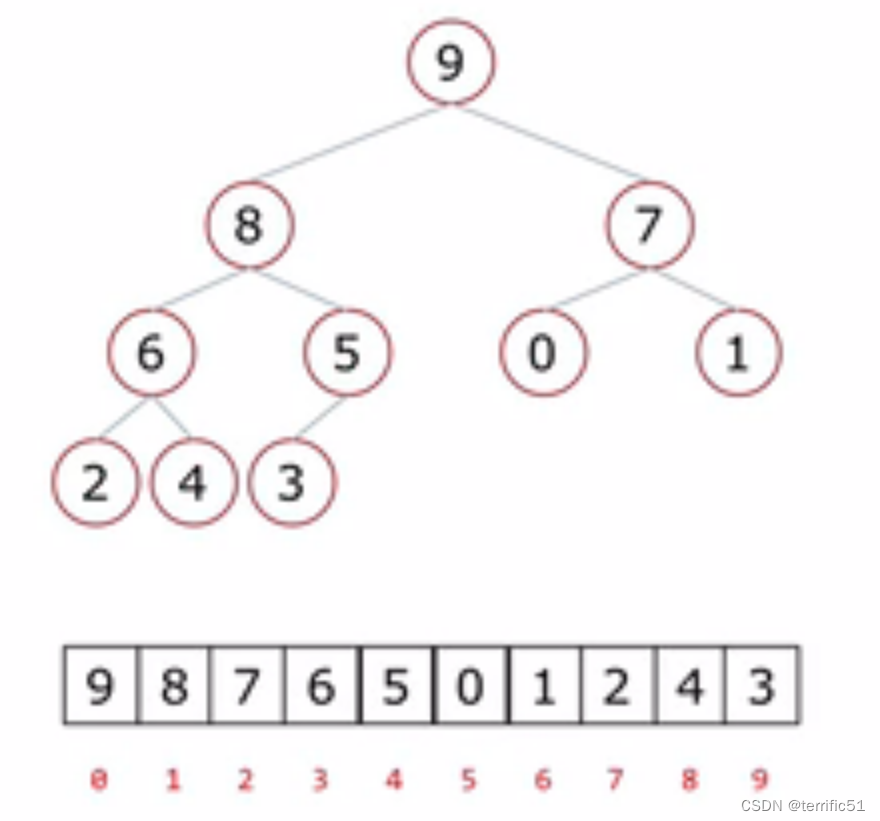
1.父节点和左孩子节点的编号下标有什么关系?
0-1 1-3 2-5 3-7 4-9
i→2i+1
2.父节点和右孩子节点的编号下标有什么关系?
0-2 1-4 2-6 3-8 4-10
i→2i+2

三、堆排序

1.堆:一种特殊的完全二叉树结构
大根堆:一棵完全二叉树，满足任一节点都比其孩子节点大
小根堆:一棵完全二叉树，满足任一节点都比其孩子节点小

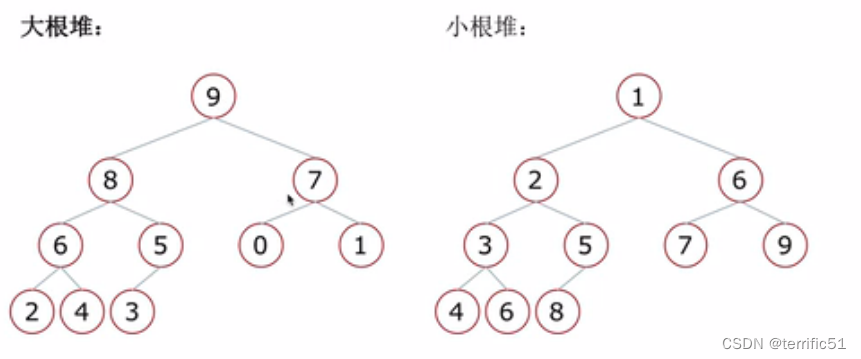
在这里插入图片描述
2.堆的向下调整：当根节点的左右子树都是堆时，可以通过一次向下的调整来将其变换成一个堆。
3.堆排序过程

1.建立堆；
2.得到堆顶元素，为最大元素
3.去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。
4.堆顶元素为第二大元素。
5.重复步骤3，直到堆变空。

def sift(li,low,high):
    """
    :param li:列表
    :param low:堆的根节点位置
    :param high:堆的最后一个元素的位置
    :return:
    """
    i=low #i最开始指向根节点
    j=2*i+1 #j开始是左孩子
    tmp=li[low] #把堆顶存起来
    while j<=high: #只要j位置有数
        if j+1<=high and li[j+1]>li[j]: #如果右孩子有并且比较大
            j=j+1 #j指向右孩子
        if li[j]>tmp: 
            li[i]=li[j]
            i=j      #往下看一层
            j=2*i+1
        else:      #tmp更大，把tmp放到i的位置上
            li[i]=tmp #把tmp放到某一级领导位置上
            break
    else:
        li[i]=tmp #把tmp放到叶子节点上

时间复杂度O（logn）

def heap_sort(li):
    n=len(li)
    for i in range((n-2)//2,-1,-1):#孩子是n-1,孩子的父亲是(n-2)//2,父亲是孩子减一除以2.(n-2)//2向后遍历到0.
        #i表示建堆的时候调整的部分的根的下标
        sift(li,i,n-1)
    #建堆完成
    for i in range(n-1,-1,-1):
        #i指向当前堆的最后一个元素
        li[0],li[i]=li[i],li[0]
        sift(li,0,i-1) #i-1是新的high

时间复杂度O（nlogn）*O（nlogn）

四、内置模块heapq

从小到大的优先队列

import heapq
import random

li=list(range(100))
random.shuffle(li)

print(li)

heapq.heapify(li) #建堆

n=len(li)
for i in range(n):
    print(heapq.heappop(li),end=',')

在这里插入图片描述

五、topk问题

现在有n个数，设计算法得到前k大的数。(k<n)

例如：微博热搜榜
解决思路:
1.排序后切片 O(nlogn)
2.冒泡排序、插入排序、选择排序 O(kn)
3.堆排序 O(nlogk)
1取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数。
2依次向后遍历原列表，对于列表中的元素，如果小于堆顶，则忽略该元素;如果大于堆顶，则将堆顶更换为该元素，并且对堆进行一次调整;
3*遍历列表所有元素后，倒序弹出堆顶。

实现

def sift(li,low,high):
    """
    :param li:列表
    :param low:堆的根节点位置
    :param high:堆的最后一个元素的位置
    :return:
    """
    i=low #i最开始指向根节点
    j=2*i+1 #j开始是左孩子
    tmp=li[low] #把堆顶存起来
    while j<=high: #只要j位置有数
        if j+1<=high and li[j+1]<li[j]: #如果右孩子有并且比较小
            j=j+1 
        if li[j]<tmp: 
            li[i]=li[j]
            i=j      
            j=2*i+1
        else:      
            li[i]=tmp 
            break
    else:
        li[i]=tmp #把tmp放到叶子节点上
    
def topk(li,k):
    heap=li[0:k]
    for i in range((k-2)//2,-1,-1):
        sift(heap,i,k-1)
    #1.建堆
    for i in range(k,len(li)-1):
        if li[i]>heap[0]:
            heap[0]=li[i]
            sift(heap,0,k-1)
    #2.遍历
    for i in range(k-1,-1,-1):
        #i指向当前堆的最后一个元素
        heap[0],heap[i]=heap[i],heap[0]
        sift(heap,0,i-1) #i-1是新的high
    #3.出数
    return heap

import random
li=list(range(1000))
random.shuffle(li)

print(topk(li,10))