1223. 掷骰子模拟

题目描述

有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。

不过我们在使用它时有个约束，就是使得投掷骰子时，连续掷出数字 i 的次数不能超过 rollMax[i]（i 从 1 开始编号）。

现在，给你一个整数数组 rollMax 和一个整数 n，请你来计算掷 n 次骰子可得到的不同点数序列的数量。

假如两个序列中至少存在一个元素不同，就认为这两个序列是不同的。由于答案可能很大，所以请返回模 10^9 + 7 之后的结果。

示例 1

输入：n = 2, rollMax = [1,1,2,2,2,3]
输出：34
解释：我们掷 2 次骰子，如果没有约束的话，共有 6 * 6 = 36 种可能的组合。但是根据 rollMax 数组，数字 1 和 2 最多连续出现一次，所以不会出现序列 (1,1) 和 (2,2)。因此，最终答案是 36-2 = 34。

示例 2

输入：n = 2, rollMax = [1,1,1,1,1,1]
输出：30

示例 3

输入：n = 3, rollMax = [1,1,1,2,2,3]
输出：181

提示

1 <= n <= 5000
rollMax.length == 6
1 <= rollMax[i] <= 15

算法一：动态规划

思路

首先，创建一个二维 dp 数组；
dp[i][j] 表示第 i 次掷骰子时，数字 j 出现的可能的序列总数，也就是说，第 i 次掷出的数字是 j 所有可能的序列数，其中 1 <= i <= n ， 1 <= j <= 6 。
显然， dp[1][1],dp[1][2]… dp[1][6]均为 1 ，所以，最后结果有效序列总数就是 sum (dp[n][1] + dp[n][2] + … + dp[n][6]) ， sum为求和函数。
那么，如何计算第i次骰子掷出时，掷出数字为j的序列总数为多少呢？仔细思考一下dp[i][j]和什么有关?
- 第一: dp[i][j] 和dp[i-1][j]有关，不仅如此，dp[i][j] 和 dp[i-1][1], dp[i-1][2],…dp[i-1][6]都有关；
- 第二: 由于连续数字限制，dp[i][j]还和 dp[i-rollMax[j-1]][1],…,dp[i-rollMax[j-1]][6]均有关；
- 所以，第i次掷出骰子的序列总数只和第i-1次掷出骰子的序列总数，以及第i-rollMax[j-1]次掷出骰子的序列总数有关。
- 详细例子看题解。
- 状态方程为：
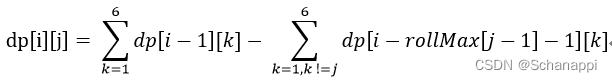
需要主要对大数的处理，使用 int 型很容易越界；
另外，代码中有一个特殊条件的判断，当 idx == 0 时，ans 直接减一；此时，第 1 次 ~ 第 i - 1次掷出的都是 k ，即出现了序列 kkk…kk ，因此不合法的情况只有一种，所以减一。

算法情况

时间复杂度：O（6n），即O（n）；
空间复杂度：O（7（n+1）），即 O（n）。

在这里插入图片描述

代码

class Solution {
public:
    const int MOD = 1e9 + 7;
    typedef long long LL;

    int dieSimulator(int n, vector<int>& rollMax) {
        vector<vector<LL> > dp(n+1, vector<LL>(7));
        // 初始化
        for (int j = 1; j <= 6; j++) {
            dp[1][j] = 1;
        }
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= 6; j++) {
                // 加入第 i-1 次得所有可能序列总数
                LL ans = accumulate(dp[i-1].begin(), dp[i-1].end(), 0LL);
                int idx = i - 1 - rollMax[j-1];
                if (idx >= 1) {
                    // 减去 i - 1 - rollMax[j-1]次掷出除j外其他五个数的所有序列总数
                    ans = accumulate(dp[idx].begin(), dp[idx].end(), ans, [&](LL init, LL e) {
                        return init + MOD - e;
                    });
                    ans += dp[idx][j];
                }else if (idx == 0) {
                    // 特殊情况处理
                    ans -= 1;
                }
                dp[i][j] = ans % MOD;
            }
        }
        return accumulate(dp[n].begin(), dp[n].end(), 0LL) % MOD;
    }
};