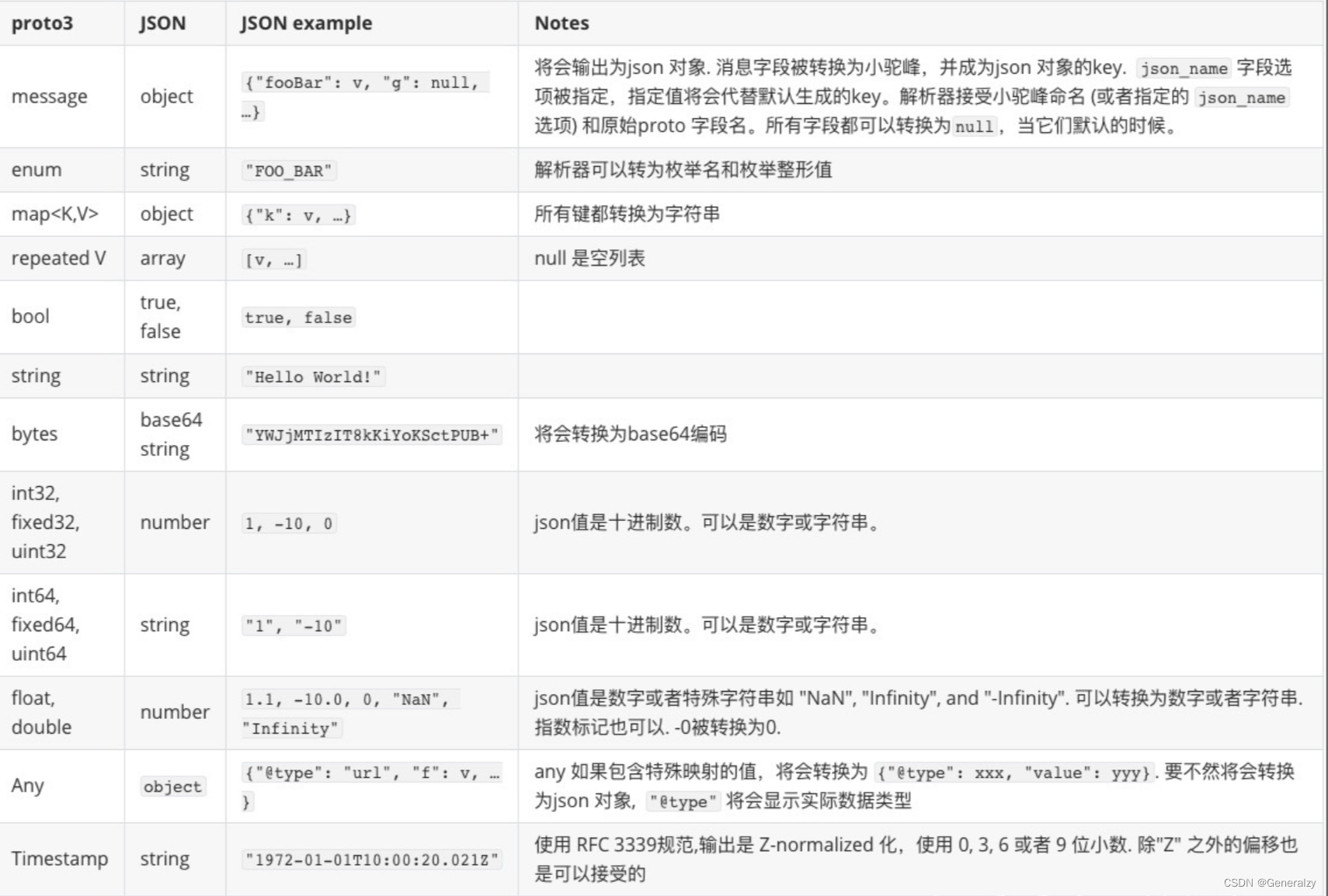
2017-PMLR-Neural Message Passing for Quantum Chemistry

Paper: https://arxiv.org/pdf/1704.01212.pdf
Code: https://github.com/brain-research/mpnn
量子化学的神经信息传递
这篇文献作者主要是总结了先前神经网络模型的共性,提出了一种消息传递神经网络(MPNN)的单一通用框架,并在此框架内探索其他新颖的变化。在重要的分子性质预测基准上使用MPNN展示了最先进的结果。
MPNN框架如下图所示:
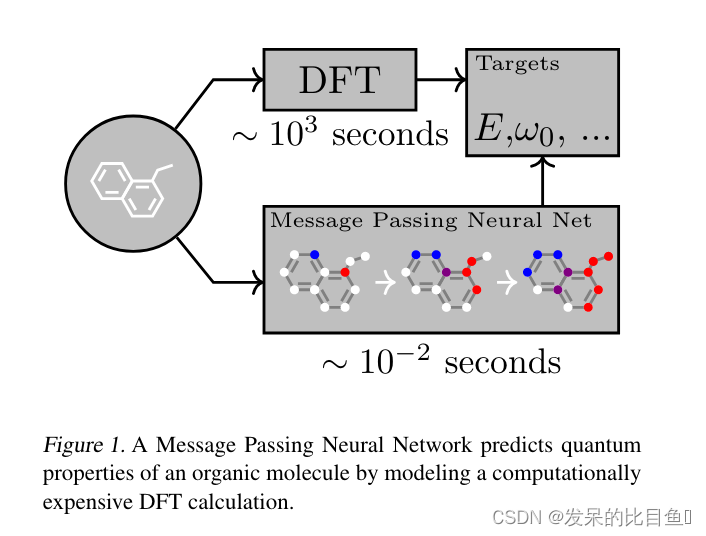
主要贡献:
-
开发了一种MPNN,可在所有13个目标上实现最先进的结果,并预测13个目标中11个目标的DFT在化学精度范围内。
-
开发了几种不同的MPNN,可以预测DFT在13个目标中的5个的化学精度范围内,同时仅对分子的拓扑结构进行操作(没有空间信息作为输入)。
-
开发了一种通用方法,用于训练具有更大节点表示的 MPNN,而不会相应增加计算时间或内存,与以前的高维节点表示的 MPNN 相比,节省了大量成本。
消息传递神经网络
MPNN模型:节点特征
x
v
x_v
xv和边缘特征
e
v
w
e_{vw}
evw 的无向图
G
G
G 。正向传递有两个阶段,消息传递阶段和Readout阶段。消息传递阶段运行T个时间步长,并根据消息函数
M
t
M_t
Mt和顶点更新函数
U
t
U_t
Ut进行定义。在消息传递阶段,图中每个节点的隐藏状态
h
v
t
h^t_v
hvt根据消息
m
v
t
+
1
m^{t+1}_v
mvt+1根据
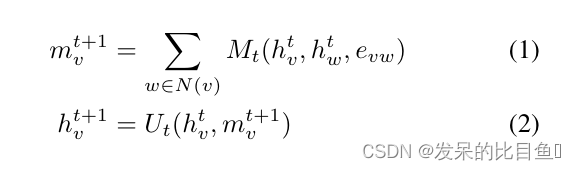
其中,在总和中,
N
(
v
)
N (v)
N(v) 表示图
G
G
G 中
v
v
v 的邻居。readout阶段使用一些Readout函数
R
R
R 根据
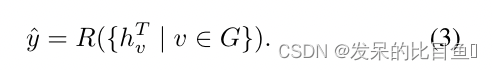
消息函数
M
t
M_t
Mt、顶点更新函数
U
t
U_t
Ut和readout函数
R
R
R 都是学习的可微函数。
R
R
R 在节点状态集上运行,并且必须对节点状态的排列不变,以便 MPNN 对图同构不变。作者通过指定使用的消息函数
M
t
M_t
Mt、顶点更新函数
U
t
U_t
Ut 和readout函数
R
R
R来定义文献中的先前模型。
先前模型
- 用于学习分子指纹的卷积网络
- 门控图神经网络
- 交互网络
- 分子图卷积
- 深度张量神经网络
- 基于拉普拉斯方法
MPNN 变体
作者使用 d d d 来表示图中每个节点的内部隐藏表示的维度,并使用 n n n来表示图中节点的数量。对 MPNN 的实现通常运行在有向图上,具有用于传入和传出边缘的单独消息通道,在这种情况下,传入消息 m v m_v mv是 m v i n m^{in}_v mvin和 m v o u t m^{out}_v mvout的串联。将该图视为有向图,其中每个原始边都成为具有相同标签的传入边和传出边。请注意,边的方向没有什么特别之处,它只与参数绑定有关。将无向图视为有向图意味着消息通道的大小为 2d 而不是 d。
消息函数
矩阵乘法: 从 GG-NN 中使用的消息函数开始,该函数由等式定义
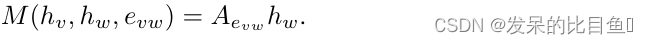
边缘网络: 为了允许向量值边特征,提出了消息函数
M
(
h
v
,
h
w
,
e
v
w
)
=
A
(
e
v
w
)
h
w
M(hv, h_w, e_{vw}) = A(e_{vw})h_w
M(hv,hw,evw)=A(evw)hw,其中
A
(
e
v
w
)
A(e_{vw})
A(evw) 是一个神经网络,它将边向量
e
v
w
e_{vw}
evw 映射到
d
×
d
d × d
d×d 矩阵。
对消息:矩阵乘法规则的一个属性是,从节点 w w w到节点 v v v 的消息只是隐藏状态 h w h_w hw 和边缘 e v w e_{vw} evw 的函数。特别是,它不依赖于隐藏状态 h v t h^t_v hvt。理论上,如果允许节点消息同时依赖于源节点和目标节点,则网络可能能够更有效地使用消息通道。这里,沿边 e e e 从 w w w 到 v v v 的消息是 m w v = f ( h w t , h v t , e v w ) m_{wv} = f(h^t_w, h^t_v, e_{vw}) mwv=f(hwt,hvt,evw),其中 f f f是一个神经网络。将上述消息函数应用于有向图时,使用了两个单独的函数, M i n M_{in} Min和 M o u t M_{out} Mout。哪个函数应用于特定边 e v w e_{vw} evw取决于该边的方向。
虚拟图元素
探索了两种不同的方法来更改消息在整个模型中的传递方式。最简单的修改涉及为未连接的节点对添加单独的“虚拟”边缘类型。这可以作为数据预处理步骤实现,并允许信息在传播阶段长距离传播。
Readout功能
尝试了两个Readout功能。首先是GG-NN中使用的Readout函数,由公式4定义。该模型首先将线性投影应用于每个元组 ( h v T , x v ) (h_v^T,x_v) (hvT,xv),然后将投影元组的集合 T = { ( h v T , x v ) } T = \{(h_v^T,x_v)\} T={(hvT,xv)}作为输入。然后,经过 M 个计算步骤后,set2set 模型生成一个图级嵌入 q ∗ q^∗ q∗,该嵌入与元组 T 的顺序不变。
Multiple Towers
为了解决
O
(
n
2
d
2
)
O(n^2d^2)
O(n2d2)时间复杂度,我们将
d
d
d 维节点嵌入
h
v
t
h^t_v
hvt 分解为
k
k
k 个不同的
d
/
k
d/k
d/k 维嵌入
h
v
t
,
k
h^{t,k}_v
hvt,k,并分别对
k
k
k 个副本中的每个副本运行传播步骤,以获得临时嵌入
h
~
v
t
+
1
,
k
,
v
∈
G
{ \tilde{h}^{t+1,k}_v , v \in G}
h~vt+1,k,v∈G,为每个副本使用单独的消息和更新函数。根据方程将每个节点的
k
k
k 个临时嵌入混合在一起
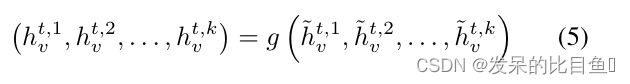
输入表征
有关所有特征列表,请参见表 1。

其中:
**化学图:**在没有距离信息的情况下,邻接矩阵条目是离散键类型:单键、双键、三键或芳烃键类型。
距离箱:矩阵乘法消息函数假定离散的边类型,因此为了包含距离信息,将绑定距离分成 10 个箱。
原始距离特征: 当使用在向量值边上操作的消息函数时,邻接矩阵的条目是5维的,其中第一维表示原子对之间的欧氏距离,其余四个是键类型的一个热编码。
QM9 Dataset
数据集中的分子由氢 (H)、碳( C)、氧(O)、氮(N)和氟(F)原子组成,最多包含 9 个重(非氢)原子。大约134k个药物样的有机分子,它们跨越了广泛的化学领域。
结果

在表2中,MPNN 在 13 目标中的 11 个目标上实现了化学精度,在所有 13 个目标上都达到了最先进的水平。
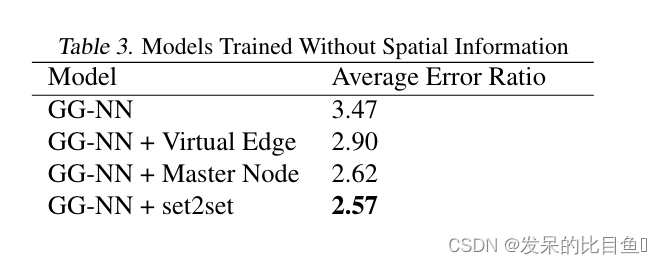
表 3 中,这三种GG-NN模型修改有助于所有 13 个目标,并且 Set2Set 输出在 13 个目标中的 5 个目标上实现了化学精度。