目录
前言
监督学习 vs 无监督学习
回归 vs 分类 Regression vs Classification
训练集 vs 测试集 vs 验证集
泛化和过拟合 Generalization & Overfitting
线性分类器 Linear Classifiers
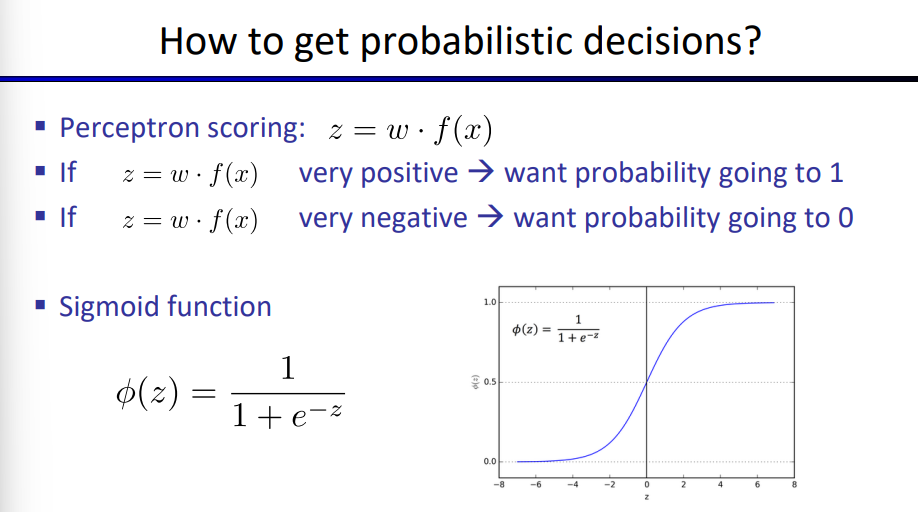
激活函数 - 概率决策
⚠线性回归
决策树 Decision Trees
决策树构建递归退出条件C
信息熵 Entropy
信息增益 Information Gain
⚠ID3算法实例
总结
前言
本复习笔记基于李晶晶老师的课堂PPT与复习大纲，供自己期末复习与学弟学妹参考用。
本节是人工智能复习的最后一小节，重点在于了解概念，会做计算题。
前面几节都在专栏当中，可以自行查看，也可以走传送门：
电子科技大学人工智能期末复习笔记（一）：搜索问题
电子科技大学人工智能期末复习笔记（二）：MDP与强化学习
电子科技大学人工智能期末复习笔记（三）：一阶逻辑
电子科技大学人工智能期末复习笔记（四）：概率与贝叶斯网络
监督学习 vs 无监督学习
监督学习：输入已知类别的数据样本 分类、回归
无监督学习：输入未知类别的数据样本 聚类
回归 vs 分类 Regression vs Classification
分类：对输入数据进行离散值标签的预测
回归：预测连续的、具体的数值
Output： 连续 vs 离散
分类需要激活函数
训练集 vs 测试集 vs 验证集
训练集用于学习参数（例如模型概率）
测试集用于计算模型的准确率
验证集用于调节超参数
泛化和过拟合 Generalization & Overfitting
在有监督学习中，我们会在训练数据集上建立一个模型，之后会把这个模型用于新的，之前从未见过的数据中，这个过程称为模型的泛化
模型在训练集上表现好，在测试集验证集表现差就说明出现了过拟合问题，出现这种情况的主要原因是训练数据中存在噪音或者训练数据太少
解决办法：选取合适的停止训练标准；使用验证数据集；获取额外数据进行交叉验证；正则化
Relative frequency parameters will overfit the training data
相对频率参数会过拟合训练数据
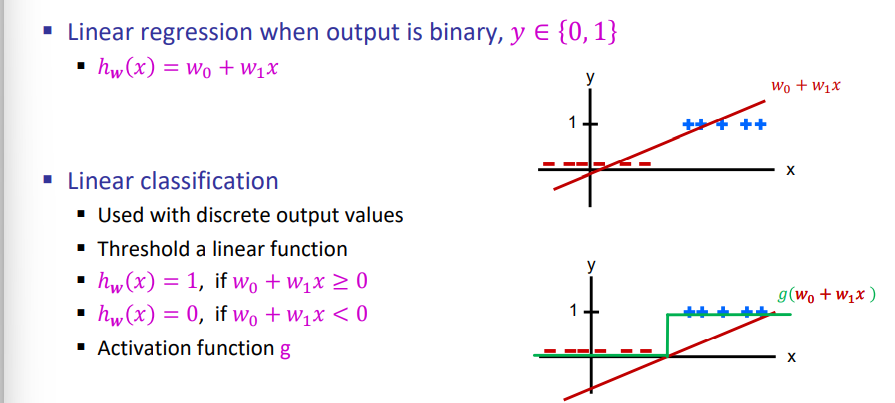
线性分类器 Linear Classifiers
输入特征向量 f(x)
权重向量 w
在二分类中：
真实标签为 y*∈{-1，1}，
预测标签为 y ，w和f(x)在同一平面则为正样本，y=1，反之y=-1
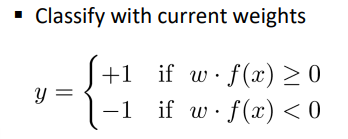
如果分类正确，不更新w，分类错误则更新 w
w = w + y* · f(x) 其中y* = 1或-1
在多分类中：
输入特征向量 f(x)
每个类别的权重 向量 
预测标签为 y ，取
最大的一个类别标签
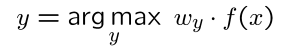
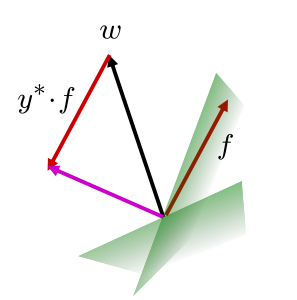
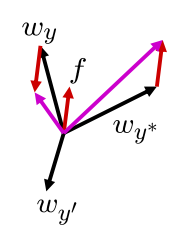
如果分类正确，不更新w；分类错误则更新 w，此时需要分别对正确和错误的两个w进行更新
关键点：减小错分类别的向量点积，增大真实类别的向量点积
激活函数 - 概率决策
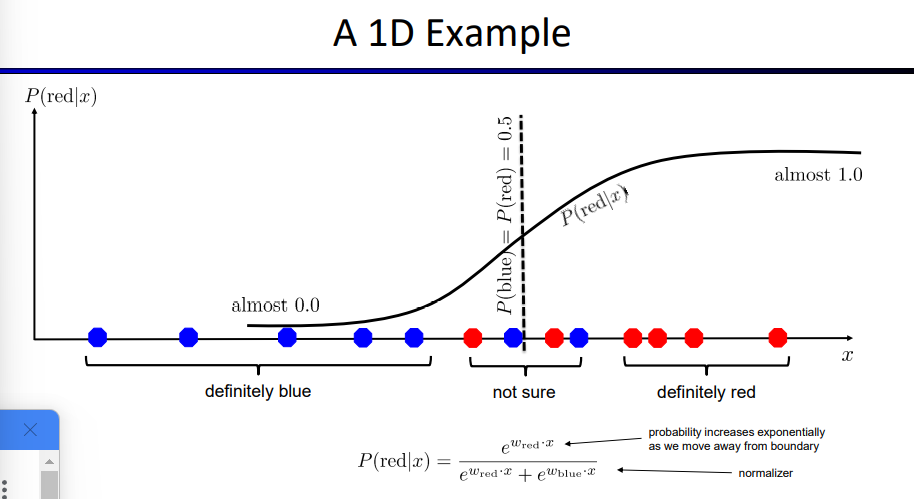
⚠线性回归
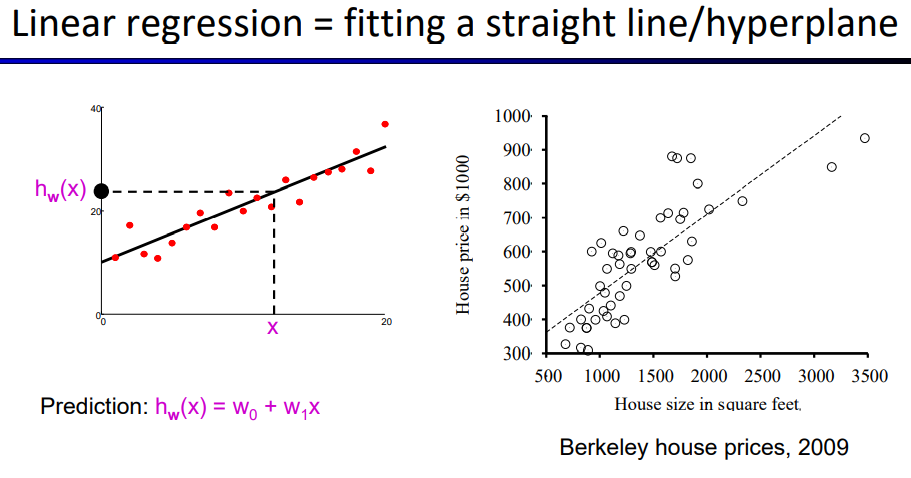
L2 loss：所有样本的平方误差和
例：
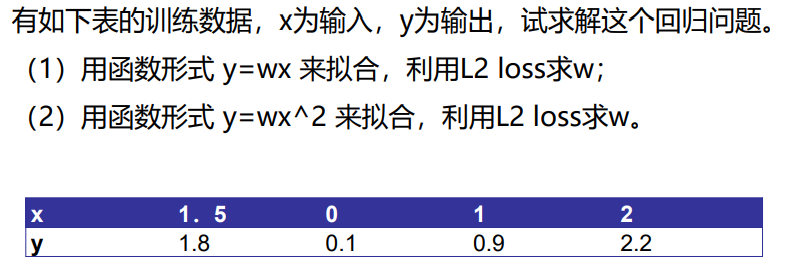
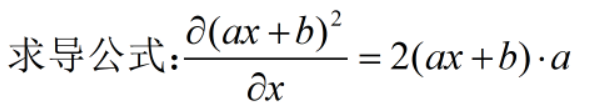
决策树 Decision Trees
决策树构建递归退出条件C
- 当前样本集D包含的样本属于同一类别C
- 当前属性集A为空或样本集D中所有样本在所有属性上取值相同（但类别可能不相同）
- 当前结点包含的样本集
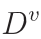为空
信息熵 Entropy
信息熵是度量样本集合纯度的指标
假定当前样本集合D中第k类样本所占比例为pk（k=1，2，...，|y|）则D的信息熵的定义为：
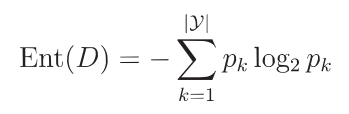
Ent(D)的取值范围为 [0,log2|y| ]，值越小，纯度越高
计算信息熵时约定：若p=0，则
=0
信息增益 Information Gain
样本集D的某个离散属性a有V个可能的取值
，用a来对D进行划分则会产生V个分支结点，其中第v个分支结点包含了D中所有在在属性a上取值为
的样本，记为
。定义用属性a对样本集D进行划分所获得的信息增益为：
一般而言，信息增益越大，意味着使用属性a来进行划分获得的纯度提升越大
在ID3算法中选择信息增益大的属性来划分样本集
⚠ID3算法实例
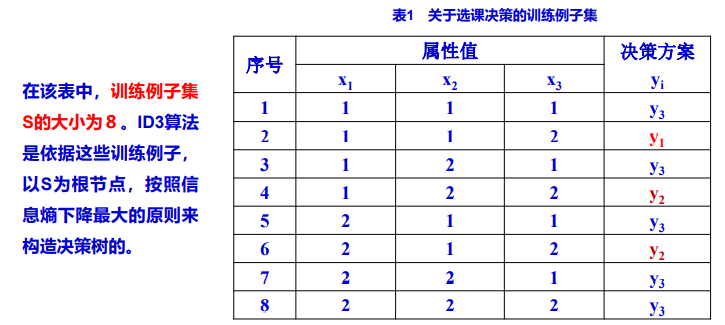
总结
至此人工智能复习笔记更新完毕，后续有时间会更新一下实验的讲解，包括基于A*算法的八数码问题求解、ID3决策树实战、以及Q-learning和Sarsa实现的悬崖问题求解。
