leetcode刷题 | 关于前缀和题型总结1

题目链接

560. 和为 K 的子数组 - 力扣（LeetCode）

525. 连续数组 - 力扣（LeetCode）

209. 长度最小的子数组 - 力扣（LeetCode）

437. 路径总和 III - 力扣（LeetCode）

和为K的子数组

前缀和：默认下标可以从1开始

前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和

class Solution {
    public int subarraySum(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();
        map.put(0,1);
        int[] sums = new int[nums.length+1];
        for(int i = 1;i<nums.length+1;i++){
            sums[i] = sums[i-1]+nums[i-1];
        }
        int res = 0;
        for(int i = 1;i<sums.length;i++){
            int target = sums[i]-k;
            res += map.getOrDefault(target,0);
            map.put(sums[i],map.getOrDefault(sums[i],0)+1);
        }
        return res;
    }
}

可以先计算出每一个元素的前缀和，本题求解的是和为k的子数组，也就是从下标[j,i]元素的和为k，这条件可以表示为sums[i]-sums[j-1] == k，，那么进行变换可以得到sums[i]-k == sums[j-1]，就可以转换为前缀和sums数组中有多少个值等于sum[i]-k

map保存的是以前缀和为键，出现的次数为值，通过从map中获取到sums[j-1]的个数

每一次循环都要将得到的前缀和存入到map中，以便下一次计算

之后的每一道题的思想都类似于本题

连续数组/0 和 1 个数相同的子数组

class Solution {
    public int findMaxLength(int[] nums) {
        int res = 0;
        int[] sums = new int[nums.length+1];
        for(int i = 1;i<sums.length;i++){
            sums[i] = sums[i-1]+(nums[i-1] == 0? -1 : 1);
        }
        Map<Integer,Integer> map = new HashMap();
        map.put(0,0);
        for(int i = 1;i<sums.length;i++){
            if(map.containsKey(sums[i])) res = Math.max(res,i-map.get(sums[i]));
            else map.put(sums[i],i);
        }
        return res;
    }
}

和大于等于 target 的最短子数组/长度最小的子数组

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int start = 0;
        int sum = 0;
        int res = Integer.MAX_VALUE;
        for(int i= 0; i< nums.length;i++){
            sum+=nums[i];
            while(sum >= target){
                res = Math.min(res,i-start+1);
                sum -= nums[start];
                start ++;
            }
            
        }
        return res == Integer.MAX_VALUE?0: res;
    }
}

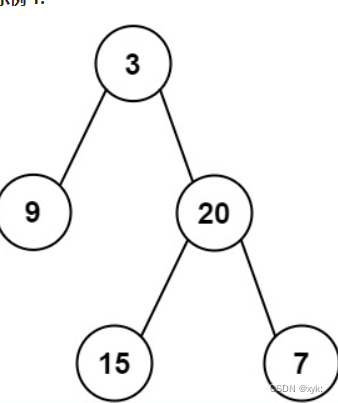
路经总和Ⅲ

前缀和解法

class Solution {
    public int pathSum(TreeNode root, long targetSum) {
        Map<Long, Integer> prefix = new HashMap<Long, Integer>();
        prefix.put(0L, 1);
        return dfs(root, prefix, 0, targetSum);
    }
    public int dfs(TreeNode root,Map<Long,Integer> prefix,long cur,long target){
        if (root == null) return 0;
        int res = 0;
        cur += root.val; //当前节点的前缀和
        res = prefix.getOrDefault(cur-target,0);
        prefix.put(cur,prefix.getOrDefault(cur,0)+1);
        res += dfs(root.left,prefix,cur,target);
        res += dfs(root.right,prefix,cur,target);
        //回溯
        prefix.put(cur,prefix.getOrDefault(cur,0)-1);
        return res;
    }
}

递归解法

class Solution {
   public int pathSum(TreeNode root, long targetSum) {
        if(root == null) return 0;
        int count = nodeSum(root, targetSum);
       // 每一个节点都作为根节点进行递归
        return count + pathSum(root.left, targetSum) + pathSum(root.right, targetSum);
    }
    private int nodeSum(TreeNode node, long targetSum){
        if(node == null) return 0;
        int count = 0;
        long val = node.val;
        if(val == targetSum) count++;
        return count + nodeSum(node.left, targetSum - val) + nodeSum(node.right, targetSum - val);
    }
}

targetSum) count++;
return count + nodeSum(node.left, targetSum - val) + nodeSum(node.right, targetSum - val);
}
}