1. 0-1背包问题理论基础(二维数组实现)

背包问题一般分为这几种：

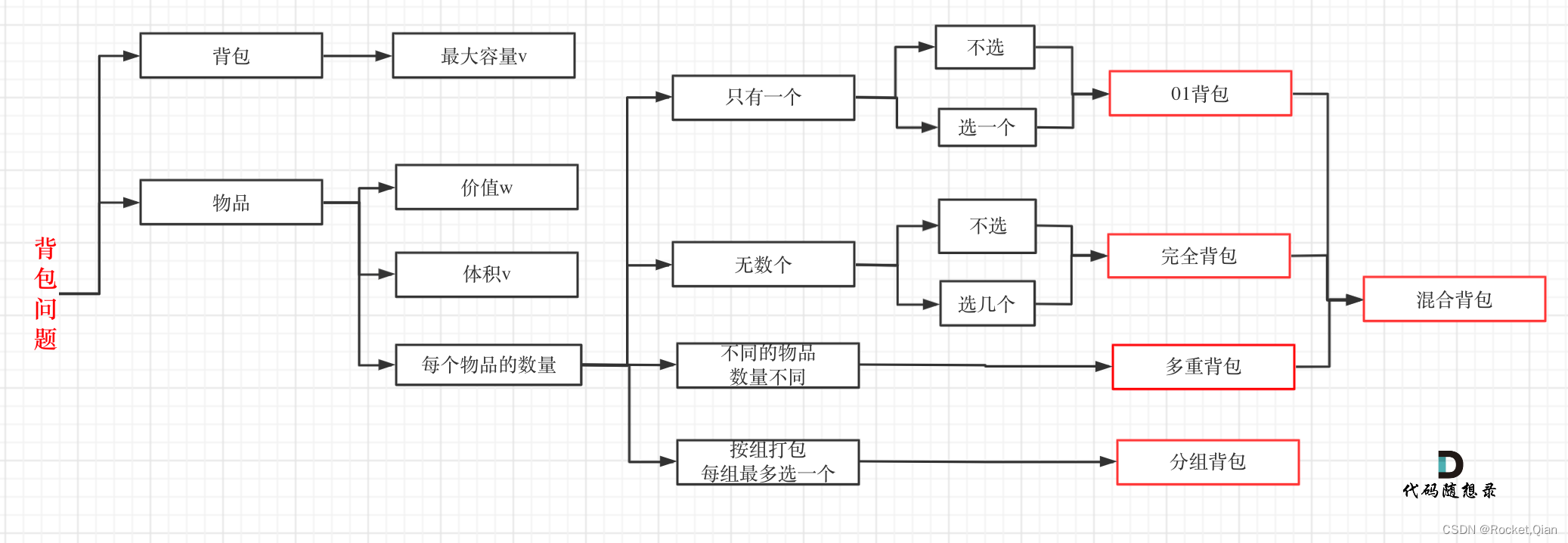
0-1背包问题：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

二维dp数组01背包

• 确定dp数组以及下标的含义
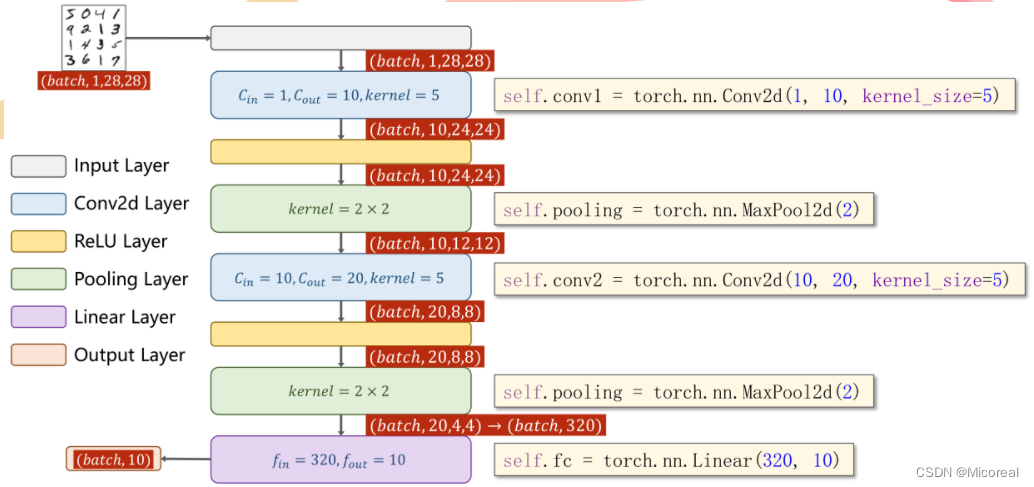
  对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
• 确定递推公式
  再回顾一下dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
  那么可以有两个方向推出来dp[i][j]，
  • 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)
  • 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
    所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
• dp数组如何初始化
• 确定遍历顺序 先遍历物品更好理解。
• 举例推导dp数组

def test_2_wei_bag_problem1(bag_size, weight, value) -> int: 
	rows, cols = len(weight), bag_size + 1
	dp = [[0 for _ in range(cols)] for _ in range(rows)]
    
	# 初始化dp数组. 
	for i in range(rows): 
		dp[i][0] = 0
	first_item_weight, first_item_value = weight[0], value[0]
	for j in range(1, cols): 	
		if first_item_weight <= j: 
			dp[0][j] = first_item_value

	# 更新dp数组: 先遍历物品, 再遍历背包. 
	for i in range(1, len(weight)): 
		cur_weight, cur_val = weight[i], value[i]
		for j in range(1, cols): 
			if cur_weight > j: # 说明背包装不下当前物品. 
				dp[i][j] = dp[i - 1][j] # 所以不装当前物品. 
			else: 
				# 定义dp数组: dp[i][j] 前i个物品里，放进容量为j的背包，价值总和最大是多少。
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight]+ cur_val)

	print(dp)


if __name__ == "__main__": 
	bag_size = 4
	weight = [1, 3, 4]
	value = [15, 20, 30]
	test_2_wei_bag_problem1(bag_size, weight, value)

2. 0-1背包问题理论基础 二（一维数组实现）

def test_1_wei_bag_problem():
    weight = [1, 3, 4]
    value = [15, 20, 30]
    bag_weight = 4
    # 初始化: 全为0
    dp = [0] * (bag_weight + 1)

    # 先遍历物品, 再遍历背包容量
    for i in range(len(weight)):
        for j in range(bag_weight, weight[i] - 1, -1):
            # 递归公式
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

    print(dp)

test_1_wei_bag_problem()

416. 分割等和子集

给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

只有确定了如下四点，才能把01背包问题套到本题上来。

• 背包的体积为sum / 2
• 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
• 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
• 背包中每一个元素是不可重复放入。
  以上分析完，我们就可以套用01背包，来解决这个问题了。

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        target = sum(nums)
        if target % 2 == 1: return False
        target //= 2
        dp = [0] * 10001
        for i in range(len(nums)):
            for j in range(target, nums[i] - 1, -1):
                dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
        return target == dp[target]