题目：

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

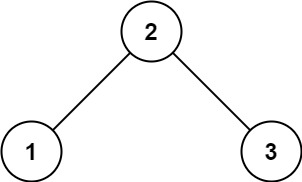
输入：root = [2,1,3]
输出：true

示例 2：

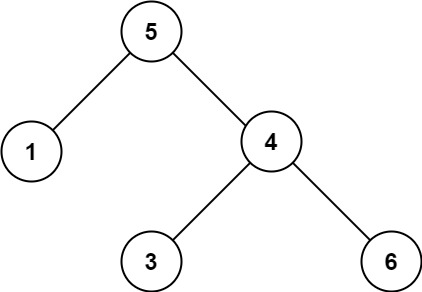
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

---

思路：

要注意某个结点的左右孩子不仅仅是要满足对于自己的双亲的大小，对于双亲的双亲也要满足。

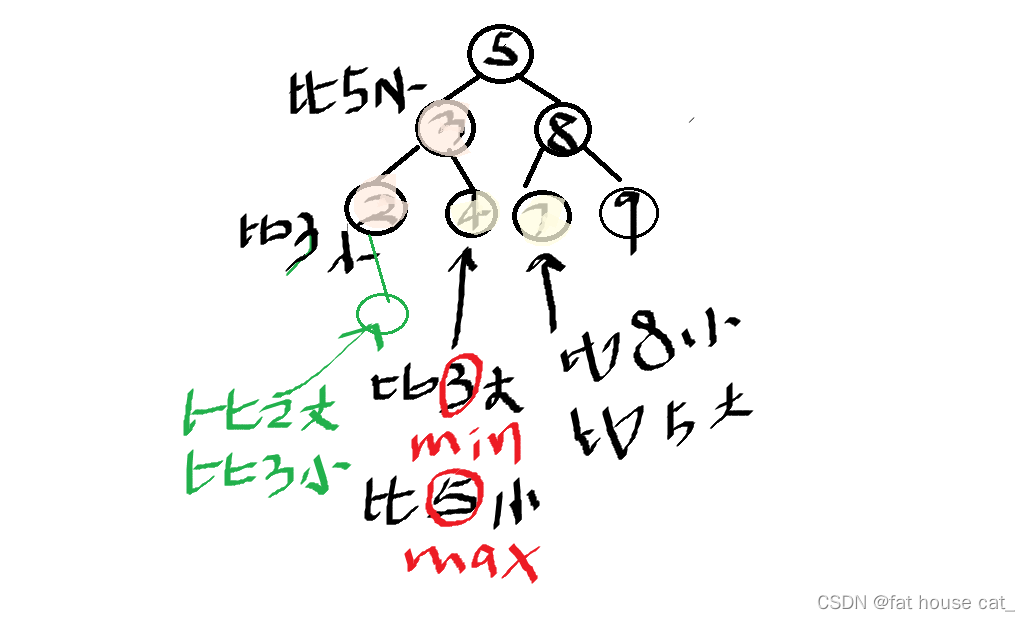
所以就会想到在递归的时候设置最大最小值。每个结点都应满足大于最小值小于最小值。

那对于每个结点要怎么去确定这个最大最小值呢？

对于左孩子，总是要比双亲小，所以递归左节点时，最大值要一起更新，最大值就是这个双亲的值。 最小值不用更新。用现有的最小值即可。

对于右孩子，总要比双亲大，所以递归右结点时，最小值要一起更新。同里最大值不用更新。比如当root->val==3时，此时还跟着max=5。所以当进入root->right时，max不用更新。

---

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isValid(struct TreeNode* root,long min,long max){
    if(root==NULL){
        return true;
    }
    if(root->val<=min||root->val>=max){
        return false;
    } 
    return isValid(root->left,min,root->val)&&isValid(root->right,root->val,max);
}
bool isValidBST(struct TreeNode* root){
    if(root==NULL){
        return true;
    }
    return isValid(root,LONG_MIN,LONG_MAX);
}

---

学到的：1.LONG_MAX 存在与头文件limits.h中，表示long int 类型的最大值。

               2.&&

① 当逻辑与左边为false(假)，则不再进行逻辑与右边的判断，结果为false(假)
② 当逻辑与左边为true(真)则进行右边判断，右边为false(假)，结果为false(假)
③ 当逻辑与左边为true(真)则进行右边判断，右边也为true(真)，则结果为true(真)

               3.min，max参与递归的思路