110.平衡二叉树

力扣题目链接

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

 

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

 返回 false 。

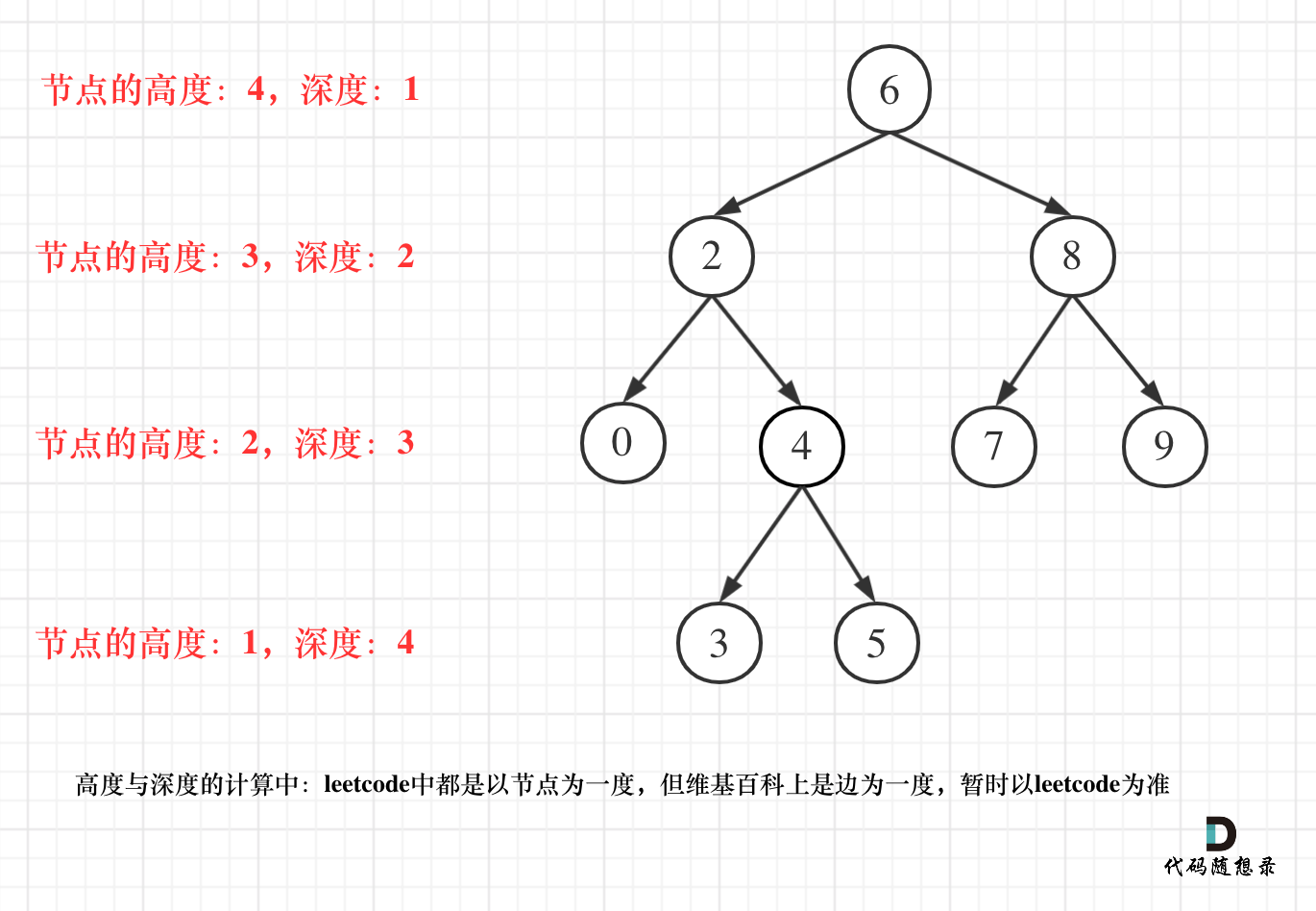
• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

但leetcode中强调的深度和高度很明显是按照节点来计算的，如图：

 

var isBalanced=function(root){
    if(root===null) return true;
    if(Math.abs(getHeight(root.left)-getHeight(root.right))>1) return false;
    return isBalanced(root.left)&&isBalanced(root.right);
}
var getHeight=function(root){
    if(root===null) return 0;
    return Math.max(getHeight(root.left),getHeight(root.right))+1;
}
// 代码随想录
// 递归法：
var isBalanced = function(root) {
    //还是用递归三部曲 + 后序遍历 左右中 当前左子树右子树高度相差大于1就返回-1
    // 1. 确定递归函数参数以及返回值
    const getDepth = function(node) {
        // 2. 确定递归函数终止条件
        if(node === null) return 0;
        // 3. 确定单层递归逻辑
        let leftDepth = getDepth(node.left); //左子树高度
        // 当判定左子树不为平衡二叉树时,即可直接返回-1
        if(leftDepth === -1) return -1;
        let rightDepth = getDepth(node.right); //右子树高度
        // 当判定右子树不为平衡二叉树时,即可直接返回-1
        if(rightDepth === -1) return -1;
        if(Math.abs(leftDepth - rightDepth) > 1) {
            return -1;
        } else {
            return 1 + Math.max(leftDepth, rightDepth);
        }
    }
    return !(getDepth(root) === -1);
};
// 迭代法：
// 获取当前节点的高度
//getHeight函数的作用是获取当前节点的高度
var getHeight = function (curNode) {
    let queue = [];
    if (curNode !== null) queue.push(curNode); // 压入当前元素
    let depth = 0, res = 0;
    while (queue.length) {
        let node = queue[queue.length - 1]; // 取出栈顶
        if (node !== null) {
            queue.pop();
            queue.push(node);   // 中
            queue.push(null);
            depth++;
            node.right && queue.push(node.right);   // 右
            node.left && queue.push(node.left);     // 左
        } else {
            queue.pop();
            node = queue[queue.length - 1];
            queue.pop();
            depth--;
        }
        res = res > depth ? res : depth;
    }
    return res;
}
var isBalanced = function (root) {
    if (root === null) return true;
    let queue = [root];
    while (queue.length) {
        let node = queue[queue.length - 1]; // 取出栈顶
        queue.pop();    
        if (Math.abs(getHeight(node.left) - getHeight(node.right)) > 1) {
            return false;
        }
        node.right && queue.push(node.right);
        node.left && queue.push(node.left);
    }
    return true;
};

257. 二叉树的所有路径

力扣题目链接(opens new window)

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

 

 

var binaryTreePaths = function(root) {
    if(root===null) return [];
    if(root.left===null&&root.right===null) return [root.val.toString()];
    let left_paths=binaryTreePaths(root.left);
    let right_paths=binaryTreePaths(root.right);
    let paths=[];
    for(let path of left_paths){
        paths.push(root.val.toString()+"->"+path);
    }
    for(let path of right_paths){
        paths.push(root.val.toString()+"->"+path);
    }
    return paths;
}
// 代码随想录
// 递归法
var binaryTreePaths = function(root) {
    //递归遍历+递归三部曲
    let res = [];
    //1. 确定递归函数 函数参数
    const getPath = function(node,curPath) {
     //2. 确定终止条件，到叶子节点就终止
        if(node.left === null && node.right === null) {
            curPath += node.val;
            res.push(curPath);
            return;
        }
        //3. 确定单层递归逻辑
        curPath += node.val + '->';
        node.left && getPath(node.left, curPath);
        node.right && getPath(node.right, curPath);
    }
    getPath(root, '');
    return res;
 };
//  迭代法：
var binaryTreePaths = function(root) {
    if (!root) return [];
    const stack = [root], paths = [''], res = [];
    while (stack.length) {
      const node = stack.pop();
      let path = paths.pop();
      if (!node.left && !node.right) { // 到叶子节点终止, 添加路径到结果中
        res.push(path + node.val);
        continue;
      }
      path += node.val + '->';
      if (node.right) { // 右节点存在
        stack.push(node.right);
        paths.push(path);
      }
      if (node.left) { // 左节点存在
        stack.push(node.left);
        paths.push(path);
      }
    }
    return res;
  };  

• #404.左叶子之和

  力扣题目链接

var sumOfLeftLeaves=function(root){
    if(root===null) return 0;
    let sum=0;
    if(root.left!==null&&root.left.left===null&&root.left.right===null){
        sum+=root.left.val;
    }
    sum+=sumOfLeftLeaves(root.left);
    sum+=sumOfLeftLeaves(root.right);
    return sum;
}
// 代码随想录
// 递归法
var sumOfLeftLeaves = function(root) {
    //采用后序遍历 递归遍历
    // 1. 确定递归函数参数
    const nodesSum = function(node) {
        // 2. 确定终止条件
        if(node === null) {
            return 0;
        }
        let leftValue = nodesSum(node.left);
        let rightValue = nodesSum(node.right);
        // 3. 单层递归逻辑
        let midValue = 0;
        if(node.left && node.left.left === null && node.left.right === null) {
            midValue = node.left.val;
        }
        let sum = midValue + leftValue + rightValue;
        return sum;
    }
    return nodesSum(root);
};
// 迭代法
var sumOfLeftLeaves = function(root) {
    //采用层序遍历
    if(root === null) {
        return null;
    }
    let queue = [];
    let sum = 0;
    queue.push(root);
    while(queue.length) {
      let node = queue.shift();
      if(node.left !== null && node.left.left === null && node.left.right === null) {
          sum+=node.left.val;
      }
      node.left && queue.push(node.left);
      node.right && queue.push(node.right);
    }
    return sum;
 };