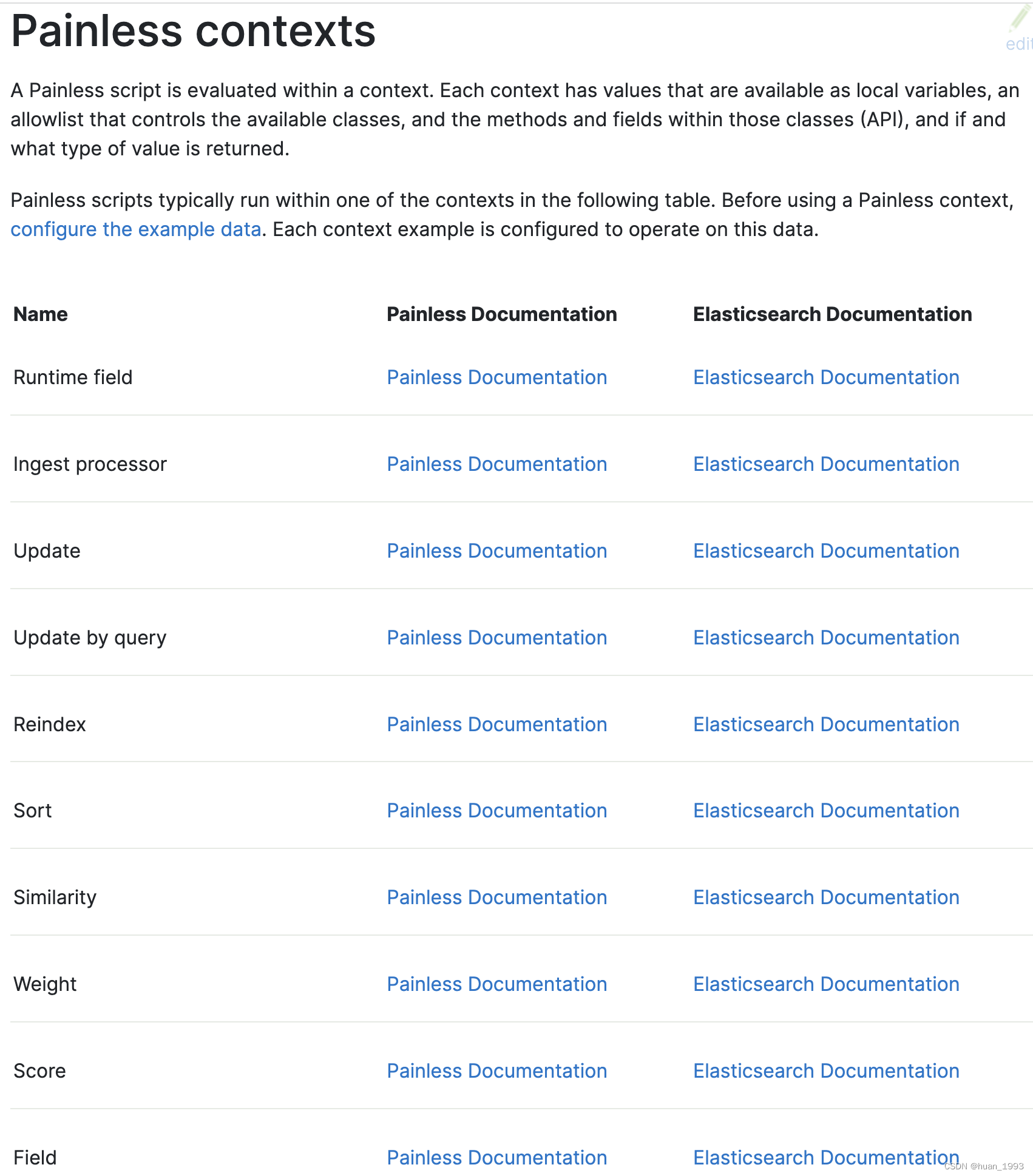
C++与Lua交互实例 – 矩阵的加减乘除(版本一)
关于lua中封装的类模板以及相关知识可参考以下链接:
https://ufgnix0802.blog.csdn.net/article/details/128854786
https://ufgnix0802.blog.csdn.net/article/details/128827673
https://ufgnix0802.blog.csdn.net/article/details/128827618
该案例的主要目的是使用矩阵的加减乘除这个功能来练习C++与Lua之间的交互(针对性地说就是熟练使用C++与Lua之间的交互API以及深刻理解lua堆栈的原理)。
在这个过程中,CppToLua表示矩阵的数据来源于C++端,然后让Lua使用Lua的矩阵运算逻辑进行计算并返回结果给C++端。C++端使用自己定义的C++矩阵类进行本地矩阵运算,然后与lua端返回的矩阵运算结果进行比对展示。
LuaToCpp同理,与CppToLua相反。表示矩阵的数据来源于lua端,然后调用C++端暴露给Lua端的API创建C++矩阵类实例,并进行矩阵运算。lua端本地使用lua端的类构建矩阵table,并进行本地运算,然后使用运算结果与C++端API的运算结果进行比对展示。
Matrix.hpp
该部分封装C++端Matrix类,下面两个调用方式都有进行实际应用。
#pragma once
#include <iostream>
#include <vector>
typedef std::vector<double> vec;
typedef std::vector<vec> matrixData;
class Matrix {
public:
Matrix() { }
~Matrix() { }
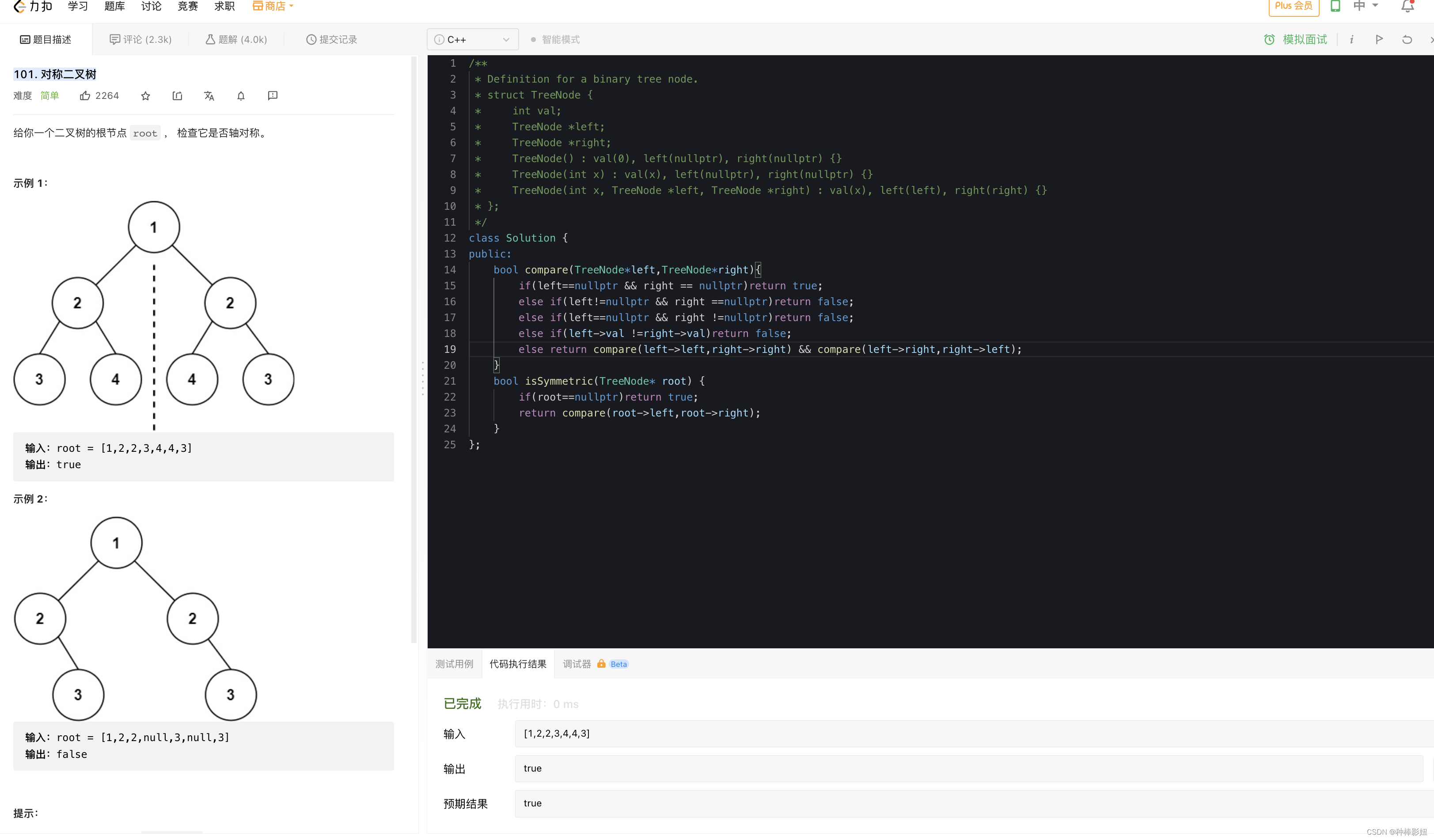
bool Init(const std::vector<std::vector<double>>& data) {
m_data.assign(data.begin(), data.end());
m_row = m_data.size();
if (m_row > 0) {
m_column = m_data[0].size();
}
else {
m_column = 0;
}
return true;
}
bool UnInit() {
m_row = 0;
m_column = 0;
m_data.clear();
return true;
}
Matrix(const Matrix& matrix) {
Init(matrix.m_data);
}
Matrix operator+(const Matrix& matrix) {
Matrix res;
if (this->m_row != matrix.m_row ||
this->m_column != matrix.m_column) {
return res;
}
std::vector<std::vector<double>> data(m_row,
std::vector<double>(m_column, 0));
for (int32_t i = 0; i < m_row; i++) {
for (int32_t j = 0; j < m_column; j++) {
data[i][j] = this->m_data[i][j] + matrix.m_data[i][j];
}
}
res.Init(data);
return res;
}
Matrix operator-(const Matrix& matrix) {
Matrix res;
if (this->m_row != matrix.m_row ||
this->m_column != matrix.m_column) {
return res;
}
std::vector<std::vector<double>> data(m_row,
std::vector<double>(m_column, 0));
for (int32_t i = 0; i < m_row; i++) {
for (int32_t j = 0; j < m_column; j++) {
data[i][j] = this->m_data[i][j] - matrix.m_data[i][j];
}
}
res.Init(data);
return res;
}
Matrix operator*(const Matrix& matrix) {
Matrix res;
if (this->m_column != matrix.m_row) {
return res;
}
res.Init(_MatrixMul(matrix.m_data));
return res;
}
Matrix operator/(const Matrix& matrix) {
Matrix res;
double nDetRet = _GetDetValue(matrix.m_data);
if (0 == nDetRet) {
return res;
}
matrixData data = _GetCompanyMatrix(matrix.m_data);
_NumMul(data, 1 / nDetRet);
res.Init(_MatrixMul(data));
return res;
}
void Print() {
for (int i = 0; i < m_row; i++) {
for (int j = 0; j < m_column; j++)
printf("%lf ", m_data[i][j]);
std::cout << '\n';
}
std::cout << "......\n";
}
private:
matrixData _MatrixMul(const matrixData& destMatrixData) {
std::vector<std::vector<double>> data(this->m_row,
std::vector<double>(destMatrixData[0].size(), 0));
for (int32_t i = 0; i < this->m_row; i++) {
for (int32_t j = 0; j < destMatrixData[0].size(); j++) {
for (int32_t k = 0; k < this->m_column; k++) {
data[i][j] += (m_data[i][k] * destMatrixData[k][j]);
}
}
}
return data;
}
matrixData _CutoffMatrix(const matrixData& data,
int32_t rowIndex, int32_t colIndex) {
int32_t row = data.size() - 1;
int32_t col = data[0].size() - 1;
matrixData res(row, vec(col, 0));
for (int32_t i = 0; i < row; i++) {
for (int32_t j = 0; j < col; j++) {
res[i][j] =
data[i + (i >= rowIndex)][j + (j >= colIndex)];
}
}
return res;
}
double _GetDetValue(const matrixData& data) {
if (1 == data.size()) {
return data[0][0];
}
double ans = 0;
for (int32_t i = 0; i < data[0].size(); i++) {
ans += data[0][i] * _GetDetValue(_CutoffMatrix(data, 0, i))
* (i % 2 ? -1 : 1);
}
return ans;
}
matrixData _GetCompanyMatrix(const matrixData& data) {
int32_t row = data.size();
int32_t col = data[0].size();
matrixData res(col, vec(row));
for (int32_t i = 0; i < row; i++) {
for (int32_t j = 0; j < col; j++) {
res[j][i] = _GetDetValue(_CutoffMatrix(data, i, j))
* ((i + j) % 2 ? -1 : 1);
}
}
return res;
}
bool _NumMul(matrixData& putOutData, double num) {
for (int i = 0; i < putOutData.size(); i++)
for (int j = 0; j < putOutData[0].size(); j++)
putOutData[i][j] = putOutData[i][j] * num;
return true;
}
private:
int32_t m_row;
int32_t m_column;
std::vector<std::vector<double>> m_data;
};
CppToLua
CppToLua.cpp
#include <iostream>
#include <vector>
#include "lua.hpp"
#include "Matrix.hpp"
// 在Lua中创建Matrix对象
bool CreateLuaMatrixObj(lua_State* const L,
const std::vector<std::vector<double>>& data, const char* name) {
bool result = false;
int top;
/*top = lua_gettop(L);
std::cout << "stack top:" << top << std::endl;*/
if (LUA_TFUNCTION != lua_getfield(L, -1, "New")) {
goto Exit;
}
//创建表
lua_newtable(L);
for (int32_t i = 0; i < data.size(); i++) {
lua_newtable(L);
for (int32_t j = 0; j < data[0].size(); j++) {
lua_pushnumber(L, data[i][j]);
lua_rawseti(L, -2, j + 1);
}
lua_rawseti(L, -2, i + 1);
}
//调用New方法
if (lua_pcall(L, 1, 1, 0)) {
printf("error[%s]\n", lua_tostring(L, -1));
goto Exit;
}
if (LUA_TTABLE != lua_type(L, -1)) {
goto Exit;
}
//需要使用一个全局变量保存起来
lua_setglobal(L, name);
/*top = lua_gettop(L);
std::cout << "stack top:" << top << std::endl;*/
result = true;
Exit:
return result;
}
// 矩阵运算
enum class MATRIX_OPERATE {
ADD,
SUB,
MUL,
DIV,
NONE
};
// 使用Lua中的两个Matrix对象相加,并获取相加结果
bool MatrixOperate(lua_State* const L,
const char* matrix1Name, const char* matrix2Name,
std::vector<std::vector<double>>& outRes, MATRIX_OPERATE type) {
bool result = false;
int top;
int32_t row = 0;
int32_t col = 0;
const char* operate = NULL;
switch (type) {
case MATRIX_OPERATE::ADD:
operate = "Add";
break;
case MATRIX_OPERATE::SUB:
operate = "Sub";
break;
case MATRIX_OPERATE::MUL:
operate = "Mul";
break;
case MATRIX_OPERATE::DIV:
operate = "Div";
break;
case MATRIX_OPERATE::NONE:
break;
default:
break;
}
lua_getglobal(L, matrix1Name);
if (LUA_TFUNCTION != lua_getfield(L, -1, operate)) {
goto Exit;
}
//top = 3
/*top = lua_gettop(L);
std::cout << "--- stack top:" << top << std::endl;*/
lua_getglobal(L, matrix1Name);
lua_getglobal(L, matrix2Name);
//top = 5
/*top = lua_gettop(L);
std::cout << "stack top:" << top << std::endl;*/
//调用矩阵运算方法
if (lua_pcall(L, 2, 1, 0)) {
printf("error[%s]\n", lua_tostring(L, -1));
goto Exit;
}
//top = 3
/*top = lua_gettop(L);
std::cout << "222 stack top:" << top << std::endl;*/
luaL_checktype(L, -1, LUA_TTABLE);
if (LUA_TTABLE != lua_getfield(L, -1, "tbData")) {
goto Exit;
}
//top = 4
luaL_checktype(L, -1, LUA_TTABLE);
/*top = lua_gettop(L);
std::cout << "stack top:" << top << std::endl;*/
lua_getfield(L, -2, "nRow");
/*top = lua_gettop(L);
std::cout << "stack top:" << top << std::endl;*/
row = lua_tointeger(L, -1);
lua_pop(L, 1);
lua_getfield(L, -2, "nColumn");
/*top = lua_gettop(L);
std::cout << "stack top:" << top << std::endl;*/
col = lua_tointeger(L, -1);
lua_pop(L, 1);
//top = 4
/*top = lua_gettop(L);
std::cout << "stack top:" << top << std::endl;*/
for (int32_t i = 0; i < row; i++) {
lua_rawgeti(L, -1, i + 1);
std::vector<double> data;
for (int32_t j = 0; j < col; j++) {
lua_rawgeti(L, -1, j + 1);
data.push_back(lua_tonumber(L, -1));
lua_pop(L, 1);
}
outRes.push_back(data);
lua_pop(L, 1);
}
// lua堆栈平衡
lua_pop(L, 3);
// top = 1
/*top = lua_gettop(L);
std::cout << "stack top:" << top << std::endl;*/
result = true;
Exit:
return result;
}
int main() {
lua_State* L = luaL_newstate();
luaL_openlibs(L);
std::vector<std::vector<double>> luaMat1 = { { 1,2,3 }, { 4,5,6 } };
std::vector<std::vector<double>> luaMat2 = { { 2,3,4 }, { 5,6,7 } };
std::vector<std::vector<double>> luaMat3 = { {1,2,3},{4,5,6} };
std::vector<std::vector<double>> luaMat4 = { {7,8},{9,10},{11,12} };
std::vector<std::vector<double>> luaMat5 = { {1,2,3},{4,5,6},{7,8,0} };
std::vector<std::vector<double>> luaMat6 = { {1,2,1},{1,1,2},{2,1,1} };
if (luaL_dofile(L, "matrix2.0.lua")) {
printf("%s\n", lua_tostring(L, -1));
}
lua_getglobal(L, "Matrix");
luaL_checktype(L, -1, LUA_TTABLE);
//C++ -》 lua 及 lua -》 C++
CreateLuaMatrixObj(L, luaMat1, "mat1");
CreateLuaMatrixObj(L, luaMat2, "mat2");
std::cout <<
"----------------------------加法运算结果:----------------------------"
<< std::endl;
std::vector<std::vector<double>> addRes;
MatrixOperate(L, "mat1", "mat2", addRes, MATRIX_OPERATE::ADD);
Matrix mat1;
mat1.Init(luaMat1);
Matrix mat2;
mat2.Init(luaMat2);
Matrix mat3;
mat3 = mat1 + mat2;
std::cout << "lua运算结果:" << std::endl;
for (int i = 0; i < addRes.size(); i++) {
for (int j = 0; j < addRes[0].size(); j++)
printf("%lf ", addRes[i][j]);
std::cout << '\n';
}
std::cout << "......\n";
std::cout << "C++运算结果:" << std::endl;
mat3.Print();
std::cout <<
"----------------------------减法运算结果:----------------------------"
<< std::endl;
std::vector<std::vector<double>> subRes;
MatrixOperate(L, "mat1", "mat2", subRes, MATRIX_OPERATE::SUB);
Matrix mat4;
mat4 = mat1 - mat2;
std::cout << "lua运算结果:" << std::endl;
for (int i = 0; i < subRes.size(); i++) {
for (int j = 0; j < subRes[0].size(); j++)
printf("%lf ", subRes[i][j]);
std::cout << '\n';
}
std::cout << "......\n";
std::cout << "C++运算结果:" << std::endl;
mat4.Print();
std::cout <<
"----------------------------乘法运算结果:----------------------------"
<< std::endl;
CreateLuaMatrixObj(L, luaMat3, "mat3");
CreateLuaMatrixObj(L, luaMat4, "mat4");
std::vector<std::vector<double>> mulRes;
MatrixOperate(L, "mat3", "mat4", mulRes, MATRIX_OPERATE::MUL);
Matrix mat5;
mat5.Init(luaMat3);
Matrix mat6;
mat6.Init(luaMat4);
Matrix mat7;
mat7 = mat5 * mat6;
std::cout << "lua运算结果:" << std::endl;
for (int i = 0; i < mulRes.size(); i++) {
for (int j = 0; j < mulRes[0].size(); j++)
printf("%lf ", mulRes[i][j]);
std::cout << '\n';
}
std::cout << "......\n";
std::cout << "C++运算结果:" << std::endl;
mat7.Print();
std::cout <<
"----------------------------除法运算结果:----------------------------"
<< std::endl;
CreateLuaMatrixObj(L, luaMat5, "mat5");
CreateLuaMatrixObj(L, luaMat6, "mat6");
std::vector<std::vector<double>> divRes;
if (!MatrixOperate(L, "mat5", "mat6", divRes, MATRIX_OPERATE::DIV)) {
std::cout << "无法进行矩阵的除法" << std::endl;
}
Matrix mat8;
mat8.Init(luaMat5);
Matrix mat9;
mat9.Init(luaMat6);
mat9 = mat8 / mat9;
std::cout << "lua运算结果:" << std::endl;
for (int i = 0; i < divRes.size(); i++) {
for (int j = 0; j < divRes[0].size(); j++)
printf("%lf ", divRes[i][j]);
std::cout << '\n';
}
std::cout << "......\n";
std::cout << "C++运算结果:" << std::endl;
mat9.Print();
lua_close(L);
system("pause");
return 0;
}
matrix2.0.lua
local _class = {}
function class(super)
local tbClassType = {}
tbClassType.Ctor = false
tbClassType.super = super
tbClassType.New = function(...)
local tbObj = {}
do
local funcCreate
funcCreate = function(tbClass,...)
if tbClass.super then
funcCreate(tbClass.super,...)
end
if tbClass.Ctor then
tbClass.Ctor(tbObj,...)
end
end
funcCreate(tbClassType,...)
end
-- 防止调用Ctor初始化时,在Ctor内部设置了元表的情况发生
if getmetatable(tbObj) then
getmetatable(tbObj).__index = _class[tbClassType]
else
setmetatable(tbObj, { __index = _class[tbClassType] })
end
return tbObj
end
local vtbl = {}
_class[tbClassType] = vtbl
setmetatable(tbClassType, { __newindex =
function(tb,k,v)
vtbl[k] = v
end
})
if super then
setmetatable(vtbl, { __index =
function(tb,k)
local varRet = _class[super][k]
vtbl[k] = varRet
return varRet
end
})
end
return tbClassType
end
Matrix = class()
function Matrix:Ctor(data)
self.tbData = data
self.nRow = #data
if self.nRow > 0 then
self.nColumn = (#data[1])
else
self.nColumn = 0
end
-- print("row:",self.nRow," col:",self.nColumn)
setmetatable(self,{
__add = function(tbSource, tbDest)
assert(tbSource,"tbSource not exist")
assert(tbDest, "tbDest not exist")
local tbRes = Matrix.New({})
-- print(tbSource,tbDest)
-- print("tbSource:",tbSource.nRow,tbSource.nColumn)
-- tbSource:Print()
-- print("tbDest:",tbDest.nRow,tbDest.nColumn)
-- tbDest:Print()
if tbSource.nRow ~= tbDest.nRow
or tbSource.nColumn ~= tbDest.nColumn then
print("row or column not equal...")
return tbRes
else
for rowKey,rowValue in ipairs(tbSource.tbData) do
for colKey,colValue in ipairs(tbSource.tbData[rowKey]) do
if tbRes.tbData[rowKey] == nil then
tbRes.tbData[rowKey] = {}
end
if tbRes.tbData[rowKey][colKey] == nil then
tbRes.tbData[rowKey][colKey] = 0
end
tbRes.tbData[rowKey][colKey] =
tbSource.tbData[rowKey][colKey] + tbDest.tbData[rowKey][colKey]
end
end
tbRes.nRow = tbSource.nRow
tbRes.nColumn = tbSource.nColumn
return tbRes
end
end,
__sub = function(tbSource, tbDest)
assert(tbSource,"tbSource not exist")
assert(tbDest, "tbDest not exist")
local tbRes = Matrix.New({})
if tbSource.nRow ~= tbDest.nRow
or tbSource.nColumn ~= tbDest.nColumn then
print("row or column not equal...")
return tbRes
else
for rowKey,rowValue in ipairs(tbSource.tbData) do
for colKey,colValue in ipairs(tbSource.tbData[rowKey]) do
if tbRes.tbData[rowKey] == nil then
tbRes.tbData[rowKey] = {}
end
if tbRes.tbData[rowKey][colKey] == nil then
tbRes.tbData[rowKey][colKey] = 0
end
tbRes.tbData[rowKey][colKey] =
tbSource.tbData[rowKey][colKey] - tbDest.tbData[rowKey][colKey]
end
end
tbRes.nRow = tbSource.nRow
tbRes.nColumn = tbSource.nColumn
return tbRes
end
end,
__mul = function(tbSource, tbDest)
return self:_MartixMul(tbSource, tbDest)
end,
__div = function(tbSource, tbDest)
assert(tbSource,"tbSource not exist")
assert(tbDest, "tbDest not exist")
local nDet = self:_GetDetValue(tbDest)
if nDet == 0 then
print("matrix no inverse matrix...")
return nil
end
-- print("det ",nDet)
local tbInverseDest = self:_MatrixNumMul(self:_GetCompanyMatrix(tbDest), 1 / nDet)
-- self:_GetCompanyMatrix(tbDest):Print()
-- print(nDet)
tbInverseDest:Print()
return self:_MartixMul(tbSource, tbInverseDest)
end
}
)
end
function Matrix:Print()
for rowKey,rowValue in ipairs(self.tbData) do
for colKey,colValue in ipairs(self.tbData[rowKey]) do
io.write(self.tbData[rowKey][colKey],',')
end
print('')
end
end
-- 加
function Matrix:Add(matrix)
return self + matrix
end
-- 减
function Matrix:Sub(matrix)
return self - matrix
end
-- 乘
function Matrix:Mul(matrix)
return self * matrix
end
-- 除
function Matrix:Div(matrix)
return self / matrix
end
-- 切割,切去第rowIndex以及第colIndex列
function Matrix:_CutoffMatrix(tbMatrix, rowIndex, colIndex)
assert(tbMatrix,"tbMatrix not exist")
assert(rowIndex >= 1,"rowIndex < 1")
assert(colIndex >= 1,"colIndex < 1")
local tbRes = Matrix.New({})
tbRes.nRow = tbMatrix.nRow - 1
tbRes.nColumn = tbMatrix.nColumn - 1
for i = 1, tbMatrix.nRow - 1 do
for j = 1, tbMatrix.nColumn - 1 do
if tbRes.tbData[i] == nil then
tbRes.tbData[i] = {}
end
local nRowDir = 0
local nColDir = 0
if i >= rowIndex then
nRowDir = 1
end
if j >= colIndex then
nColDir = 1
end
tbRes.tbData[i][j] = tbMatrix.tbData[i + nRowDir][j + nColDir]
end
end
return tbRes
end
-- 获取矩阵的行列式对应的值
function Matrix:_GetDetValue(tbMatrix)
assert(tbMatrix,"tbMatrix not exist")
-- 当矩阵为一阶矩阵时,直接返回A中唯一的元素
if tbMatrix.nRow == 1 then
return tbMatrix.tbData[1][1]
end
local nAns = 0
for i = 1, tbMatrix.nColumn do
local nFlag = -1
if i % 2 ~= 0 then
nFlag = 1
end
nAns =
nAns + tbMatrix.tbData[1][i] *
self:_GetDetValue(self:_CutoffMatrix(tbMatrix, 1, i)) * nFlag
-- print("_GetDetValue nflag:",nFlag)
end
return nAns
end
-- 获取矩阵的伴随矩阵
function Matrix:_GetCompanyMatrix(tbMatrix)
assert(tbMatrix,"tbMatrix not exist")
local tbRes = Matrix.New({})
-- 伴随矩阵与原矩阵存在转置关系
tbRes.nRow = tbMatrix.nColumn
tbRes.nColumn = tbMatrix.nRow
for i = 1, tbMatrix.nRow do
for j = 1, tbMatrix.nColumn do
local nFlag = 1
if ((i + j) % 2) ~= 0 then
nFlag = -1
end
if tbRes.tbData[j] == nil then
tbRes.tbData[j] = {}
end
-- print(Matrix:_GetDetValue(Matrix:_CutoffMatrix(tbMatrix, i, j)))
-- Matrix:_CutoffMatrix(tbMatrix, i, j):Print()
-- print("---11----")
tbRes.tbData[j][i] =
self:_GetDetValue(self:_CutoffMatrix(tbMatrix, i, j)) * nFlag
end
end
return tbRes
end
-- 矩阵数乘
function Matrix:_MatrixNumMul(tbMatrix, num)
for i = 1, tbMatrix.nRow do
for j = 1, tbMatrix.nColumn do
tbMatrix.tbData[i][j] = tbMatrix.tbData[i][j] * num
end
end
return tbMatrix
end
-- 矩阵相乘
function Matrix:_MartixMul(tbSource, tbDest)
assert(tbSource,"tbSource not exist")
assert(tbDest, "tbDest not exist")
if tbSource.nColumn ~= tbDest.nRow then
print("column not equal row...")
return tbSource
else
local tbRes = Matrix.New({})
for i = 1, tbSource.nRow do
for j = 1, tbDest.nColumn do
if tbRes.tbData[i] == nil then
tbRes.tbData[i] = {}
end
if tbRes.tbData[i][j] == nil then
tbRes.tbData[i][j] = 0
end
for k = 1, tbSource.nColumn do
tbRes.tbData[i][j] =
tbRes.tbData[i][j] + (tbSource.tbData[i][k] * tbDest.tbData[k][j])
end
end
end
tbRes.nRow = tbSource.nRow
tbRes.nColumn = tbDest.nColumn
return tbRes
end
end
输出结果

LuaToCpp
知识点
luaL_len
这里由于我们接收来源Lua的table数据,luaL_len(两个参数,分别为lua虚拟机状态以及lua堆栈位置)该API由Lua提供,用于获取table表的大小。
lua_newuserdata
该方式主要用于C++端自定义数据,该数据存放至lua端(即所占的空间由lua端分配,C++端无需关系其生命周期,lua_newuserdata创建的用户数据生命周期由lua的gc负责管理)。这里在我们平常使用的时候会遇到一些问题,比如C++的STL库等。由于lua是使用C语言实现的,并没有STL库以及内部模板这些概念,所以如果我们使用下面的语句(下方)当我们的用户数据userdata从lua端回来时,会出现无法解析的情况,从而导致C++程序崩溃。
Matrix* pp = (Matrix*)lua_newuserdata(L, sizeof(Matrix)); //Matrix实体的空间由lua分配,无法解析其中的vector stl容器
那么我们如何解决这个问题呢?利用一下巧妙的方式即可完美解决。
Matrix** pp = (Matrix**)lua_newuserdata(L, sizeof(Matrix*));
*pp = new Matrix(); //该部分内存由C++分配
那就是在lua端我们分配的是Matrix实体地址所占用的空间(一般为4个字节或8个字节),也就是说我们在lua端分配的空间中存储的只是类实体的地址,而真正的类实体实在C++端进行分配的,这样每次我们从lua端回来时我们可以通过在lua端记录的实体地址在C++端索引具体类实体所在地。
LuaToCpp.cpp
#include <iostream>
#include "lua.hpp"
#include "Matrix.hpp"
#define CPP_MATRIX "CPP_MATRIX"
static int gs_Top = 0;
#define STACK_NUM(L) \
gs_Top = lua_gettop(L); \
std::cout<<"stack top:"<< gs_Top <<std::endl\
extern "C" {
static int InitMatrix(lua_State* L) {
//STACK_NUM(L);
//std::cout << "len:" << luaL_len(L, -1) << std::endl;
int32_t row = luaL_len(L, -1);
//STACK_NUM(L);
lua_rawgeti(L, -1, 1);
int32_t col = luaL_len(L, -1);
//STACK_NUM(L);
lua_pop(L, 1);
std::vector<std::vector<double>> inputData;
for (int32_t i = 0; i < row; i++) {
lua_rawgeti(L, -1, i + 1);
std::vector<double> data;
for (int32_t j = 0; j < col; j++) {
lua_rawgeti(L, -1, j + 1);
data.push_back(lua_tonumber(L, -1));
lua_pop(L, 1);
}
inputData.push_back(data);
lua_pop(L, 1);
}
Matrix** pp = (Matrix**)luaL_checkudata(L, 1, CPP_MATRIX);
//STACK_NUM(L);
(*pp)->Init(inputData);
//lua堆栈平衡
//STACK_NUM(L);
lua_pop(L, 2);
//STACK_NUM(L);
return 0;
}
static int UnMatrix(lua_State* L) {
Matrix** pp = (Matrix**)luaL_checkudata(L, 1, CPP_MATRIX);
std::cout << "auto gc" << std::endl;
if (*pp) {
delete *pp;
}
return 0;
}
static int AddMatrix(lua_State* L) {
//STACK_NUM(L);
Matrix** pp1 = (Matrix**)luaL_checkudata(L, 1, CPP_MATRIX);
Matrix** pp2 = (Matrix**)luaL_checkudata(L, 2, CPP_MATRIX);
Matrix** pp = (Matrix**)lua_newuserdata(L, sizeof(Matrix*));
*pp = new Matrix((**pp1) + (**pp2)); //该部分内存由C++分配
luaL_setmetatable(L, CPP_MATRIX);
//STACK_NUM(L);
return 1;
}
static int SubMatrix(lua_State* L) {
//STACK_NUM(L);
Matrix** pp1 = (Matrix**)luaL_checkudata(L, 1, CPP_MATRIX);
Matrix** pp2 = (Matrix**)luaL_checkudata(L, 2, CPP_MATRIX);
Matrix** pp = (Matrix**)lua_newuserdata(L, sizeof(Matrix*));
*pp = new Matrix((**pp1) - (**pp2)); //该部分内存由C++分配
luaL_setmetatable(L, CPP_MATRIX);
//STACK_NUM(L);
return 1;
}
static int MulMatrix(lua_State* L) {
//STACK_NUM(L);
Matrix** pp1 = (Matrix**)luaL_checkudata(L, 1, CPP_MATRIX);
Matrix** pp2 = (Matrix**)luaL_checkudata(L, 2, CPP_MATRIX);
Matrix** pp = (Matrix**)lua_newuserdata(L, sizeof(Matrix*));
*pp = new Matrix((**pp1) * (**pp2)); //该部分内存由C++分配
luaL_setmetatable(L, CPP_MATRIX);
//STACK_NUM(L);
return 1;
}
static int DivMatrix(lua_State* L) {
//STACK_NUM(L);
Matrix** pp1 = (Matrix**)luaL_checkudata(L, 1, CPP_MATRIX);
Matrix** pp2 = (Matrix**)luaL_checkudata(L, 2, CPP_MATRIX);
Matrix** pp = (Matrix**)lua_newuserdata(L, sizeof(Matrix*));
*pp = new Matrix((**pp1) / (**pp2)); //该部分内存由C++分配
luaL_setmetatable(L, CPP_MATRIX);
//STACK_NUM(L);
return 1;
}
static int PrintMatrix(lua_State* L) {
Matrix** pp = (Matrix**)luaL_checkudata(L, 1, CPP_MATRIX);
(*pp)->Print();
return 0;
}
static int CreateMatrix(lua_State* L) {
Matrix** pp = (Matrix**)lua_newuserdata(L, sizeof(Matrix*));
*pp = new Matrix(); //该部分内存由C++分配
luaL_setmetatable(L, CPP_MATRIX);
//STACK_NUM(L);
return 1;
}
}
static const luaL_Reg MatrixFuncs[] = {
{"InitMatrix", InitMatrix },
{"__gc", UnMatrix },
{"__add", AddMatrix },
{"__sub", SubMatrix },
{"__mul", MulMatrix },
{"__div", DivMatrix },
{"PrintMatrix",PrintMatrix },
{NULL, NULL }
};
extern "C" {
static bool CreateMatrixMetaTable(lua_State* L) {
luaL_newmetatable(L, CPP_MATRIX);
lua_pushvalue(L, -1);
lua_setfield(L, -2, "__index");
luaL_setfuncs(L, MatrixFuncs, 0);
//STACK_NUM(L);
lua_pop(L, 1);
return true;
}
}
int main() {
lua_State* L = luaL_newstate();
luaL_openlibs(L);
CreateMatrixMetaTable(L);
//注册构造对象方法
lua_pushcfunction(L, CreateMatrix);
lua_setglobal(L, "CreateMatrix");
if (luaL_dofile(L, "matrix2.0.lua")) {
printf("%s\n", lua_tostring(L, -1));
}
lua_close(L);
return 0;
}
matrix2.0.lua
local _class = {}
function class(super)
local tbClassType = {}
tbClassType.Ctor = false
tbClassType.super = super
tbClassType.New = function(...)
local tbObj = {}
do
local funcCreate
funcCreate = function(tbClass,...)
if tbClass.super then
funcCreate(tbClass.super,...)
end
if tbClass.Ctor then
tbClass.Ctor(tbObj,...)
end
end
funcCreate(tbClassType,...)
end
-- 防止调用Ctor初始化时,在Ctor内部设置了元表的情况发生
if getmetatable(tbObj) then
getmetatable(tbObj).__index = _class[tbClassType]
else
setmetatable(tbObj, { __index = _class[tbClassType] })
end
return tbObj
end
local vtbl = {}
_class[tbClassType] = vtbl
setmetatable(tbClassType, { __newindex =
function(tb,k,v)
vtbl[k] = v
end
})
if super then
setmetatable(vtbl, { __index =
function(tb,k)
local varRet = _class[super][k]
vtbl[k] = varRet
return varRet
end
})
end
return tbClassType
end
Matrix = class()
function Matrix:Ctor(data)
self.tbData = data
self.nRow = #data
if self.nRow > 0 then
self.nColumn = (#data[1])
else
self.nColumn = 0
end
-- print("row:",self.nRow," col:",self.nColumn)
setmetatable(self,{
__add = function(tbSource, tbDest)
assert(tbSource,"tbSource not exist")
assert(tbDest, "tbDest not exist")
local tbRes = Matrix.New({})
-- print(tbSource,tbDest)
-- print("tbSource:",tbSource.nRow,tbSource.nColumn)
-- tbSource:Print()
-- print("tbDest:",tbDest.nRow,tbDest.nColumn)
-- tbDest:Print()
if tbSource.nRow ~= tbDest.nRow
or tbSource.nColumn ~= tbDest.nColumn then
print("row or column not equal...")
return tbRes
else
for rowKey,rowValue in ipairs(tbSource.tbData) do
for colKey,colValue in ipairs(tbSource.tbData[rowKey]) do
if tbRes.tbData[rowKey] == nil then
tbRes.tbData[rowKey] = {}
end
if tbRes.tbData[rowKey][colKey] == nil then
tbRes.tbData[rowKey][colKey] = 0
end
tbRes.tbData[rowKey][colKey] =
tbSource.tbData[rowKey][colKey] + tbDest.tbData[rowKey][colKey]
end
end
tbRes.nRow = tbSource.nRow
tbRes.nColumn = tbSource.nColumn
return tbRes
end
end,
__sub = function(tbSource, tbDest)
assert(tbSource,"tbSource not exist")
assert(tbDest, "tbDest not exist")
local tbRes = Matrix.New({})
if tbSource.nRow ~= tbDest.nRow
or tbSource.nColumn ~= tbDest.nColumn then
print("row or column not equal...")
return tbRes
else
for rowKey,rowValue in ipairs(tbSource.tbData) do
for colKey,colValue in ipairs(tbSource.tbData[rowKey]) do
if tbRes.tbData[rowKey] == nil then
tbRes.tbData[rowKey] = {}
end
if tbRes.tbData[rowKey][colKey] == nil then
tbRes.tbData[rowKey][colKey] = 0
end
tbRes.tbData[rowKey][colKey] =
tbSource.tbData[rowKey][colKey] - tbDest.tbData[rowKey][colKey]
end
end
tbRes.nRow = tbSource.nRow
tbRes.nColumn = tbSource.nColumn
return tbRes
end
end,
__mul = function(tbSource, tbDest)
return self:_MartixMul(tbSource, tbDest)
end,
__div = function(tbSource, tbDest)
assert(tbSource,"tbSource not exist")
assert(tbDest, "tbDest not exist")
local nDet = self:_GetDetValue(tbDest)
if nDet == 0 then
print("matrix no inverse matrix...")
return nil
end
-- print("det ",nDet)
local tbInverseDest = self:_MatrixNumMul(self:_GetCompanyMatrix(tbDest), 1 / nDet)
-- self:_GetCompanyMatrix(tbDest):Print()
-- print(nDet)
tbInverseDest:Print()
return self:_MartixMul(tbSource, tbInverseDest)
end
}
)
end
function Matrix:Print()
for rowKey,rowValue in ipairs(self.tbData) do
for colKey,colValue in ipairs(self.tbData[rowKey]) do
io.write(self.tbData[rowKey][colKey],',')
end
print('')
end
end
-- 加
function Matrix:Add(matrix)
return self + matrix
end
-- 减
function Matrix:Sub(matrix)
return self - matrix
end
-- 乘
function Matrix:Mul(matrix)
return self * matrix
end
-- 除
function Matrix:Div(matrix)
return self / matrix
end
-- 切割,切去第rowIndex以及第colIndex列
function Matrix:_CutoffMatrix(tbMatrix, rowIndex, colIndex)
assert(tbMatrix,"tbMatrix not exist")
assert(rowIndex >= 1,"rowIndex < 1")
assert(colIndex >= 1,"colIndex < 1")
local tbRes = Matrix.New({})
tbRes.nRow = tbMatrix.nRow - 1
tbRes.nColumn = tbMatrix.nColumn - 1
for i = 1, tbMatrix.nRow - 1 do
for j = 1, tbMatrix.nColumn - 1 do
if tbRes.tbData[i] == nil then
tbRes.tbData[i] = {}
end
local nRowDir = 0
local nColDir = 0
if i >= rowIndex then
nRowDir = 1
end
if j >= colIndex then
nColDir = 1
end
tbRes.tbData[i][j] = tbMatrix.tbData[i + nRowDir][j + nColDir]
end
end
return tbRes
end
-- 获取矩阵的行列式对应的值
function Matrix:_GetDetValue(tbMatrix)
assert(tbMatrix,"tbMatrix not exist")
-- 当矩阵为一阶矩阵时,直接返回A中唯一的元素
if tbMatrix.nRow == 1 then
return tbMatrix.tbData[1][1]
end
local nAns = 0
for i = 1, tbMatrix.nColumn do
local nFlag = -1
if i % 2 ~= 0 then
nFlag = 1
end
nAns =
nAns + tbMatrix.tbData[1][i] *
self:_GetDetValue(self:_CutoffMatrix(tbMatrix, 1, i)) * nFlag
-- print("_GetDetValue nflag:",nFlag)
end
return nAns
end
-- 获取矩阵的伴随矩阵
function Matrix:_GetCompanyMatrix(tbMatrix)
assert(tbMatrix,"tbMatrix not exist")
local tbRes = Matrix.New({})
-- 伴随矩阵与原矩阵存在转置关系
tbRes.nRow = tbMatrix.nColumn
tbRes.nColumn = tbMatrix.nRow
for i = 1, tbMatrix.nRow do
for j = 1, tbMatrix.nColumn do
local nFlag = 1
if ((i + j) % 2) ~= 0 then
nFlag = -1
end
if tbRes.tbData[j] == nil then
tbRes.tbData[j] = {}
end
-- print(Matrix:_GetDetValue(Matrix:_CutoffMatrix(tbMatrix, i, j)))
-- Matrix:_CutoffMatrix(tbMatrix, i, j):Print()
-- print("---11----")
tbRes.tbData[j][i] =
self:_GetDetValue(self:_CutoffMatrix(tbMatrix, i, j)) * nFlag
end
end
return tbRes
end
-- 矩阵数乘
function Matrix:_MatrixNumMul(tbMatrix, num)
for i = 1, tbMatrix.nRow do
for j = 1, tbMatrix.nColumn do
tbMatrix.tbData[i][j] = tbMatrix.tbData[i][j] * num
end
end
return tbMatrix
end
-- 矩阵相乘
function Matrix:_MartixMul(tbSource, tbDest)
assert(tbSource,"tbSource not exist")
assert(tbDest, "tbDest not exist")
if tbSource.nColumn ~= tbDest.nRow then
print("column not equal row...")
return tbSource
else
local tbRes = Matrix.New({})
for i = 1, tbSource.nRow do
for j = 1, tbDest.nColumn do
if tbRes.tbData[i] == nil then
tbRes.tbData[i] = {}
end
if tbRes.tbData[i][j] == nil then
tbRes.tbData[i][j] = 0
end
for k = 1, tbSource.nColumn do
tbRes.tbData[i][j] =
tbRes.tbData[i][j] + (tbSource.tbData[i][k] * tbDest.tbData[k][j])
end
end
end
tbRes.nRow = tbSource.nRow
tbRes.nColumn = tbDest.nColumn
return tbRes
end
end
-- 矩阵加法
local matrix1 = Matrix.New({{1,2,3},{4,5,6}})
local matrix2 = Matrix.New({{2,3,4},{5,6,7}})
-- local matrix3 = matrix1 + matrix2
local matrix3 = matrix1.Add(matrix1,matrix2)
matrix3:Print()
print("-----------------------------------")
-- 矩阵减法
local matrix4 = Matrix.New({{1,1,1},{1,1,1}})
local matrix5 = matrix3 - matrix4
matrix5:Print()
print("-----------------------------------")
-- 矩阵乘法
local matrix6 = Matrix.New({{1,2,3},{4,5,6}})
local matrix7 = Matrix.New({{7,8},{9,10},{11,12}})
local matrix8 = matrix6 * matrix7
matrix8:Print()
print("-----------------------------------")
-- 矩阵除法
local matrix9 = Matrix.New({{1,2,3},{4,5,6},{7,8,0}})
local matrix10 = Matrix.New({{1,2,1},{1,1,2},{2,1,1}})
local matrix11 = matrix7 / matrix8
matrix11:Print()
-- 加法
local cppMatrix1 = CreateMatrix()
cppMatrix1:InitMatrix({{1,2,3},{4,5,6}})
local cppMatrix2 = CreateMatrix()
cppMatrix2:InitMatrix({{2,3,4},{5,6,7}})
print('-------------------加法----------------------')
local cppMatrix3 = cppMatrix1 + cppMatrix2
cppMatrix3:PrintMatrix()
local matrix1 = Matrix.New({{1,2,3},{4,5,6}})
local matrix2 = Matrix.New({{2,3,4},{5,6,7}})
local matrix3 = matrix1 + matrix2
-- local matrix3 = matrix1.Add(matrix1,matrix2)
matrix3:Print()
-- 减法
local cppMatrix4 = CreateMatrix()
cppMatrix4:InitMatrix({{1,1,1},{1,1,1}})
print('-------------------减法----------------------')
local cppMatrix5 = cppMatrix3 - cppMatrix4
cppMatrix5:PrintMatrix()
local matrix4 = Matrix.New({{1,1,1},{1,1,1}})
local matrix5 = matrix3 - matrix4
matrix5:Print()
-- 乘法
local cppMatrix6 = CreateMatrix()
cppMatrix6:InitMatrix({{1,2,3},{4,5,6}})
local cppMatrix7 = CreateMatrix()
cppMatrix7:InitMatrix({{7,8},{9,10},{11,12}})
print('-------------------乘法----------------------')
local cppMatrix8 = cppMatrix6 * cppMatrix7
cppMatrix8:PrintMatrix()
local matrix6 = Matrix.New({{1,2,3},{4,5,6}})
local matrix7 = Matrix.New({{7,8},{9,10},{11,12}})
local matrix8 = matrix6 * matrix7
matrix8:Print()
-- 除法
local cppMatrix9 = CreateMatrix()
cppMatrix9:InitMatrix({{1,2,3},{4,5,6},{7,8,0}})
local cppMatrix10 = CreateMatrix()
cppMatrix10:InitMatrix({{1,2,1},{1,1,2},{2,1,1}})
print('-------------------除法----------------------')
local cppMatrix11 = cppMatrix9 / cppMatrix10
cppMatrix11:PrintMatrix()
local matrix9 = Matrix.New({{1,2,3},{4,5,6},{7,8,0}})
local matrix10 = Matrix.New({{1,2,1},{1,1,2},{2,1,1}})
local matrix11 = matrix9 / matrix10
matrix11:Print()
输出结果

![[Java 进阶] synchronized 与 ReentrantLock的区别](https://img-blog.csdnimg.cn/6fff8d64b4a04f89935dcc4bf57350d0.png)