电子技术——共源共栅放大器

之前我们提到过，提高基础增益单元（共源放大器）的一种方法是提高其 $r_o$ 的阻值，之后我们学过共栅放大器作为电流缓冲器可以做到这一点，自然地我们就得到了终极解决方案，也就是共源共栅放大器。

共源共栅结构

共源共栅结构指的是共源放大器作为主要增益单元，共栅放大器作为电流缓冲器，下图展示了这种结构：

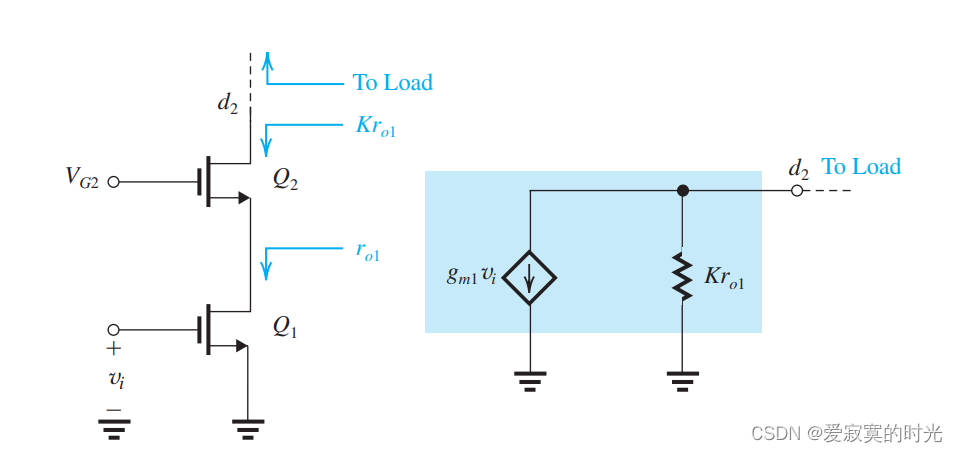
这里 $Q_1$ 是放大器（省略了DC偏置）， $Q_2$ 作为电流缓冲器，偏置在 $V_{G2}$ （信号地）上。之后我们会介绍同样的BJT版本的结构。

之前我们知道，电流缓冲器的电流不变，将输出阻抗提升了 $K$ 倍，因此共源共栅结构的一种抽象表示如右图。

MOS共源共栅结构

下图展示了一个理想的MOS共源共栅结构，使用一个理想电流源作为偏置：

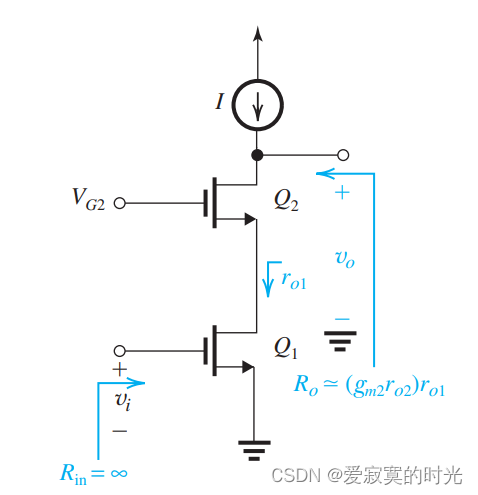
其等效的抽象模型为：

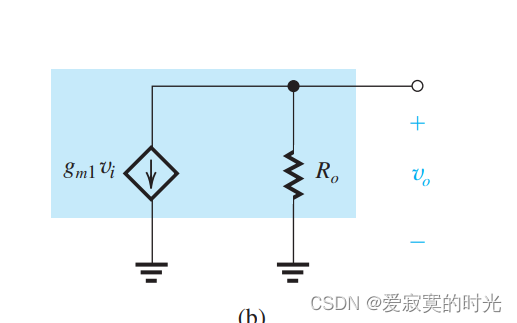
因为电流源是理想的，也就是说阻抗为无穷大，此时的开路增益为：

$$A_{vo}=-g_{m1}{R}_o$$

又因为 $Q_1$ 的输出阻抗是 $r_{o1}$ ， $Q_2$ 将输出阻抗提升约 $g_{m2}{r}_{o2}$ 倍，因此：

$$R_o\simeq (g_{m2}{r}_{o2})r_{o1}$$

带入得到：

$$A_{vo}=-(g_{m1}{r}_{o1})(g_{m2}{r}_{o2})$$

假设 $Q_1$ 和 $Q_2$ 完全匹配，也就是 $g_{m1}=g_{m2}=g_m$ 和 $r_{o1}=r_{o2}=r_o$ ，则得到：

$$A_{vo}=-(g_m{r}_o{)}^2=-A_0^2$$

所以MOS共源共栅结构将之前的固有增益从原来的 $A_0$ 近似提升至 $A_0^2$ 。

接下来考虑电流源不完美的情况，假设电流源是使用的PMOS电流镜，如下图：

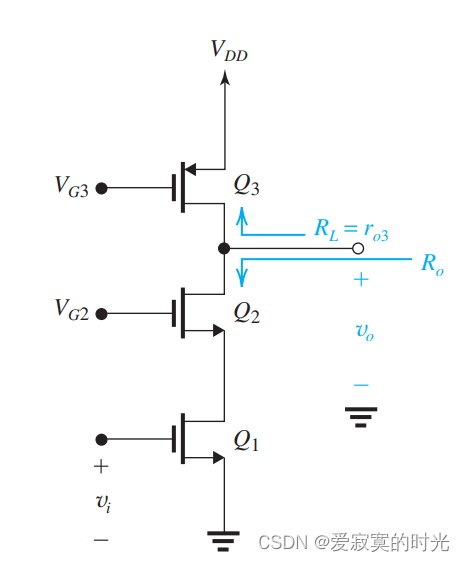
则此时负载电阻阻值为 $R_L=r_{o3}$ 。此时的电压增益是：

$$A_v=-g_{m1}(R_o||R_L)=-g_{m1}(g_{m2}{r}_{o2}{r}_{o1}||r_{o3})$$

注意到 $R_L\ll R_o$ ，因此：

$$A_v\simeq -g_{m1}{r}_{o3}$$

此时的电压增益又退回到 $A_0$ ，这里电流缓冲器 $Q_2$ 的作用失效了。也就是说，只是提升 $Q_1$ 的输出阻抗是没用的，我们还必须要提升 $Q_3$ 的输出阻抗。

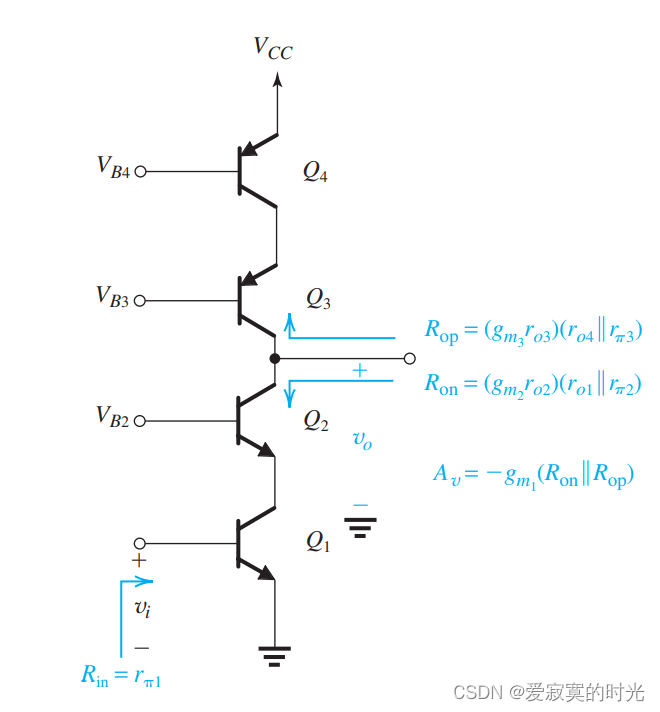
自然地可以想到，可以在 $Q_3$ 同样串联一个电流缓冲器，如图：

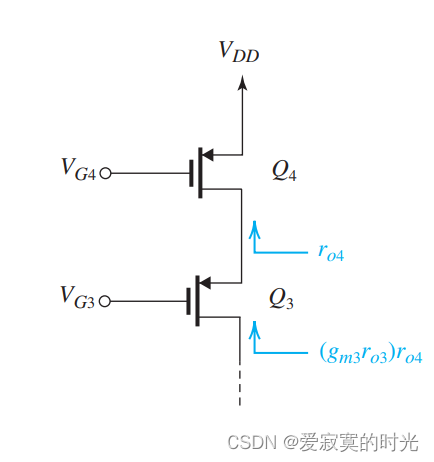
此时整个电路结构变为：

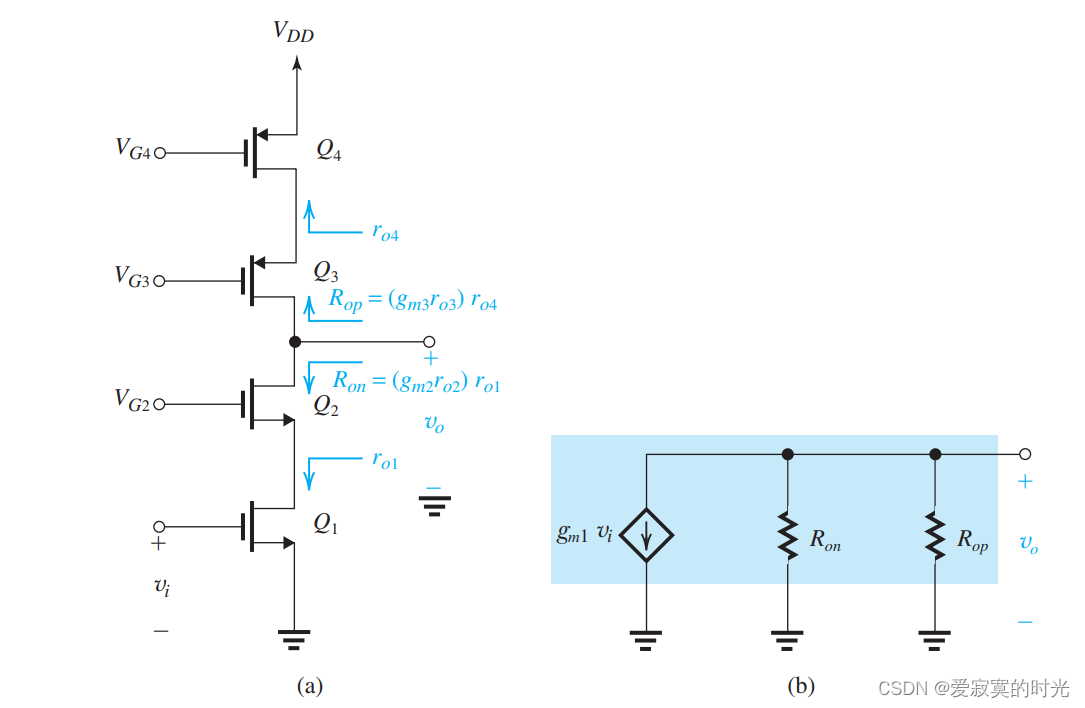
则此时电流源的输出电阻变为：

$$R_o=(g_{m3}{r}_{o3})r_{o4}$$

整个电路等效于右边的抽象模型，因此电压增益变为：

$$A_v=-g_{m1}[R_{on}||R_{op}]=-g_{m1}[[(g_{m2}{r}_{o2})r_{o1}]||[(g_{m3}{r}_{o3})r_{o4}]]$$

假设四个晶体管完全匹配，得到：

$$A_v=-\frac{1}{2}{A}_0^2$$

此时的电压增益与 $A_0^2$ 同阶，是我们想要的结果。

共源共栅放大器中的电压增益分配

现在我们探究共源共栅放大器的整体增益是怎样在共源共栅放大器中的电压增益分配的。在这里，不失一般性的我们将负载阻抗表示为 $R_L$ 如下图：

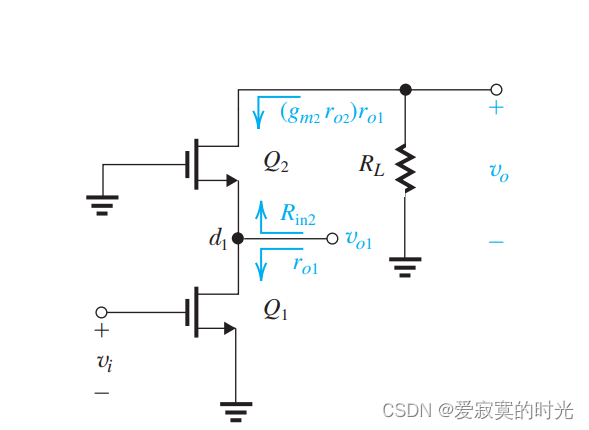
则此时的电压增益为：

$$A_v=-g_{m1}(R_o||R_L)=-g_{m1}(g_{m2}{r}_{o2}{r}_{o1}||R_L)$$

上图中的电压增益还可以表示为两级增益：

$$A_v=A_{v1}{A}_{v2}=(\frac{v_{o1}}{v_i})(\frac{v_o}{v_{o1}})$$

为了计算 $A_{v1}$ ，我们将从 $Q_1$ 的漏极到地直接的阻抗记为 $R_{d1}$ ，如图：

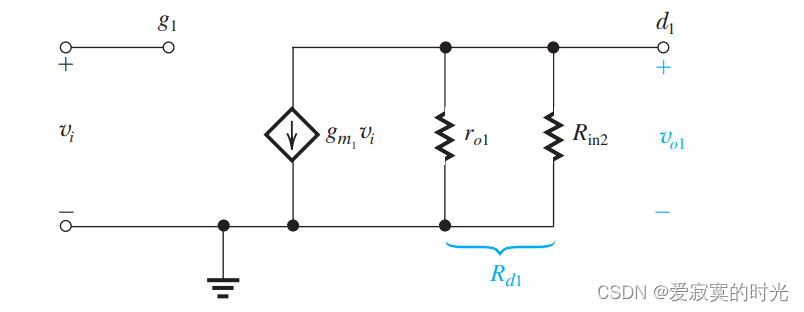
则：

$$A_{v1}=-g_{m1}{R}_{d1}$$

这里 $R_{d1}=r_{o1}||R_{in2}$ ， $R_{in2}$ 是CG级的输入阻抗：

$$R_{in2}=\frac{R_L}{g_{m2}{r}_{o2}}+\frac{1}{g_{m2}}$$

那么 $A_{v2}=A_v/A_{v1}$ 。基于上述方法，根据 $R_L$ 的不同，我们可以得到下图表的两级增益分配情况：

四种情况分别为（假设MOS管完全匹配）：

1. $R_L=\infty$ 表示负载是理想电流源。
2. $R_L=(g_m{r}_o)r_o$ 表示负载是共源共栅电流源。
3. $R_L=r_o$ 表示负载是简单电流镜。
4. $R_L=0$ 理论最坏情况，此时负载短路。

其中情况一代表了共源共栅结构的理论最大增益，情况二代表了一般情况。但是情况三并不是无用，在以后我们会学到，情况三具有优秀的高频响应。

共源双级共栅放大器

如果还需要更高的电压增益，那么就需要更高的输出阻抗，自然想到我们可以在加一级共栅结构，构成两级电流缓冲器，如图：

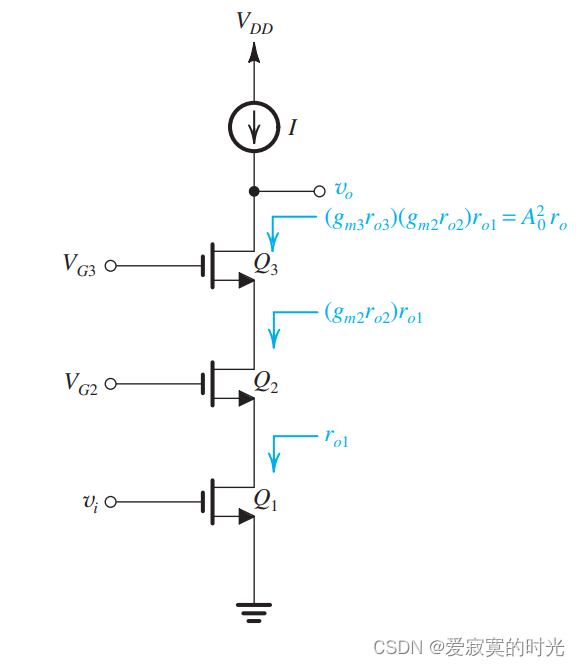
此时通过计算可以算出，电压增益为：

$$A_v=A_0^3$$

这种结构的一个缺点就是，会造成晶体管在同一条漏极支路上堆叠：只提高CS放大器的输出阻抗是不够的，还要提高电流镜的输出阻抗，因此电流镜的输出端也需要再加一级的共栅结构，此时整个漏极支路上总共有6个MOS晶体管，因为每个晶体管都需要工作在饱和区下，每个晶体管的 $v_{DS}$ 最小不能小于 $V_{OV}$ 。因此总压降在 $6v_{DS}$ ，那么就必须提高 $V_{DD}$ 的值。但是我们知道，对于IC来说 $V_{DD}$ 一般在1V到2V左右，这就限制了漏极支路中的最大MOS晶体管数量。

折叠共源共栅放大器

为了避免晶体管在同一条漏极支路上堆叠，我们的CG结构可以通过PMOS实现，如下图：

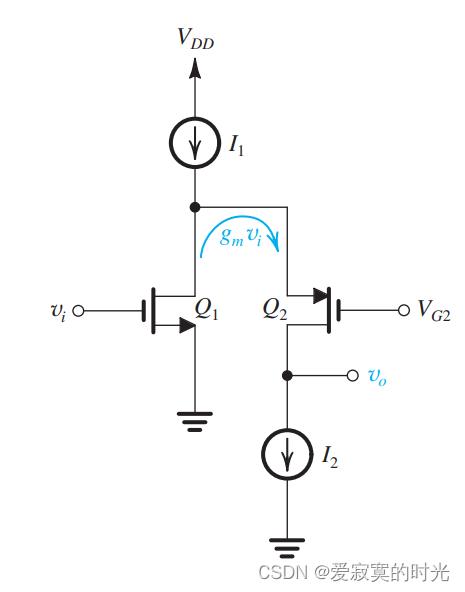
现在 $Q_1$ 偏置在 $I_1-I_2$ 上， $Q_2$ 是我们的PMOS的CG结构偏置在 $I_2$ 上，电流源 $I_2$ 作为主动负载。

其小信号模型和我们之前普通的共源共栅放大器一样，只不过我们的信号电流 $g_m{v}_i$ 通过PMOS转向折叠流入 $Q_2$ 。因此这个结构称为 折叠共源共栅放大器 。这种折叠结构在IC设计中非常受欢迎。

BJT 共射共基结构

下图展示了具有理想电流源负载的BJT 共射共基结构：

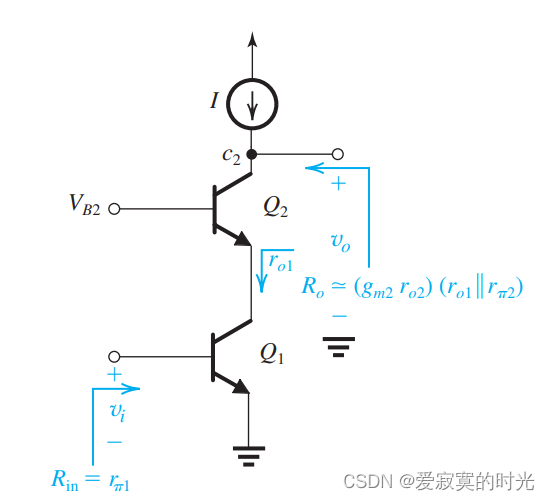
对于该电路的分析和MOS的大体相似，首先因为基极电流，输入阻抗为：

$$R_{in}=r_{\pi 1}$$

假设 $\alpha =1$ ，此时的抽象结构为：

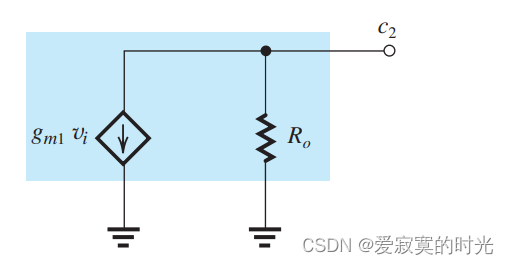
这里：

$$R_o=r_{o2}+(g_{m2}{r}_{o2})(r_{o1}||r_{\pi 2})\simeq (g_{m2}{r}_{o2})(r_{o1}||r_{\pi 2})$$

别看这个结果和MOS的相似，但这个结果只是一个近似的结果，因为基极的有限电流。就是因为有限的 $\beta$ 存在，导致了括号中的并联计算，这导致BJT电流缓冲器存在理论最大值：

$$R_o{|}_{max}={\beta }_2{r}_{o2}$$

因为存在理论最大值，也就是说无论怎么提高CB的信号源阻抗，CB的输出阻抗总是无法突破理论最大值。所以不像MOS，使用多级BJT电流缓冲器是没有意义的。

开路增益为：

$$A_{vo}=-g_{m1}(g_{m2}{r}_{o2})(r_{o1}||r_{\pi 2})$$

对于完美匹配：

$$A_{vo}=-(g_m{r}_o)[g_m(r_o||r_{\pi })]$$

小于 $(g_m{r}_o{)}^2$ 。当 $r_o=\infty$ 的时候存在理论最大值：

$$|A_{vo}{|}_{max}=\beta g_m{r}_o=\beta A_0$$

下图展示了BJT的共射双级共基结构：