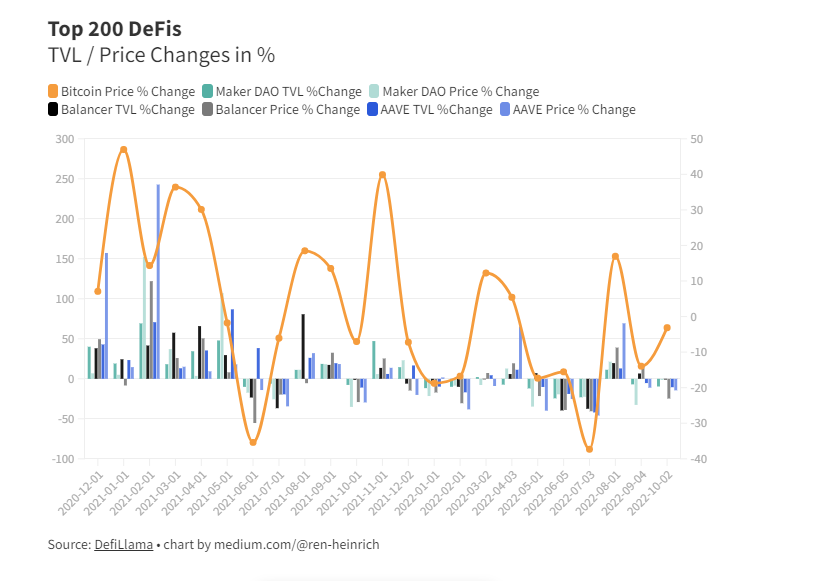
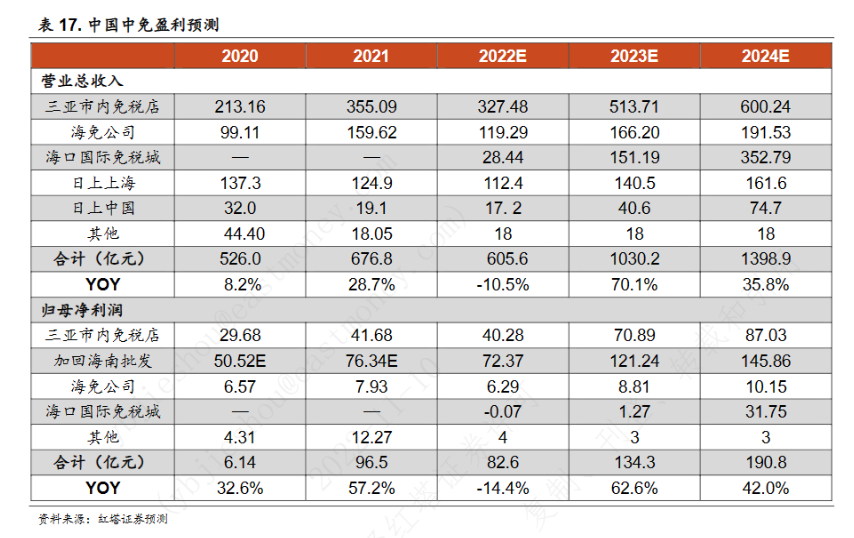
第五十一章 BFS进阶(一)——双端队列广搜
- 一、原理
- 二、例题
- 1、问题
- 2、分析
- 三、代码
一、原理
在介绍双端队列广搜之前,我们先回顾一下堆优化版本的 d i j k s t r a dijkstra dijkstra算法。
在这个算法中,我们使用的是小根堆来找到距离起点的最小值。而这个最小值就是该点到起点的最短距离。然后我们再用这个最小值去松弛该点的临边。
如果临边松弛成功,就让这个点进入我们的优先队列。
今天所涉及到的双端队列广搜相当于一个特殊情况下的dijkstra算法。
我们先来剖析一下之前的朴素版本的BFS。
我们的朴素版本的BFS也用到了一个队列,只不过我们用的是普通队列。
那么这个队列有什么特殊的性质呢?
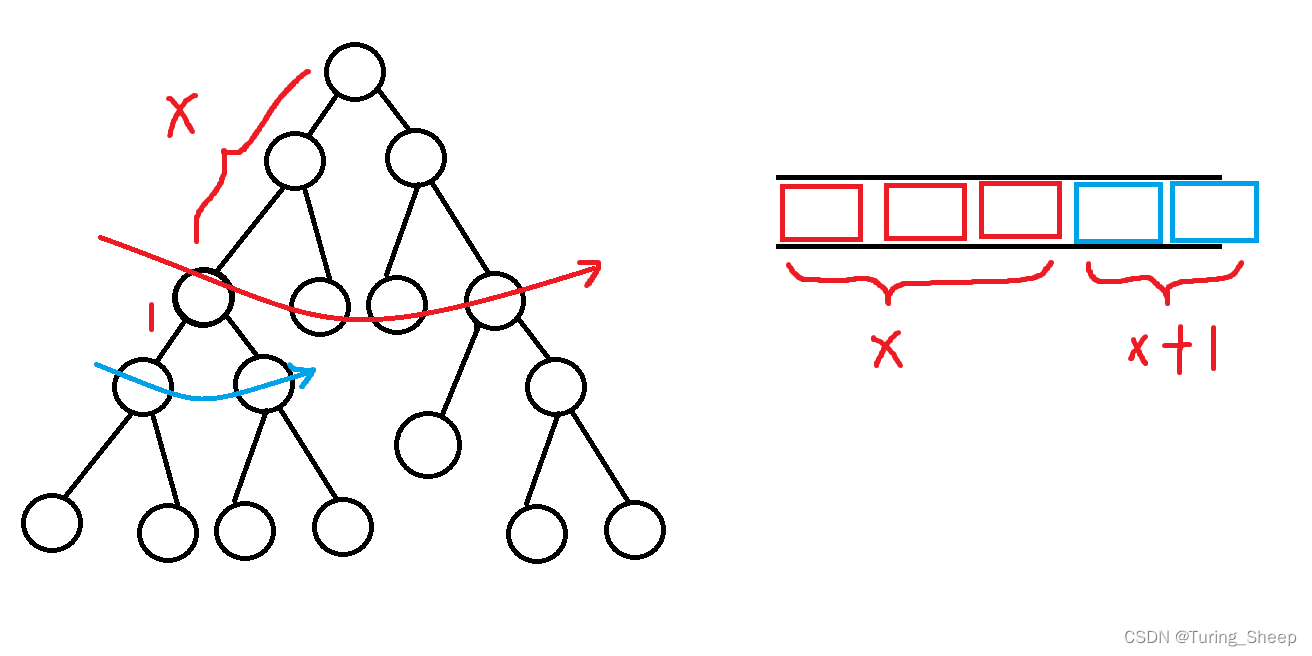
我们假设现在BFS到了红色线所在的层,那么假设第一个红色点出队,然后该红色点又更新了两个蓝色点,那么这两个点也会进队列。
那么我们就发现队列中的点是符合二段性的。
即前一段到原点的距离是x,后一段到原点的距离是x+1,不可能出现第三段。
因为如果出现了第三段,一定是从第二段的x+1扩展出来的。而轮到第二段出队的时候,第一段肯定早就出队了,此时队列中是第二段和第三段,依旧符合二段性。
那么这个二段性还有一个特殊的地方,它是距离小的一段在前面,距离大的一段在后面,这就符合了单调递增的性质。
因此,我们的队头就是最小的,也就是说在这种特殊的情况下, 我们的队列达到了和优先队列一样的效果。
那么知道了这个有什么用呢?
我们可以换一个角度,我们把第一段的x看作x+0。
此时,我们我们的图就不在是只存在边权为1的图,而是存在边权为1和0的图。
有了这个思路以后,我们再来模拟一下dijkstra的过程。
当队头出队的时候,此时是距离原点最近的点。假设这个最小距离是x,该点是A。
再给A设置几个邻接点:B,C,D。
这三个点到A的距离是0,1,0。
不妨让A点成功松弛这几个点,那么这几个点都会入队。
其中B到原点的距离就是x+0,C到原点的距离就是x+1,D到原点的距离就是x + 0
那么为了维护我们队列的二段性,我们就会把B和D点放到队列中的前半段,C放到队列中的后半段。
即从两边插入队列。
好,现在我们就发现,当一个图中存在只存在两个非负边权的时候,我们就能够通过维护一个队列的二段性,来实现一个简易地dijkstra算法。
于是我们就把这种方式叫做双端队列广搜。
二、例题
1、问题

2、分析
这个我们就可以把翻转电线的次数看作边权,如果不翻转的话,就是0,如果翻转的话就是1。
现在让求的是最小的翻转次数,即从(0,0)右下角的最短路径。
由于只存在两个非负边权,因此我们可以使用双端队列广搜算法。
这道题在知道该算法后,还有一个难点就是如何建图。
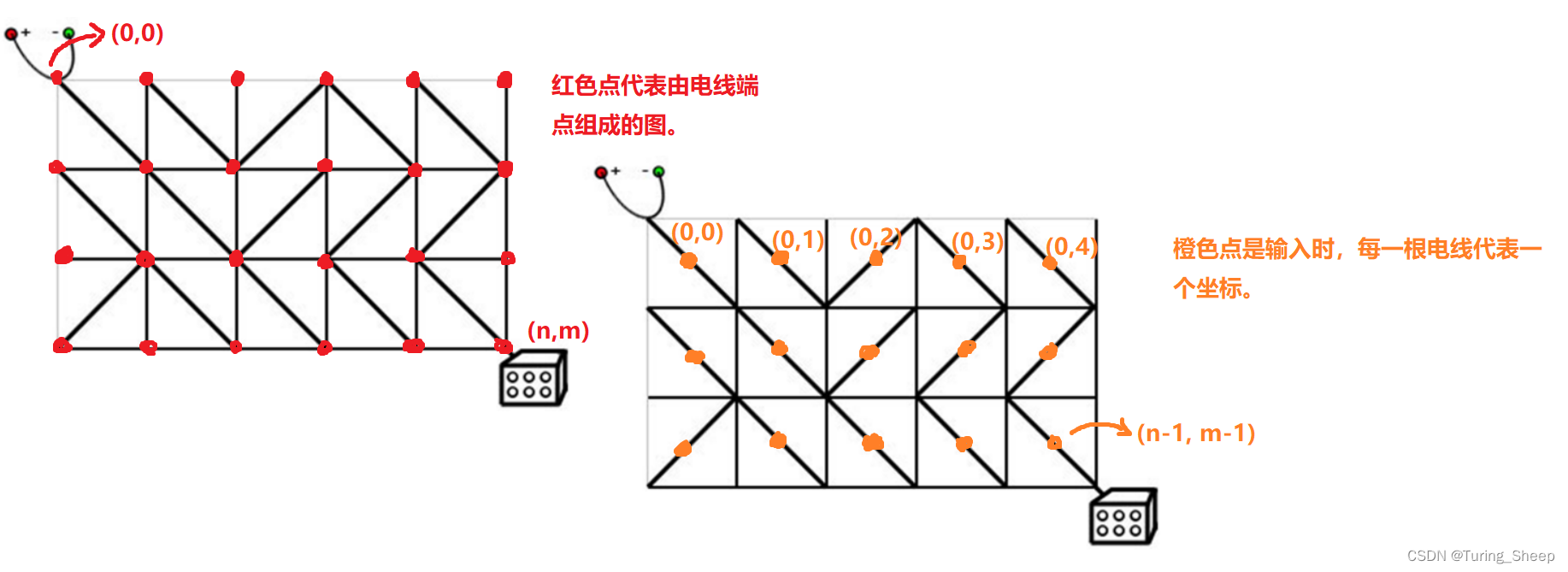
我们的BFS是在红色图中进行的,因此我们先看看红色图中的某个点可以向哪几个方向BFS。
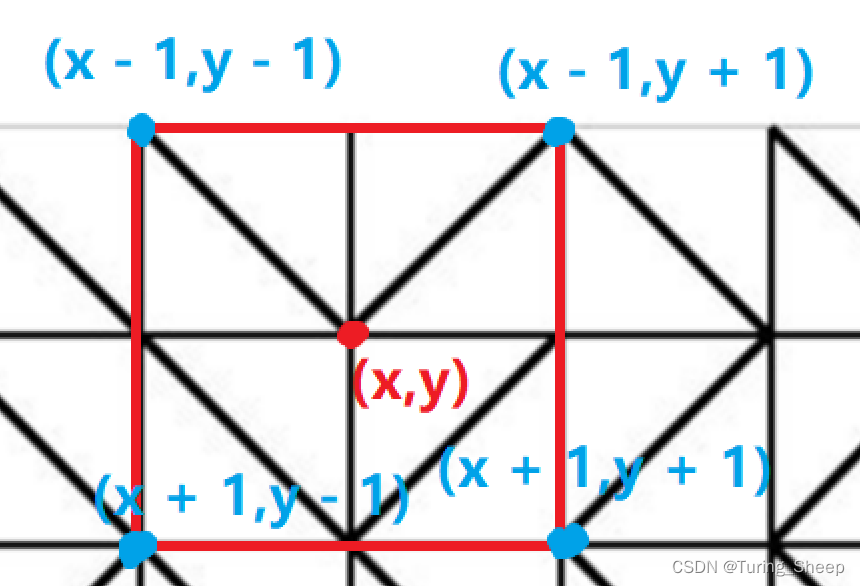
除了记录它能向哪个方向拓展外,我们还需要记录一下,它是沿着怎样放置的一根电线到达的。
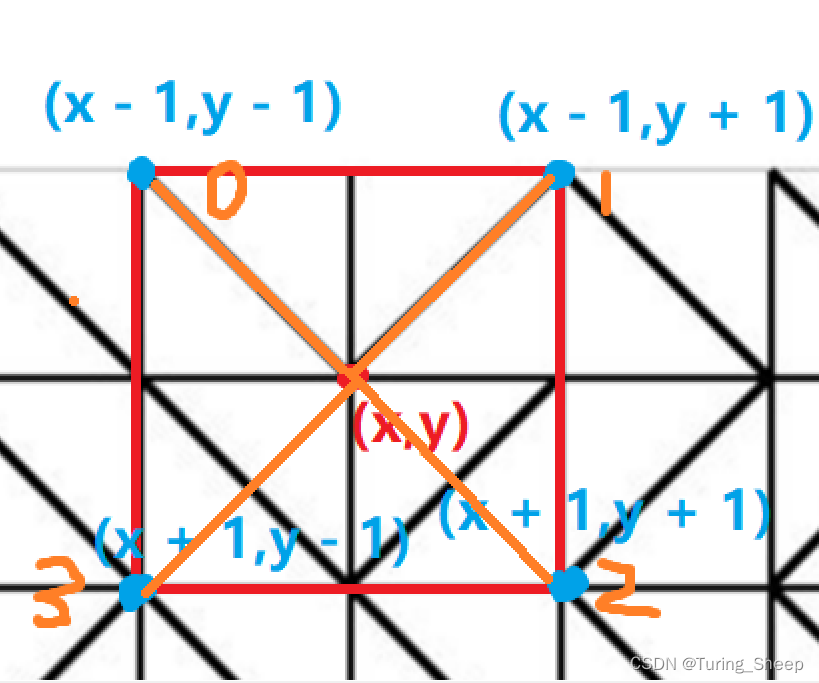
给图中的四个点标号。
图中的橙色线就是我们通过中心点,到达标号点所需要经过的电线。
我们如果按照标号存下来的话,字符串就是“\ / \ /”
但是“\”是特殊字符,我们需要再输入一个反斜杠即,“\\ / \\ /”
那么这个橙色线是理论上,电线的放置形状。
我们还需要通过中心点,找到该点实际上的电线放置情况。
如果二者相同,则说明不用翻转,边权是0,反之是1。
现在要解决的问题,就是如何通过中心点找到对应位置的实际电线放置情况。
我们刚才的橙色坐标图上,是将电线的坐标写在了电线的重心处。
现在我们将电线的坐标移动到电线所在格子的左上角。
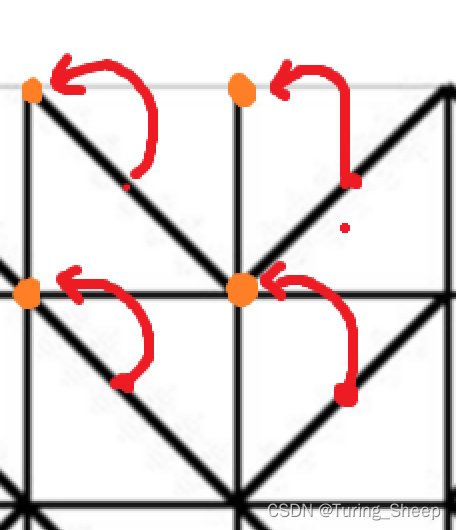
这样这个图就和我们的红色坐标图统一了。
接着我们就可以计算一下,如何通过中心点,通过偏移,找到真实电线的位置。
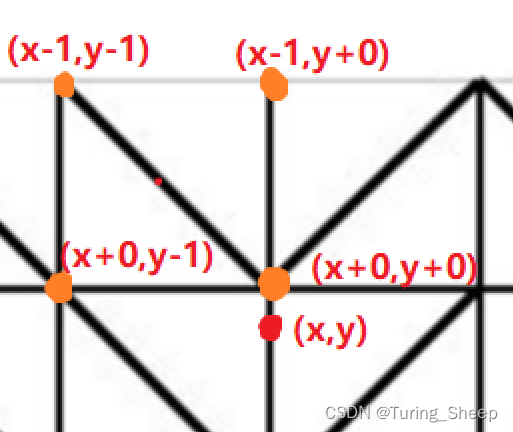
知道了这些后,我们就可以写代码了。
三、代码
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int > pii;
const int N = 510, M = N * N;
const int INF = 0x3f3f3f3f;
int n, m;
char g[N][N];
bool st[N][N];
int dis[N][N];
int bfs()
{
memset(dis, 0x3f, sizeof dis);
memset(st, 0, sizeof st);
deque<pii>q;
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1};
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1};
char cs[] = "\\/\\/";
q.push_front({0, 0});
dis[0][0] = 0;
while(q.size())
{
pii t = q.front();
q.pop_front();
if(st[t.x][t.y])continue;
st[t.x][t.y] = true;
for(int i = 0; i < 4; i ++ )
{
int nx = t.x + dx[i];
int ny = t.y + dy[i];
if(nx >= 0 && nx <= n && ny >= 0 && ny <= m)
{
int d = dis[t.x][t.y] + (g[t.x + ix[i]][t.y + iy[i]] != cs[i]);
if(d < dis[nx][ny])
{
dis[nx][ny] = d;
if(g[t.x + ix[i]][t.y + iy[i]] != cs[i])
{
q.push_back({nx, ny});
}
else
{
q.push_front({nx, ny});
}
}
}
}
}
return dis[n][m];
}
void solve()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
cin >> g[i];
int t = bfs();
if(t == INF)
cout << "NO SOLUTION\n";
else cout << t << "\n";
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t -- )
{
solve();
}
return 0;
}