java基础—Volatile关键字详解

文章目录

java基础—Volatile关键字详解
- - 并发编程的三大特性：
  - volatile的作用是什么
  - volatile如何保证有可见性
  - - volatile保证可见性在JMM层面原理
    - volatile保证可见性在CPU层面原理
    - 可见性问题的例子
  - volatile如何保证有序性
  - - 单例模式使用volatile保证有序性的例子
  - volatile为什么不能保证原子性

并发编程的三大特性：

原子性、可见性和有序性。只要有一条原则没有被保证，就有可能会导致程序运行不正确。volatile关键字被用来保证可见性，即保证共享变量的内存可见性以解决缓存一致性问题。一旦一个共享变量被 volatile关键字修饰，那么就具备了两层语义：内存可见性和禁止进行指令重排序。

原子性：就是一个操作或多个操作中，要么全部执行，要么全部不执行。

例如：账户A向账户B转账1000元，这个么过程涉及到两个操作，(1)A账户减去1000元 (2)B账户增加1000元。这么两个操作必须具备原子性。否则A账户钱少了，B账户没增加。
有序性： 程序执行顺序按照代码先后顺序执行。

处理器为了提高程序运行效率，可能会对输入代码进行优化，它不保证程序中各个语句的执行先后顺序同代码中的顺序一致(指令重排)，但是它会保证程序最终执行结果和代码顺序执行的结果是一致的。(此处的结果一致指的是在单线程情况下)

指令重排的理解：单线程侠，如果两个操作更换位置后，对后续操作结果没有影响，可以对这两个操作可以互换顺序。
可见性： 可见性是指多线程共享一个变量，其中一个线程改变了变量值，其他线程能够立即看到修改的值。
```
//线程1执行的代码
int i = 0;
i = 10;
//线程2执行的代码
j = i;
```
CPU1执行线程1代码，CPU执行线程2代码。CPU读取i=0到CPU缓存中，修改i=10到自己缓存，还没更新到主存，此时CPU2读取的i还是主存中i=0,此时j会被赋值为0；

volatile的作用是什么

volatile是一个类型修饰符，JDK1.5之后，对其语义进行了增强。

保证了不同线程之间对共享变量操作的可见性。
通过禁止编译器、CPU指令重排序和部分hapens-before规则，解决有序性。

volatile如何保证有可见性

volatile保证可见性在JMM层面原理

volatile修饰的共享变量在执行写操作后，会立即刷回到主存，以供其它线程读取到最新的记录。

volatile保证可见性在CPU层面原理

volatile关键字底层通过lock前缀指令，进行缓存一致性的缓存锁定方案，通过总线嗅探和MESI协议来保证多核缓存的一致性问题，保证多个线程读取到最新内容。 lock前缀指令除了具有缓存锁定这样的原子操作，它还具有类似内存屏障的功能，能够保证指令重排的问题。

被volatile修饰的变量在写操作生成汇编指令时，会多出Lock前缀指令，这个指令会引起CPU缓存刷回主存。
刷回主存后，导致其他核心缓存了该内存地址的数据无效，通过缓存一致性协议(MESI)保证每个线程的数据是最新的。
缓存一致性协议保证每个CPU核心通过嗅探在总线上传播的数据来检查自己的缓存是不是被修改，· 当 CPU 发现自己缓存行对应的内存地址被修改，会将当前 CPU 的缓存行设置成无效状态，重新从内存中把数据读到 CPU 缓存

可见性问题的例子

启动线程1和线程2，线程2设置stop=true。查看线程1是否会停止

public class TestVisibility {

    //是否停止 变量
    private static boolean stop = false;
    public static void main(String[] args) throws InterruptedException {


        new Thread(() -> {
            System.out.println("线程 1 正在运行...");
            while (!stop) ;
            System.out.println("线程 1 终止");
        }).start();

        //休眠 10 毫秒
        Thread.sleep(10);
        //启动线程 2， 设置 stop = true
        new Thread(() -> {
            System.out.println("线程 2 正在运行...");
            stop = true;
            System.out.println("设置 stop 变量为 true.");
        }).start();
    }
    
}

可见，线程1并不会停止，而是一直循环下去。这就是CPU缓存导致的一致性问题。

给stop加上volatile关键字，并运行，会发现线程1终止了

volatile如何保证有序性

内存屏障(Memory Barrier 又称内存栅栏，是一个 CPU 指令)禁止重排序

Volatile关键字(JMM内存屏障)，内存屏障也成为内存栏杆，是一个CPU指令，volatile修饰的变量，在读写操作前后都会进行屏障的插入来保证执行的顺序不被编译器等优化器锁重排序。

内存屏障的功能有两个：（1）阻止屏障两边的指令重排、（2）刷新处理器缓存（保证内存可见性）
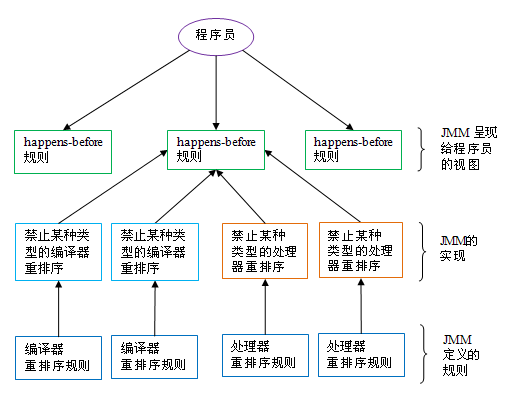
3 个 happens-before 规则实现：
Happens-Before
SR-133 提出了 happens-before 的概念，通过这个概念来阐述操作之间的内存可见性。如果一个操作执行的结果需要对另一个操作可见，那么这两个操作之间必须存在 happens-before 关系。这里提到的两个操作既可以是在一个线程之内，也可以是在不同线程之间。与程序员密切相关的 happens-before 规则如下：
- 程序顺序规则：一个线程中的每个操作，happens- before 于该线程中的任意后续操作。
- 监视器锁规则：对一个监视器锁的解锁，happens- before 于随后对这个监视器锁的加锁。
- volatile 变量规则：对一个 volatile 域的写，happens- before 于任意后续对这个 volatile 域的读。
- 传递性：如果 A happens- before B，且 B happens- before C，那么 A happens- before C。
注意，两个操作之间具有 happens-before 关系，并不意味着前一个操作必须要在后一个操作之前执行！happens-before 仅仅要求前一个操作（执行的结果）对后一个操作可见，且前一个操作按顺序排在第二个操作之前（the first is visible to and ordered before the second）。happens- before 的定义很微妙

单例模式使用volatile保证有序性的例子

为什么变量singleton之前需要加volatile

public class Singleton {
    public static volatile Singleton singleton;

    /**
     * 构造函数私有，禁止外部实例化
     */
    private Singleton() {};

    public static Singleton getInstance() {
        if (singleton == null) {
            synchronized (singleton) {
                if (singleton == null) {
                    singleton = new Singleton();
                }
            }
        }
        return singleton;
    }
}

先要了解对象的构造过程，实例化一个对象其实可以分为三个步骤：

分配内存空间。
初始化对象。
将内存空间的地址赋值给对应的引用。

但是由于操作系统可以对指令进行重排序，所以上面的过程也可能会变成如下过程：

分配内存空间。
将内存空间的地址赋值给对应的引用。
初始化对象

如果是这个流程，多线程环境下就可能将一个未初始化的对象引用暴露出来，从而导致不可预料的结果。因此，为了防止这个过程的重排序，我们需要将变量设置为volatile类型的变量

volatile为什么不能保证原子性

执行下面代码会发现，输出的并不是10000

public class atomiciVolitile {

    volatile  int  i = 0;
    public void addI(){
        i++;
    }

    public static void main(String[] args) throws InterruptedException {
        atomiciVolitile a=new atomiciVolitile();
        for (int i = 0; i < 10000; i++) {
            new Thread(() -> {
                try {
                    Thread.sleep(10);//执行速度太快，没有起到并发作用，等待10毫秒
                } catch (InterruptedException e) {
                    e.printStackTrace();
                }
                a.addI();
            }).start();
        }

        Thread.sleep(5000);

        System.out.println(a.i);

    }
}