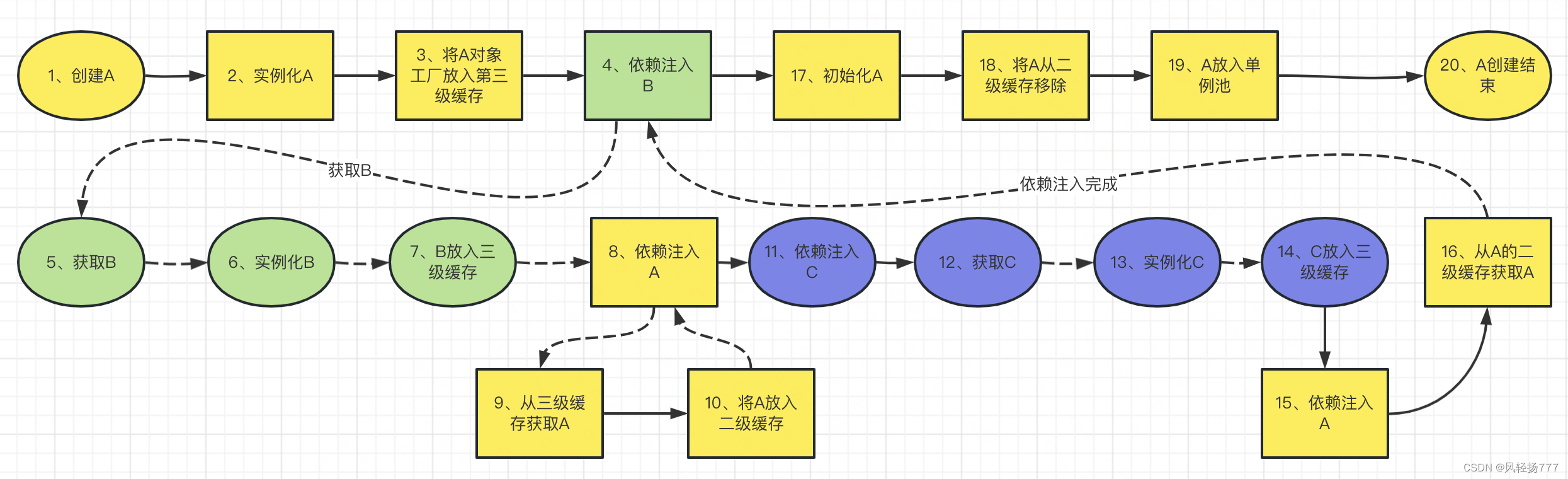
均值假设检验定义

2类错误
- 第1类错误(弃真):当原假设H0为真,观察值却落入拒绝域,因而拒
绝H0这类错误是“以真为假” 犯第一类错误的概率=显著性水平α - 第2类错误(取伪):当原假设H0不真,而观察值却落入接受域,因而
接受H0以假为真
常用形式
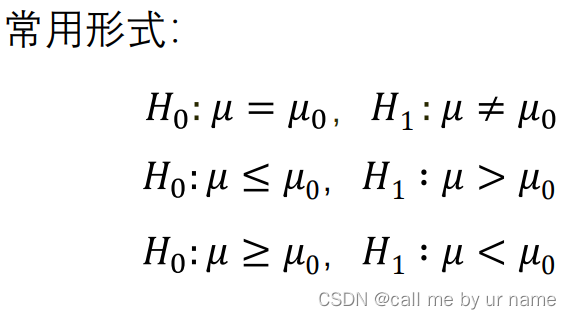
若H0为真,则样本值落入拒绝域{Z>zα/2}的概率是α
若样本值落入拒绝域 就拒绝原假设H0
不拒绝H0,并不意味着H0一定对,只是差异还不够显著,不足以否定H0
但其实,光看上面的这些,还是不太懂知识点的用法
例

未落入拒绝域,所以不能拒绝
如果 t 的绝对值 > 分位点,那么就是落入了拒绝域,会被拒绝
拒绝域的意思就是,满足写出的这个拒绝域公式,就说明落入拒绝域
步骤

正态分布均值的假设检验
单个总体
σ2已知 – z检验

注意:μ≤μ0,拒绝域——z≥zα;μ≥μ0,拒绝域——z≤-zα
而且,第一个拒绝域下标为2/α,后面2个下标为α(因为后面2个类似单侧置信区间)
σ2未知 – t检验

2个总体
σ12,σ22已知

σ12,σ22未知

成对数据

参数检验假设的步骤

方差假设检验
χ2检验法

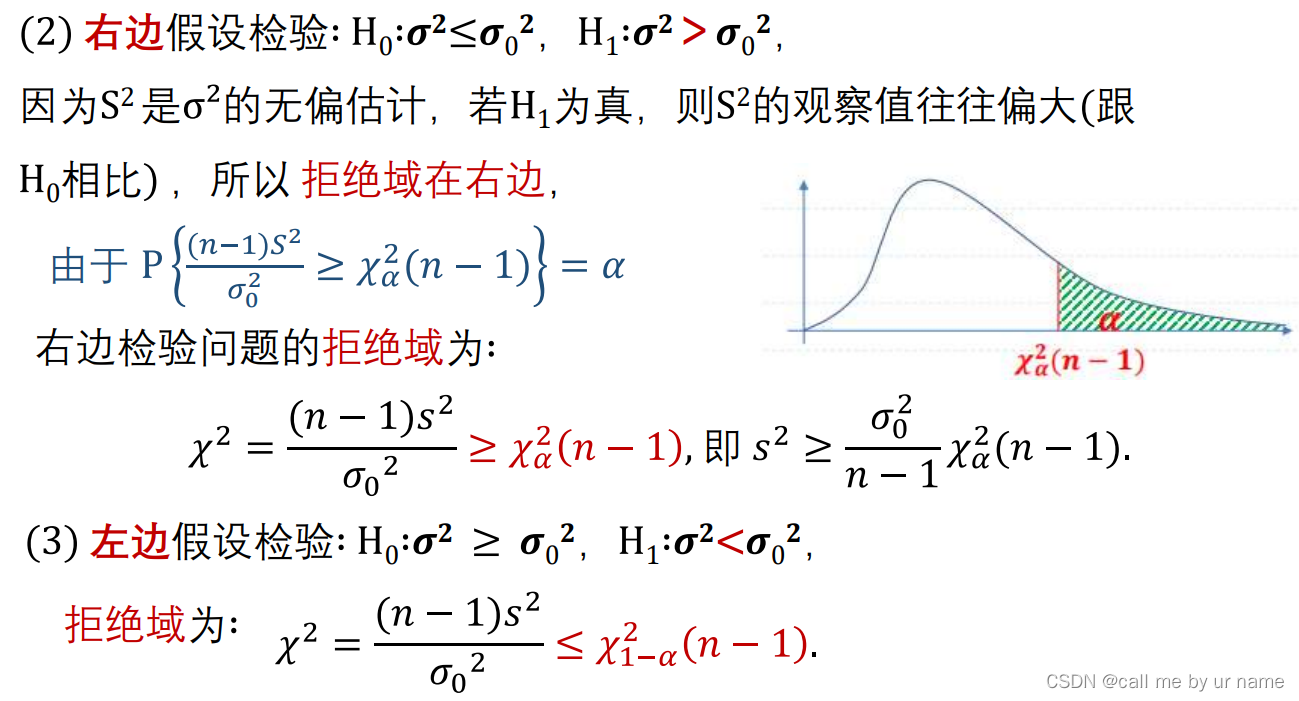
F检验法

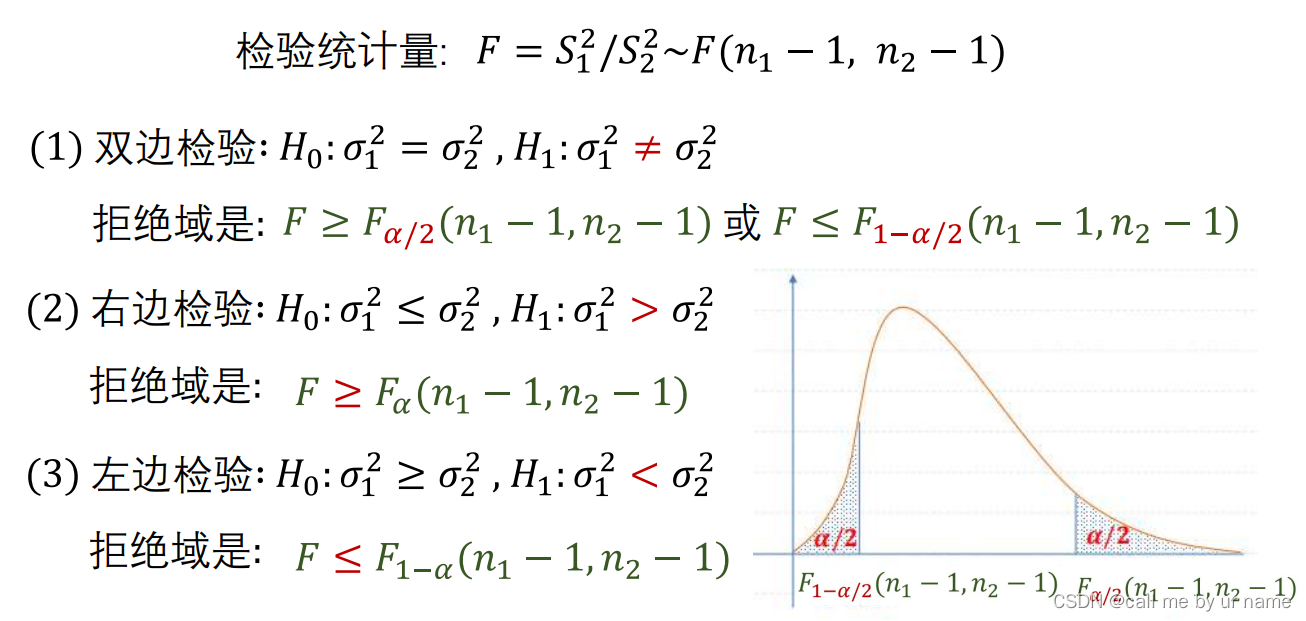
练习


这道题,不是一如既往地直接看题目设问,然后作出假设H0:μ>10(因为,会发现原假设一定带有等于号的(=,≤,≥),所以不能单纯用一个大于号)