目录
前言
概率
概率公式
贝叶斯公式
链式条件概率
例题
1. 求联合概率分布/边缘概率分布/条件概率分布
2. 灵活运用贝叶斯公式
概率总结
贝叶斯网络
判断独立性
两个事件独立的判断
条件独立性的判断
假设条件独立的链式法则
⚠Active / Inactive Paths 判断独立性
贝叶斯网络中的条件概率
编辑
多重连接和多重消除 Multiple Joins & Multiple Elimination
⚠作业题
前言
本复习笔记基于李晶晶老师的课堂PPT与复习大纲,供自己期末复习与学弟学妹参考用。
概率
概率公式
贝叶斯公式
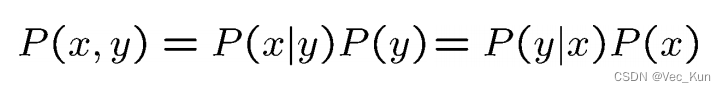
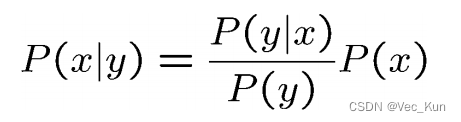
链式条件概率
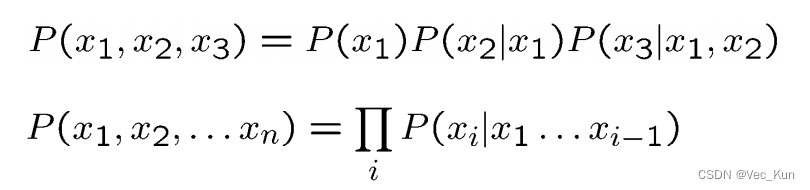
例题
1. 求联合概率分布/边缘概率分布/条件概率分布
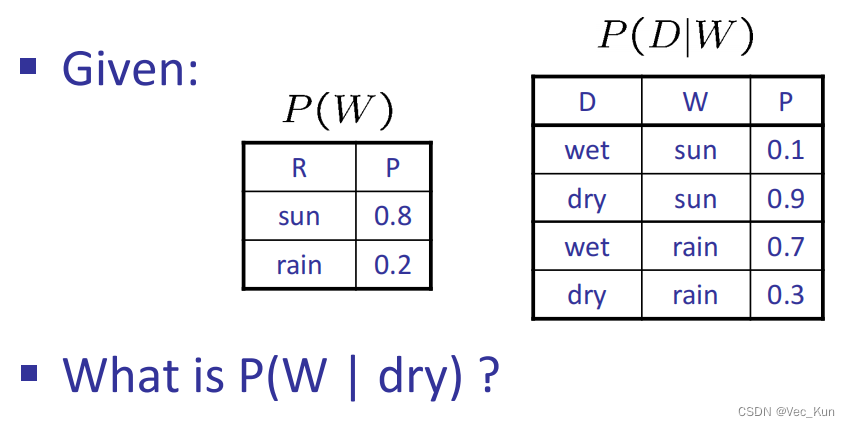
首先明确,P(W | dry)是一个概率分布,而不是一个概率值。不能写成 P(W | dry)=....
①求联合概率分布P(D,W);
②求边缘概率分布P(D);
③求条件概率分布P(W | D).
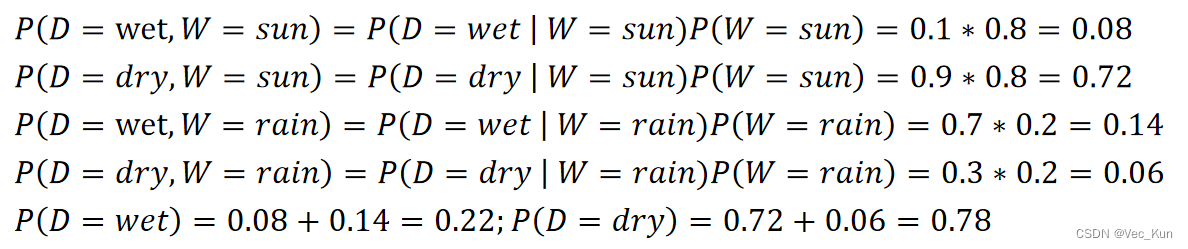
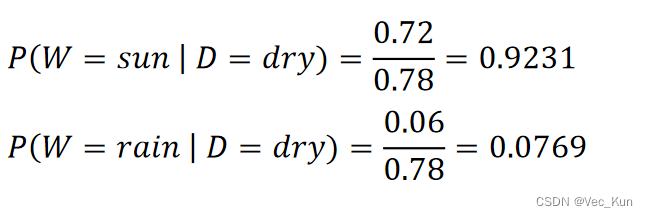
| P(W | dry) | ||
| D | W | P |
| dry | sun | 0.9231 |
| dry | rain | 0.0769 |
2. 灵活运用贝叶斯公式
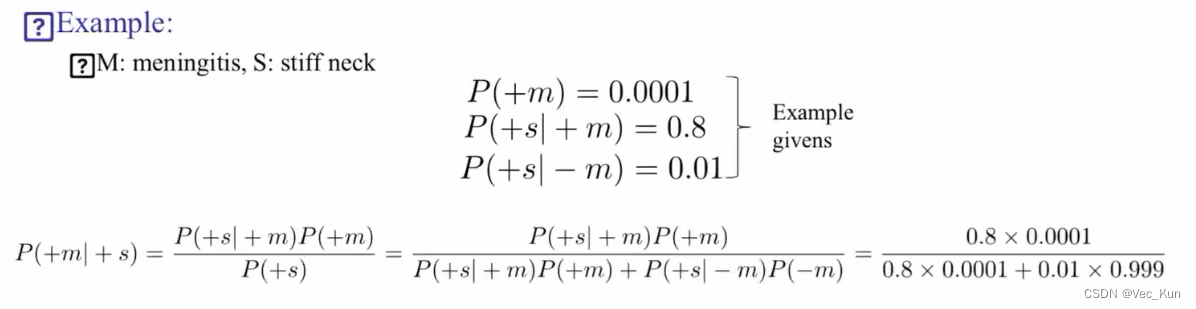
概率总结

贝叶斯网络
判断独立性
两个事件独立的判断
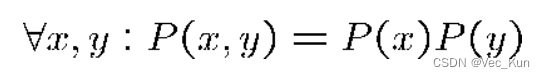
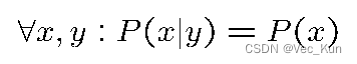
条件独立性的判断

假设条件独立的链式法则

⚠Active / Inactive Paths 判断独立性
要判断X,Y的独立性:
1. 找到X到Y的所有路径paths
2. 如果一个path的所有三元组都是active那么此path就是active
3. 若存在一个path为active,那么X、Y就是非独立的,反之独立
简言之:找到一条path的所有三元组都是active那么就非独立;
若只存在一条路径,那么找到一个inactive的三元组就独立,如果全部active才非独立。
⭐可以把X、Y理解为两个水池,如果有一根连通水管(path)里的开关全打开了(active)那么二者连通,不独立(independence);如果就只有一根水管连接,那么只要有一个开关被关闭(inactive)那么就独立。
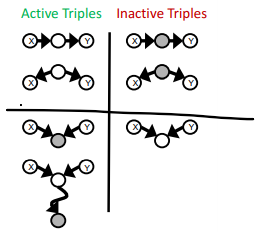
【上图阴影表示确定条件,即given。】
⭐只需要记间接因果(中间条件已知)、已知同因(父节点已知)、未知共果是active(子节点未知),其他三个对立的象限自己就出来了。
25-bn (washington.edu)
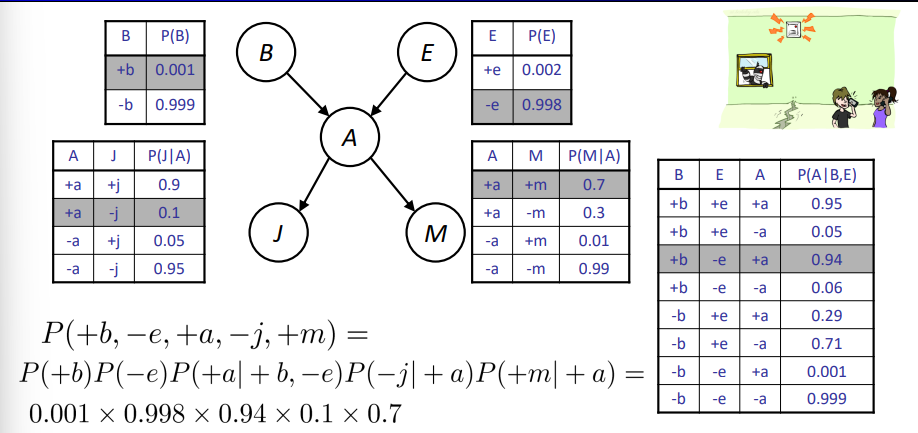
贝叶斯网络中的条件概率
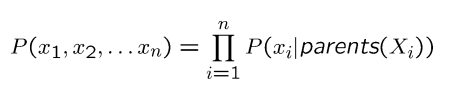
文字描述: 遍历每一项,分别以它们的父节点为条件,连乘即可。
举例说明比较直观:
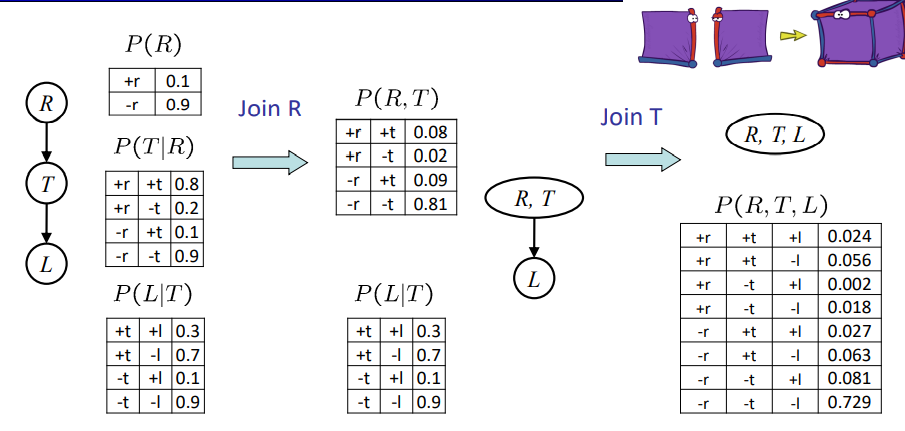
多重连接和多重消除 Multiple Joins & Multiple Elimination
对应乘起来就行了,没什么。

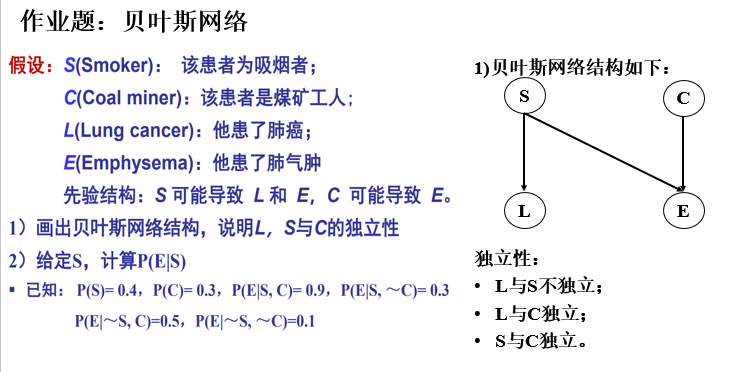
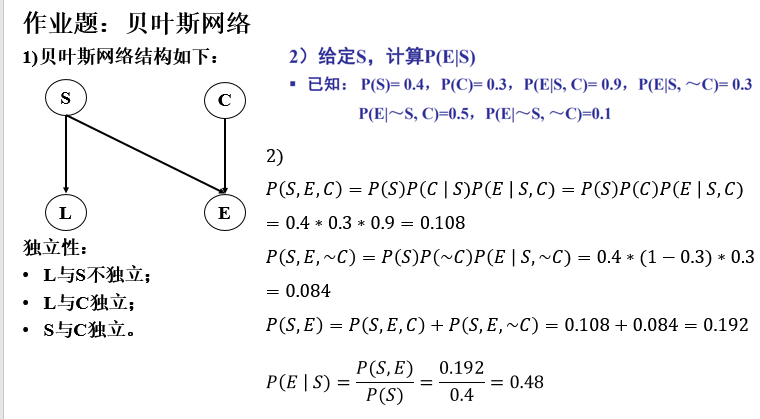
⚠作业题



![[DiceCTF 2023] rRabin](https://img-blog.csdnimg.cn/img_convert/c400e93ddc68fd032a3e8aeb7c634327.png)