LeetCode 62不同路径

题目讲解

思路

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

根据题意来看机器人只能进行向右和向下的移动，然后求有多少路径
这里的递推公式是

想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。

此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。

那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

所以这道题递推公式为 dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

class Solution {
    public int uniquePaths(int m, int n) {
         int dp[][]= new int[m][n];
         for(int i=0;i<m;i++)
         {
             dp[i][0]=1;
         }
         for(int j=0;j<n;j++)
         {
             dp[0][j]=1;
         }
         for( int i=1;i<m;i++)
         {
             for(int j=1;j<n;j++)
             {
                 dp[i][j]= dp[i-1][j]+dp[i][j-1];
             }
         }
         return dp[m-1][n-1];
    }
}

LeetCode 63 不同路径ii

题目讲解

思路

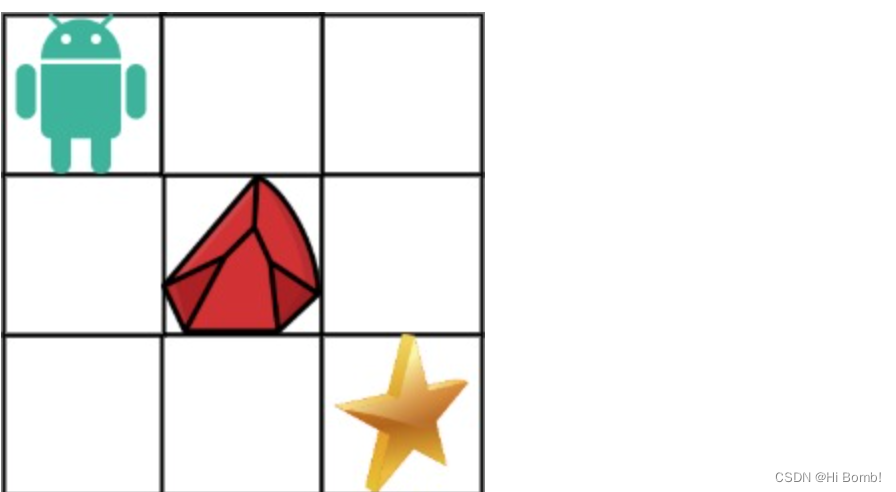
是上一道题的升级版有了障碍这一新的二维数组在这道题里是obastacleGrid
在递推公式上与上一题不同需要考虑到如果遇到障碍的情况但是大体是不变的

递推公式和62.不同路径一样，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

但这里需要注意一点，因为有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）。

if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候，再推导dp[i][j]
    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}

然后就是进行初始化

 for(int i=0;i<m&& obstacleGrid[i][0]==0;i++)
        {
            dp[i][0]=1;
        }
        for( int j=0;j<n&& obstacleGrid[0][j]==0;j++)
        {
            dp[0][j]=1;
        }

与上道题不同，遇到障碍

但如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。

最后从正面进行遍历，然后在记得打印

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m =obstacleGrid.length;
        int n= obstacleGrid[0].length;
        int [][]dp= new int[m][n];
        if( (obstacleGrid[m-1][n-1]==1)||(obstacleGrid[0][0]==1 )) return 0;
        for(int i=0;i<m&& obstacleGrid[i][0]==0;i++)
        {
            dp[i][0]=1;
        }
        for( int j=0;j<n&& obstacleGrid[0][j]==0;j++)
        {
            dp[0][j]=1;
        }
        for( int i=1;i<m;i++)
        {
            for( int j=1;j<n;j++)
            {
                dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
            }
        }
        return dp[m-1][n-1];
    }
}