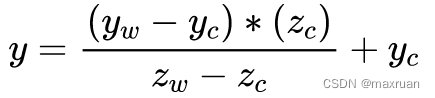1 、正向投影: 世界坐标系到像素坐标系
世界3D坐标系(x, y, z) 到图像像素坐标(u,v)的映射过程
(1)世界坐标系到相机坐标系的映射。
两个坐标系的转换比较简单,就是旋转矩阵 + 平移矩阵,旋转矩阵则是绕X, Y,Z 轴旋转获得。
R 属于世界坐标系到相机坐标系的旋转矩阵, 旋转矩阵为R = R(z) * R(y) * R(x),
具体根据相机外参标定时规定的旋转方向来定,为 3 × 3 矩。
t 为世界坐标系原点到相机坐标系原点的平移矩阵,为3 x 1 矩阵。
世界坐标到相机坐标的映射为:
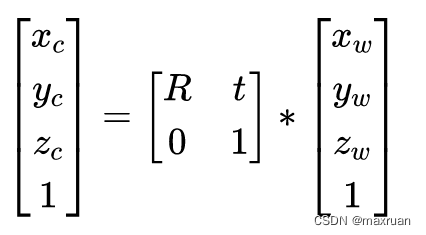
(2)相机坐标系内归一化坐标平面
射线到平面上的投影都是等效的,因此进行归一化,方便计算。
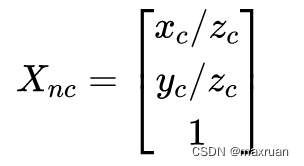
(3)归一化平面上发生畸变
畸变分为径向畸变(光线折射)和切向畸变(安装倾斜)。
联立径向畸变和切向畸变公式,得到畸变模型 distortion() 为:
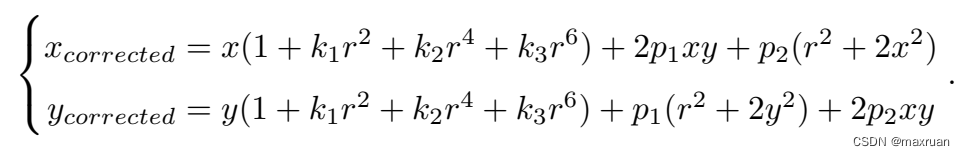
对应到标定文件中的畸变参数为。
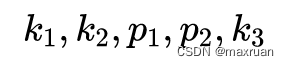
即畸变映射为:
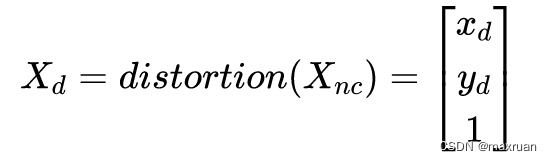
(3)归一化平面坐标到像素平面
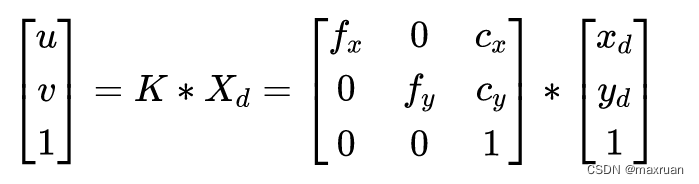
1 、反投影: 像素坐标系到世界坐标系(Z = 0)平面
图像像素坐标(u,v)到世界3D坐标系(x, y, z = 0) 的映射过程
(1)像素平面到归一化平面
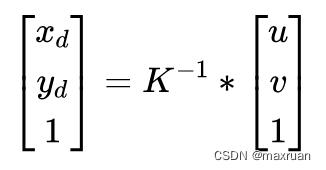
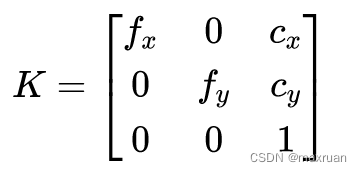
(2)归一化平面上逆向去畸变
由于像素坐标(u, v)是畸变后的点经过内参映射得到。因此需要将畸变点逆向去畸变为非畸变点。
牛顿迭代法:
初始化:
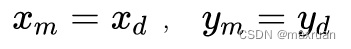
迭代求解:
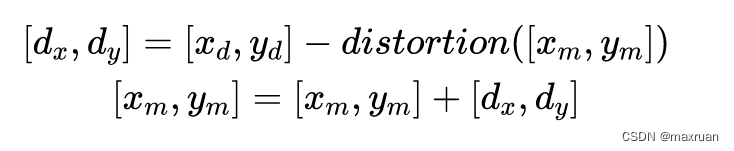
直到误差足够小,得到非畸变点
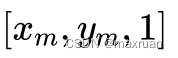
到此获得相机坐标系下归一化平面上的点。
(2)相机坐标系归一化平面到地平面映射
从相机坐标系的一个平面到世界坐标系的另一个平面的映射通过单应矩阵H可以得到。
假设相机坐标在世界坐标系下为(xc, yc, zc),
将相机坐标下归一化平面点旋转后平移到世界坐标系下:
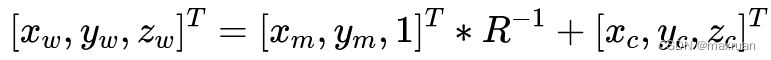
假设映射到世界坐标系下地平面上的点为(x, y, 0), 则根据相似三角形:
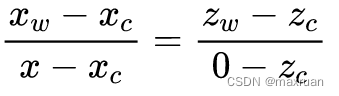
求得:
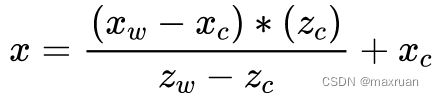
同理: