这好像是一个哲学问题。
目录
前言
一、顺序点是什么?
二、发生有关顺序点的问题代码
vs中:
gcc中:
三、细读汇编
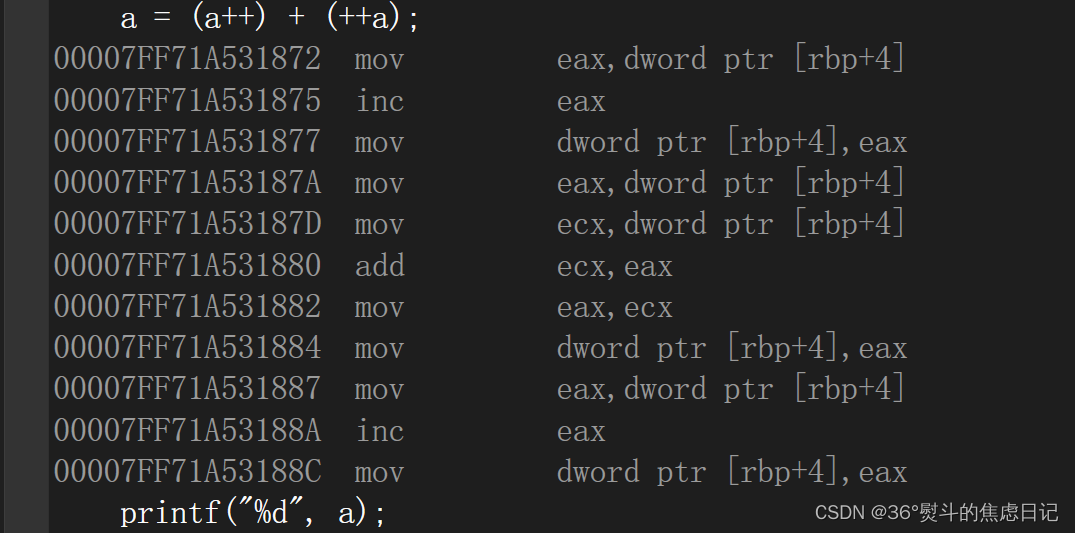
1.vs汇编如下(示例):
2.gcc汇编如下(示例):
四、理解汇编
图解
原因:
五、如果是a = (++a) + (++a)呢?
1.vs汇编:
2.图解:
总结
前言
一旦执行到一个顺序点,此前的副作用都必须生效。
一、顺序点是什么?
顺序点,也称作序列点,是计算机程序中一些执行点,在该点处之前的求值的所有的副作用已经发生,在它之后的求值的所有副作用仍未开始。在C与C++程序设计语言中,表达式的值依赖于它的子表达式的求值顺序。增加更多的顺序点限制了可能的求值顺序,能保证有一个一致结果。(来源:百度百科)
二、发生有关顺序点的问题代码
代码如下(示例):
#include <stdio.h>
int main()
{
int a = 0;
a = (a++) + (++a);
printf("%d", a);
return 0;
}a++的副作用是将a增加了a,按照以往的常识是在这句话结束后才会产生此副作用,但是这时表达式左边也是a,a到底是在这句话结束后才产生的副作用还是一边向后执行,一边产生副作用?(哲学吗)
这个就取决于编译器了,这也正是这段代码的问题所在。
vs中:
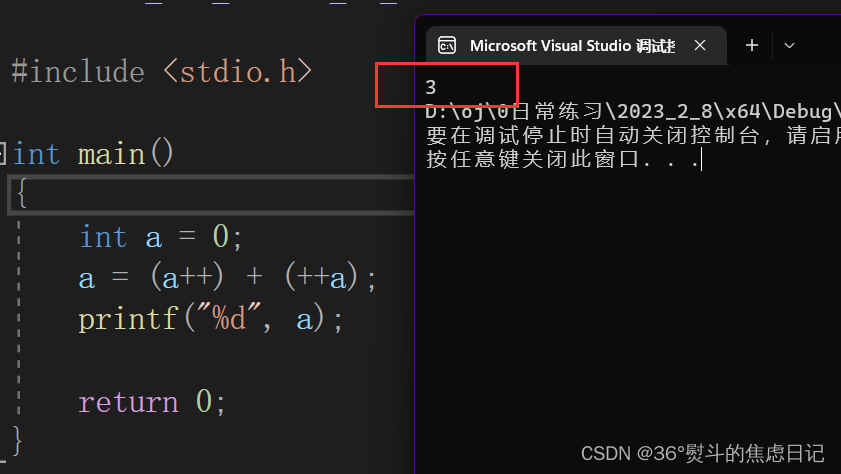
gcc中:

三、细读汇编
1.vs汇编如下(示例):
2.gcc汇编如下(示例):
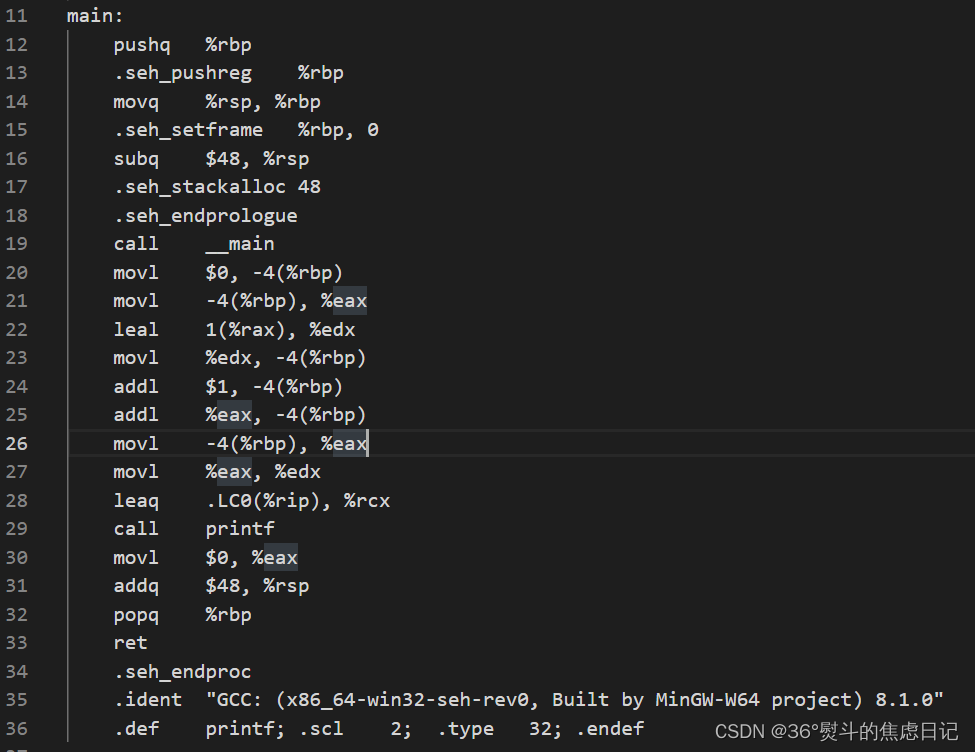
四、理解汇编
汇编的人话版就是:
①前置++优先级略高于后置++,先算前置的,
②算出来以后因为表达式左边也有a,前置++这个式子对于其有副作用,就去更新左值a,a = 1
③更新好后,再来计算a++
④因为后置++是先赋值后计算,所以在后置++中,a是前置++算出来以后的值,所以计算后置++后,a没有发生变化,不用更新a(a = 1)
⑤两个++都算完以后,该算“+”了,此时计算的式子是:1+1 = 2;2是表达式右边的值,其等于表达式左边,左边是a,所以此时a = 2
⑥此时该后置++运算了,取得a的最新值为2,进行++,得到a的最终值是3。
图解
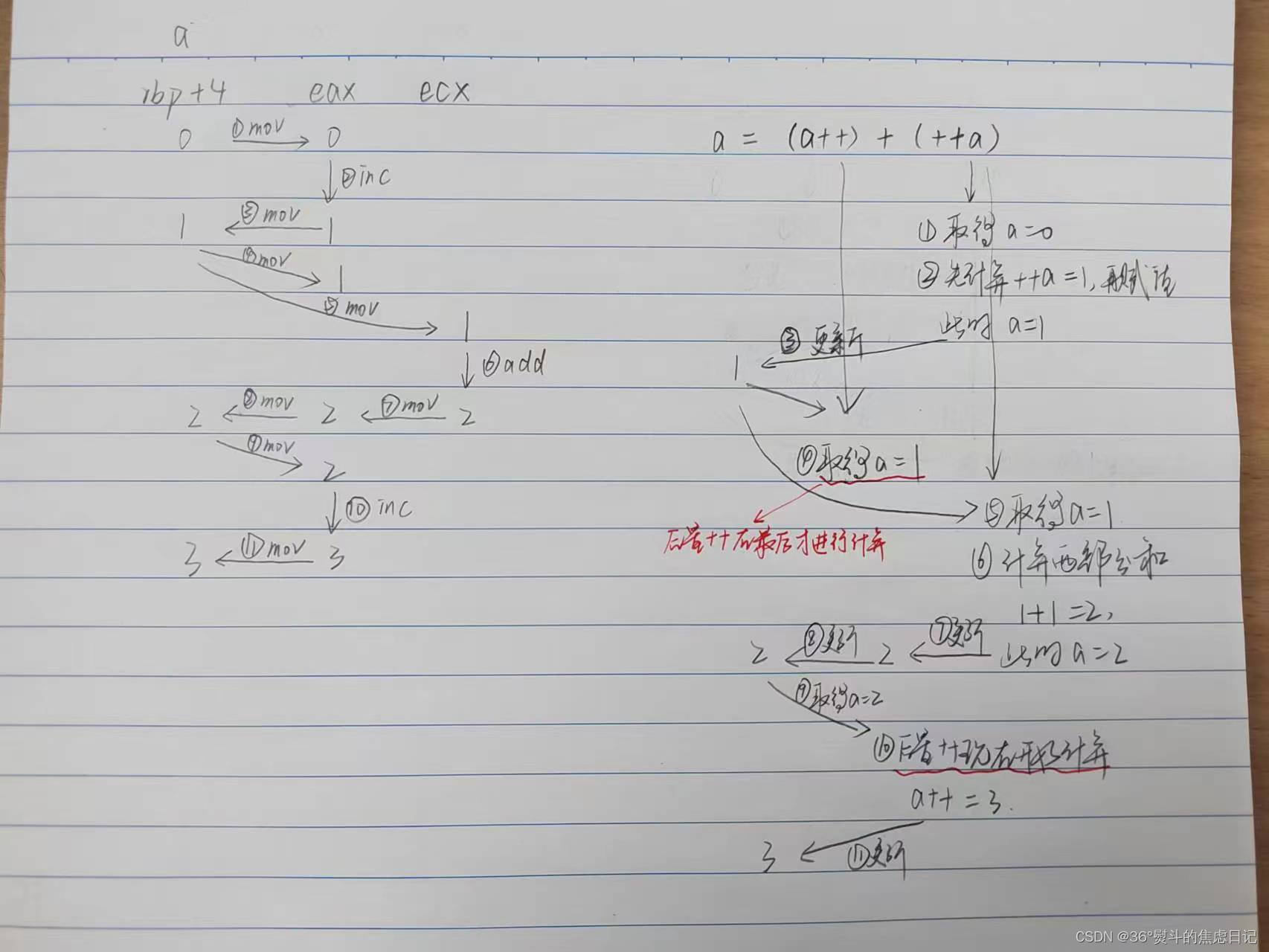
原因:
所以,当有副作用式子出现时,如果还写了一段问题代码,那么这个时候就需要看编译器对于顺序点前后的处理方式,vs与gcc也正是因此而产生的不同答案。
五、如果是a = (++a) + (++a)呢?
与四分析方式相同,结论是:
先算出所有的副作用带来的影响(++),再计算没有副作用的式子(+)。
1.vs汇编:
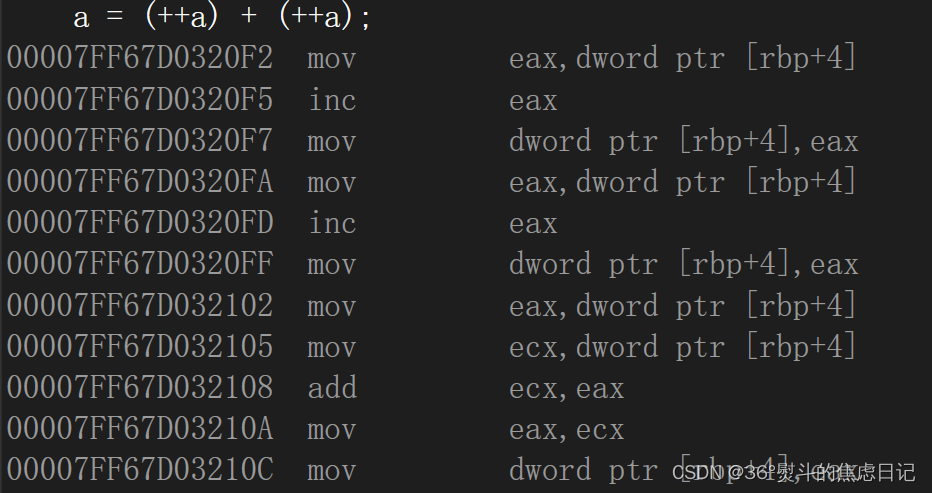
2.图解:

总结
- 表达式如果不能通过操作符的属性确定唯一的计算路径,表达式就是存在问题的。
- 尽量少写产生顺序点疑问的代码。