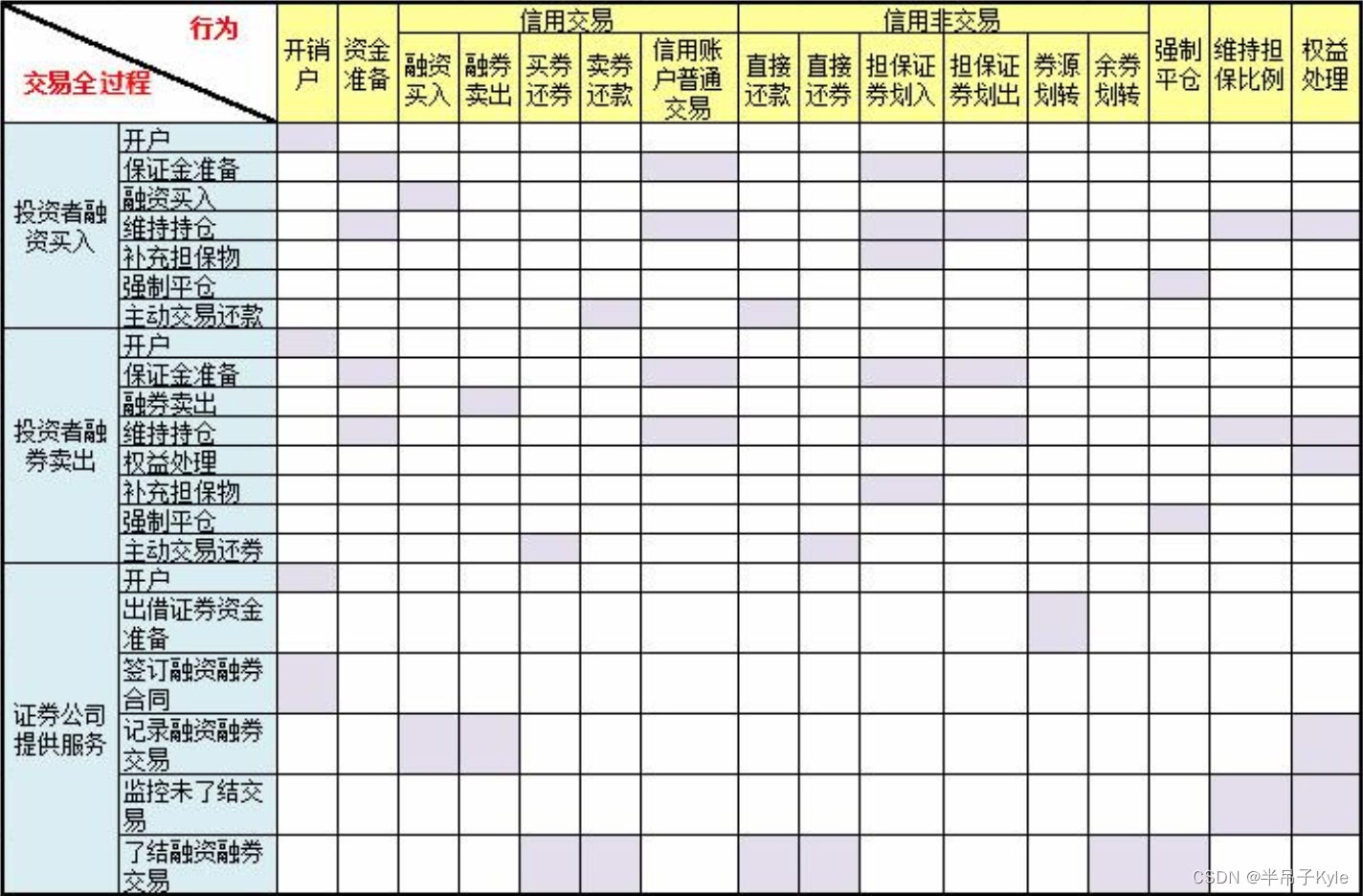
1.通过集合相等来讲解什么是映射关系

上面问的这个问题（2N+ = N2）说明了什么？

——两个无穷集合，如果能找到一种对应关系（映射关系），那么我们就可以说这两个集合是等价的。

  数列的极限就是趋势

极限就是无限接近，但是不等于

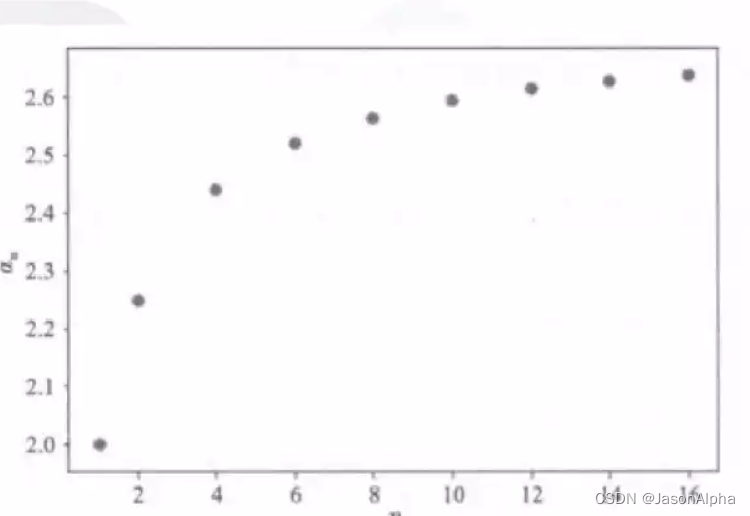
下面这是一个数列的极限，当n趋近于正无穷，数列趋近于自然数e

用画图表示就是这样，无限逼近于自然数e

 洛必达法则

若函数f(x)和g(x)满足下列条件:

随着x逼近a, 本身f(x)和g(x)都是逼近于正无穷的，但是通过f(x)和g(x)做比，可以得出这个“比”趋近于某个数A。如果A大于1，比如说A等于2，说明f(x)比g(x)趋近于正无穷的速度快。A表示的是一种趋近速度。

        （1）随着x不断向a逼近，如果f(x)和g(x)是趋近于一个常数，那么A越大，f(x)的收敛速度越快。

        （2）随着x不断向a逼近，如果f(x)和g(x)趋近于无穷，那么A越大，f(x)发散的速度越快

 像我们做机器学习追求的就是“单调有界收敛”，像下面这个图，

        单调：从小于e到逼近e这个方向走，说明这个数据是有规律的。如果方向一会增，一会减就是无规律的，就是噪声。

        有界：收敛的过程中，走了一段时间，和e的差距小于某个值，epsilon，比如0.1

和单调有界收敛相反的是“无界发散”，其实就是噪声

夹逼准则

假设一个函数是c，这个c介于a和b之间。这个函数c的极限不好求，我去求c所在区间的两个端点的极限值，进而推出c的极限值。这个过程可以叫做双参设计

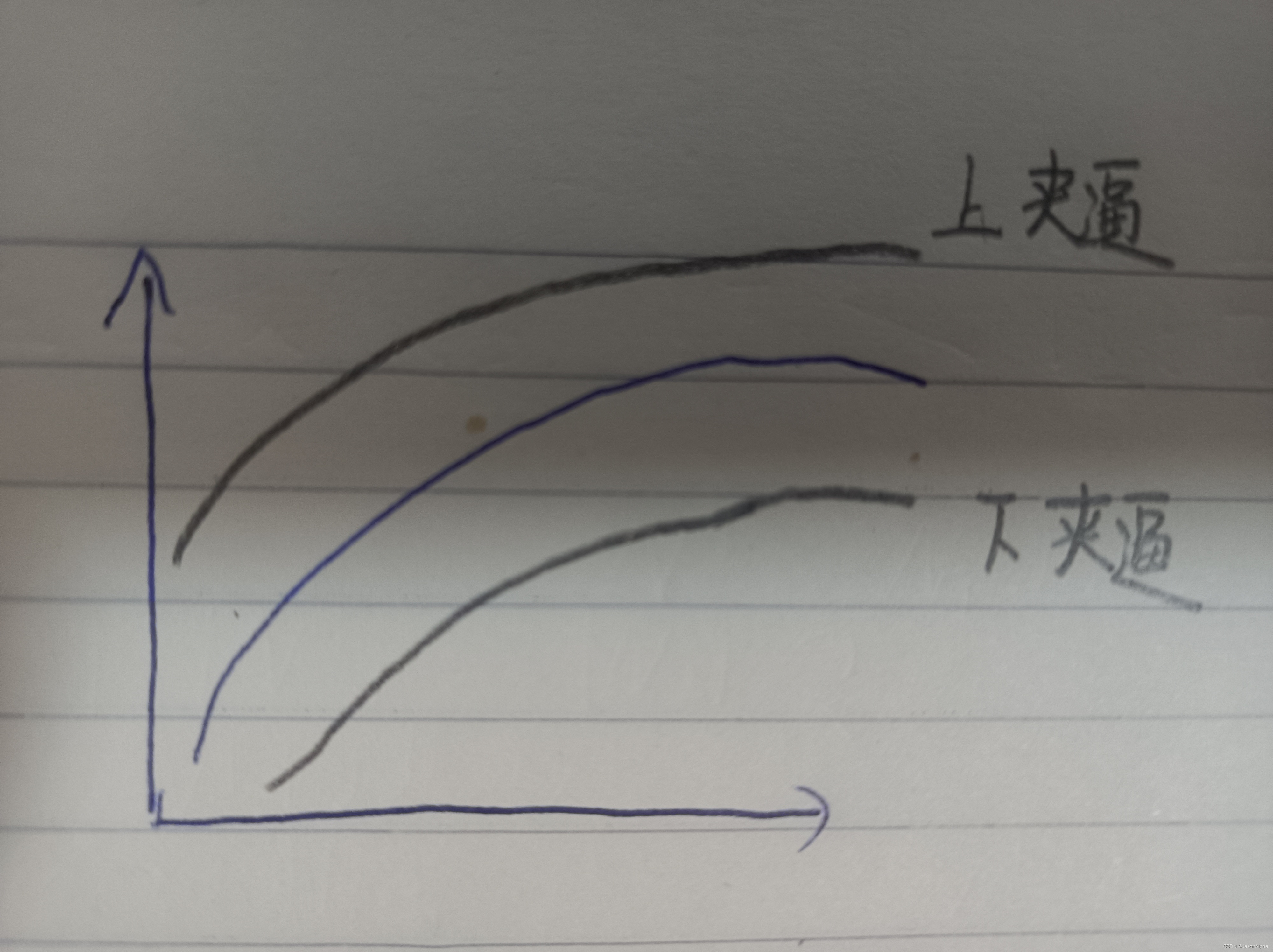
 上夹逼趋近于c,下夹逼也趋近于c。上夹逼和下夹逼不断逼近c,离c越来越近，直到我们找到上夹逼或者下夹逼中的一个更加贴近c，我们就把这个夹逼拿出来作为c的近似函数。这个无限接近的过程就是我们所所的“拟合“。

        过拟合就是上夹逼和下夹逼趋近到最中间了（我认为不对）

        欠拟合就是，上下夹逼距离我们的的拟合目标c距离太远了。

函数的极限

什么是函数？

函数表达式 是为了以数学符号的形式 表示函数图像。

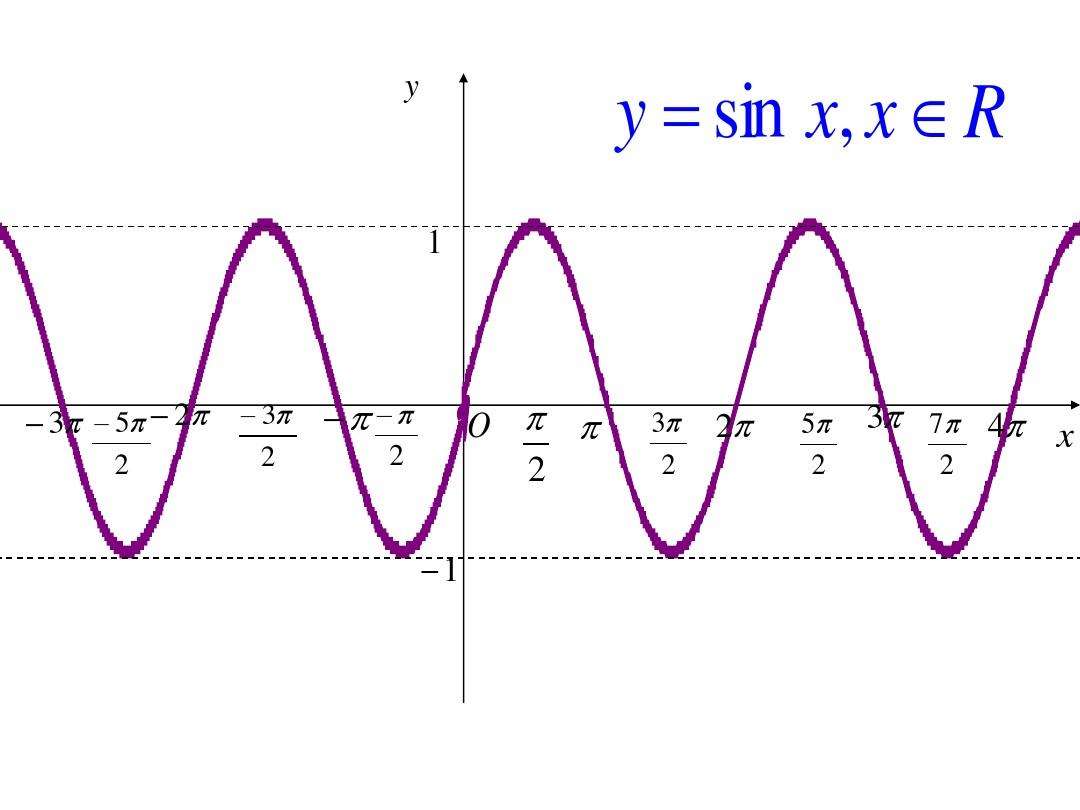
函数起源于信号学里面的函数图像。（1）比如一个函数图像像下面这样，每一次我们给别人说我们讨论一下下面这样的一个函数的时候，我们都得把这个函数的图像画一遍。每次都要画图真的很累，于是这帮专家发现我们可以用sin(x)这样一个简单的函数表达式来表示下面这张图，所以才有了函数表达式的广泛应用。（2）只有把函数图像转换成数学表达式以后，就可以使用丰富多彩的数学工具，运用过去数学家积累的一些定理和推论。单单拿过一张函数图像，我们是没有工具来处理和分析的。

函数的间断点

一个连续的函数，它一直走，走着走着，到一个点，它忽然断了，后面有继续连续走下去。对于这种间断点，我们该如何处理呢？

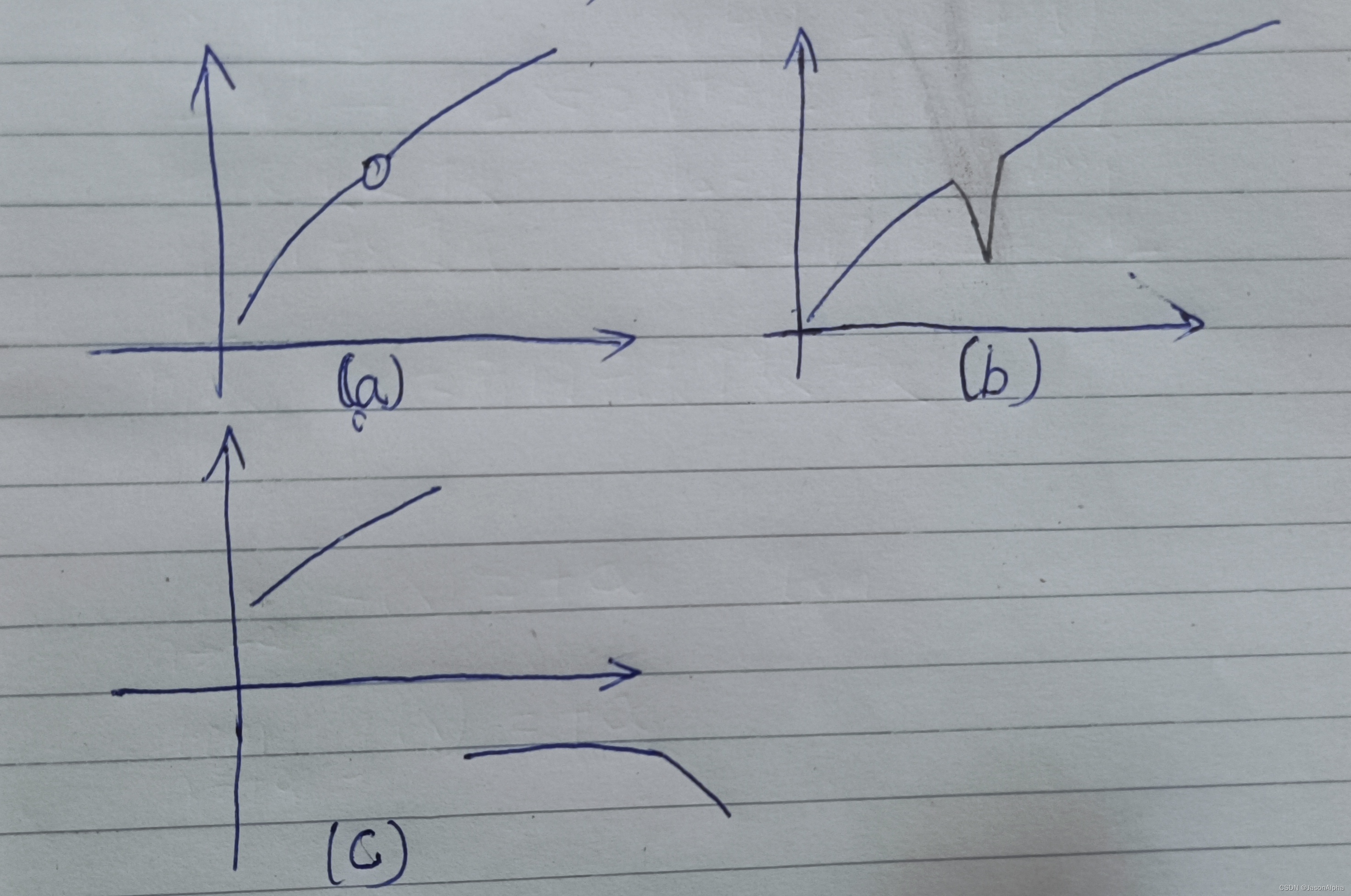
（a）这个间断点叫缺失值。因为他是和左右两侧的趋势是相同的。这种情况，如何填充这个缺失值呢？让这个点继续保持左右两点的趋势，就得出缺失值的预测值了。

（b）缺失的值是异常值outlier。这个值反映不出整体趋势，应该舍弃掉这个值，否则会影响到我们模型对于数据的拟合。

（c）这种间断，间断的两侧，属于不同的cluster。这种数据，适合用聚类。

因此我们得出结论，如果数据能够保持连续、没有间断点的话，它的泛化能力很大可能性是不错的（比如上面这个b情况，这种有间断点的情况，如果把间断点再引入进来，训练出来模型泛化性就不好）

介值定理

        介值定理的定义：如果定义域为[a，b]的连续函数f，那么在区间内的某个点，它可以在f（a）和f（b）之间取任何值，也就是说，介值定理是在连续函数的一个区间内的函数值肯定介于最大值和最小值之间。

        我的理解：：对于定义域为[a,b]的连续函数f。我们可以拿到函数f的最大值最小值。对于函数值y介于这个最大值和这个最小值之间，一定发 能找到至少一个对应的自变量x的取值范围介于[a,b]之间。

利普希茨连续性

 这个性质将（a-b）这个问题，转换成了f(a)-f(b)的问题。f(a)-f(b)始终"小于等于"K(a-b)体现的就是f(a-b)逼近K(a-b).

我们可以把利普西斯连续性的公式移项，得到上面这个式子。我们可以发现，K|a-b|是我们的目标|f(a) - f(b)|无限的逼近于K|a - b|。实际上这个逼近的程度，可以用0这么小，我们自己是可以调整的,比如小于，比如0.1,0.01这样一个人为可控的小量。

---

本文来自于，笔者收听“点头教育”的课程《机器学习数学基础》过程中记录的笔记。为了尊重教学视频的版权，这里列举一下点头教育的联系方式。

点头教育官网：

https://www.diantouedu.cn/index

《机器学习数学基础》